Ортогональные ЦКП второго порядка

Ортогональным планом называется такой, у которого матрица планирования X строится так, чтобы матрица С = Х^ТХ оказалась диагональной. Используем этот подход и при построении планов второго порядка. План называется центральным, если все точки расположены симметрично относительно центра плана. ОЦКП — центральный симметричный ортогональный композиционный план.

В ОЦКП входят: ядро — план ПФЭ с JV₀ = 2″ точками плана (табл. 4.3), п₀ (одна для этого плана) центральная точка плана (х, = 0, i = 1, …, п) и по две «звездные» точки для каждого фактора.

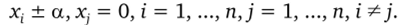
При этом в каждой плоскости, содержащей ось Y и координатную ось i-го фактора (проходящей через центр плана), оказываются три значения фактора х₍ (-а, 0, +а) и три соответствующих значения у.

Общее количество точек в плане ОЦКП составляет.

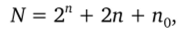
где для ОЦКП п₀ = 1. При п > 2 в ОЦКП оказывается меньшее количество точек, чем в плане ПФЭ 3″ (рис. 4.2).

Для ортогонального плана необходимо, чтобы выполнялось соотношение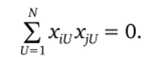

Таблица 4.3. Число точек в плане.

Рис. 4.2. ОЦКП при п = 3.

Так как х_ои = 1, то для столбцов; = 1, 2, т + 1 должно выполняться условие.

означающее необходимость выполнения требования, чтобы сумма элементов любого столбца (кроме j = 0), включая столбцы, соответствующие квадратам фактора, должна быть равна нулю. Это возможно, если члены столбцов, соответствующих квадратам факторов, преобразованы, иначе сумма квадратов факторов не может быть равна нулю.

Преобразование элементов этих столбцов осуществляется в виде.

где а — величина, зависящая от числа факторов.

Сумма элементов столбца, соответствующего квадратам факторов,.

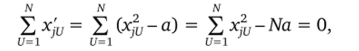
N.

5>_;²и и=1.

откуда a = .

В общем случае ортогональный центрально-композиционный план при трех (п) факторах представлен в табл. 4.4.

В ОЦКП каждый фактор фиксируется в общем случае на пяти уровнях (-а, -1, 0, 1, +а).

Для определения неизвестных, а и, а нужно сформировать и решить систему из двух уравнений. Одно из них для а мы записали ранее. Другое уравнение получим из условия ортогональности для столбцов х'_Аих'₅:

После простейших преобразований с учетом того, что N = N₀ + 2п + п₀ — общее число опытов в плане, получаем соотношение.

Соотношение для а при j = 1, 2 или 3 может быть записано как.

Подставив его в последнее уравнение, получаем.

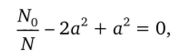
откуда константа преобразования.

Тогда.

и плечо «звездных» точек.

Например, для ОЦКП (табл. 4.5) при числе факторов п = 3 имеем следующие параметры плана:

Таблица 4.5. Параметры ОЦКП при трех факторах.

Очевидно, что план является ортогональным. В отличие от планов ПФЭ для ОЦКП сумма квадратов факторов разных столбцов не является одинаковой.

По результатам опытов плана формируется полином.

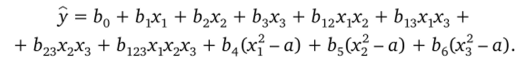
Коэффициенты полинома Ь₀, Ь_г, b₂, b₃, Ь₁₂, Ь₁₃, Ь₂₃, Ь₁₂₃, Ь_А, Ь₅, Ь₆ определяются как.

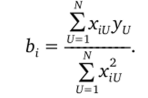
4.5. Ортогональные ЦКП второго порядка Можно преобразовать полином к виду.

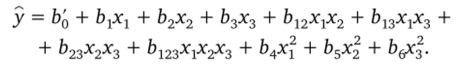
где ?>о ⁼ Ь₀~ Ь₄а + Ь₅а — Ь₆а.

Значения параметров ОЦКП при произвольном числе факторов представлены в табл. 4.6.

Таблица 4.6. Значения параметров ОЦКП при числе факторов п.

При п = 2 ОЦКП совпадает с планом ПФЭ 2³. «Звездные» точки ОЦКП в этом случае лежат на границах варьирования факторов. Если точки плана ПФЭ 2^П всегда лежат на окружности (поверхности шара, гипершара), то точки плана ОЦКП не лежат на какой-либо одной окружности (поверхности шара, гипершара). План ОЦКП не является насыщенным. Так, например, для п = 3 полином имеет 11 членов со своими коэффициентами, но для их определения используются пятнадцать опытов.

Пример 4.1.

Пример построения плана ОЦКП для п = 2.

Параметры плана N₀ = 4, N = 9, а = 1, а = 2/3, 1 — а = 1/3, -а = -2/3, а² — а = -2/3 (табл. 4.7).

Использован рассмотренный ранее план ПФЭ 2² с добавленными опытами 5—9.

Коэффициенты полинома.

Таблица 4.7. Параметры плана.

N₀ = 4, N = 9, а = 1, а = 2/3, 1 -а = 1/3, -а = -2/3, а²-а = -2/3.

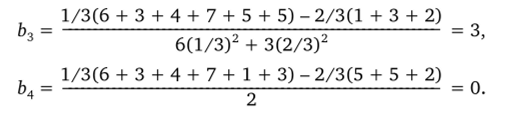
Полином принимает вид.

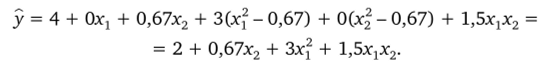
(Ранее по плану ПФЭ 2² был сформирован полином у = 5 + + 0,5jc₂ + 1,5*,*₂);

Рассчитанные значения у по полиному приведены в плане, как и величины у_и — _у_и|, подтверждающие достаточно высокую точность полинома. Так, в центральной точке плана, в отличие от случая применения плана ПФЭ 2², расхождений нет.