Примеры решения задач

Пример 3.1. Определим осевой и центробежный моменты инерции для характерных осей прямоугольника (рис. 3.4).

Решение. Момент инерции относительно оси Ох определяется согласно формуле (3.9) интегрированием:

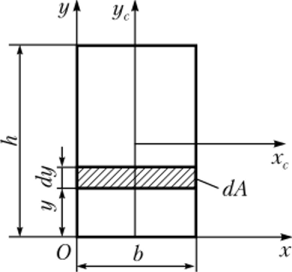
Рис. 3.4. К примеру 3.1.

откуда получим формулу.

С использованием первой формулы (3.17) получим формулу для момента инерции относительно центральной оси:

Окончательно получаем.

Аналогично получаются формулы для моментов инерции относительно осей У и У_с'-

Так как х_с и у_с — главные оси, центробежный момент инерции относительно этих осей равен нулю. Используя формулу (3.19), вычислим значение центробежного момента инерции относительно осей х и у:

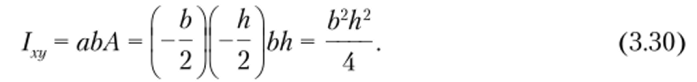
Пример 3.2. Рассмотрим фигуру, имеющую форму прямоугольного треугольника (рис. 3.5). Определим значения ее геометрических характеристик.

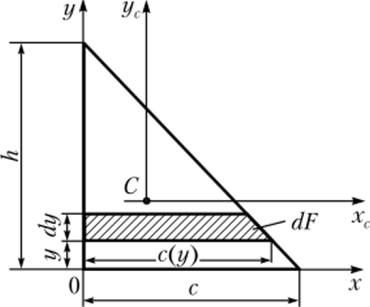
Рис. 3.5. К примеру 3.2.

Решение. Начнем с определения момента инерции фигуры относительно оси х:

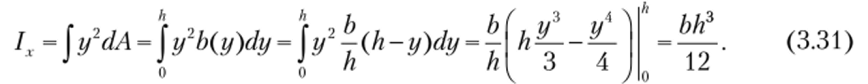
Для определения момента инерции относительно оси используем первую формулу (3.17):

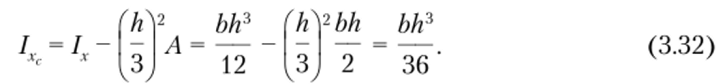
Аналогично получаются моменты инерции относительно осей у и у_с:

Определим центробежный момент инерции относительно осей х и у. Для этого заранее определим эту величину для дифференциала площади:

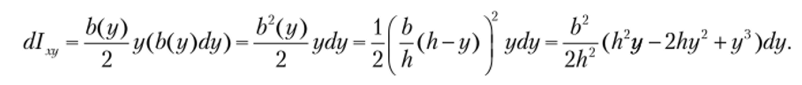
Далее интегрированием получим значение центробежного момента инерции для треугольника:

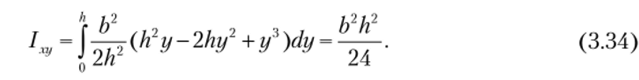
Для определения центробежного момента инерции относительно центральных осей х_с и у_с используем формулу (3.19):

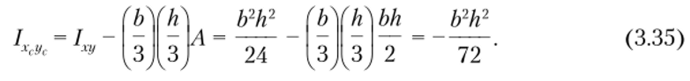
Пример 3.3. Определим полярный и осевые моменты инерций для фигуры, которая имеет круговую форму (рис. 3.6).

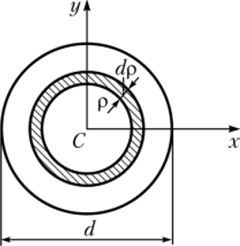
Рис. 3.6. К примеру 3.3.

Решение. Для определения значения полярного момента инерции используем формулу (3.10). Бесконечно малый элемент площади представим как площадь кольцевой фигуры, имеющей ширину dp и длину 2лр (см. рис. 3.6), площадь которой dA = 2npdp учтем в формуле (3.10). При этом в результате интегрирования получим.

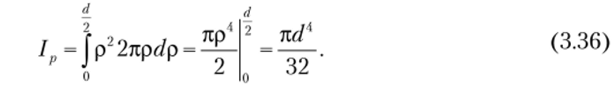
Если учесть, что осевые моменты относительно осей х и у равны друг другу (I_x = IX то согласно формуле (3.11) получим.

Определим для фигуры полярный статический момент в соответствии с формулой (3.8):

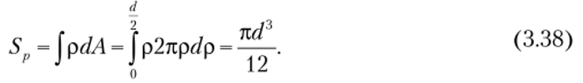
Пример 3.4. Определим полярный и осевые моменты инерции для кольца (рис. 3.7).

Рис. 3.7. К примеру 3.4.

Решение. Бесконечно малая площадь и интеграл запишутся аналогично записи в предыдущем примере. Изменится только значение нижнего предела интеграла:

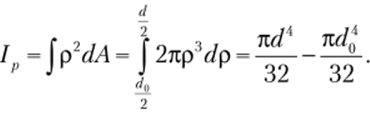
d₀

Введем обозначение с = —. В этом случае полярный момент инерции запишет;

а

ся в следующем виде:

Осевые моменты инерции аналогично предыдущей задаче равны друг другу. Поэтому согласно формуле (3.11) получим.

Определим полярный статический момент инерции:

Пример 3.5. Определим главные центральные моменты инерции полукруга (рис. 3.8).

Решение. Ось у является как осью симметрии, так и главной центральной осью, относительно которой момент инерции равен половине осевого момента полного круга.

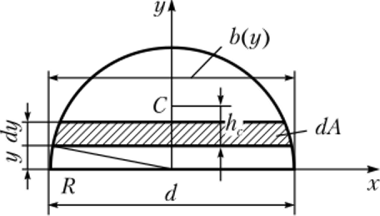
Рис. 3.8. К примеру 3.5.

С учетом формулы (3.37) определим эту величину:

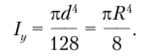
Найдем координату центра тяжести h_c полукруга (см. рис. 3.8). Для этого предварительно определим статический момент инерции фигуры относительно оси х:

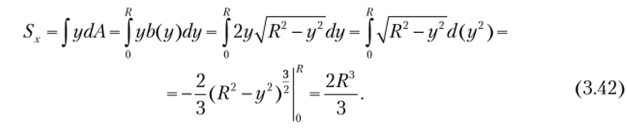
Площадь фигуры равна А = С помощью формулы (3.3) установим ординату центра тяжести:

Момент инерции относительно оси х_г определяется с помощью первой формулы (3.17):

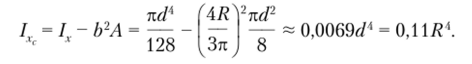
Пример 3.6. Для фигуры, представленной на рис. 3.9, определим положение главных центральных осей и моменты инерции относительно этих осей.

Рис. 3.9. К примеру 3.6.

Решение. Заданную фигуру представим как составную в виде двух прямоугольников. Согласно формулам (3.7) определим координаты центра тяжести составной фигуры:

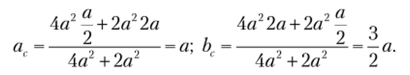
Опрсделим центральные осевые моменты инерции составного сечения:

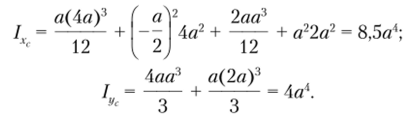
Вычислим значение центробежного момента инерции составной фигуры относительно центральных осей х_с и у_с

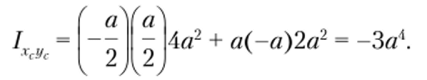
Положение главных центральных осей определим с помощью формулы (3.24):

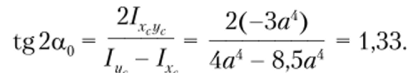
Из этого следует значение угла, который первая главная ось составляет с осью х_с: а₀ = 2б°30'.

Вторая главная ось перпендикулярна первой главной оси. Используя формулу (3.25), определим значения главных центральных моментов инерции фигуры:

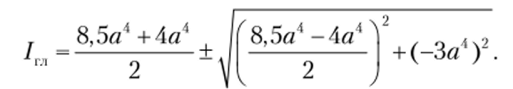
Окончательно получим максимальное и минимальное значения моментов инерции относительно центральных главных осей: I = 10а⁴; 7? = 2,5а⁴.

Пример 3.7. Составное сечение составлено из двух профилей (рис. 3.10): швеллера № 8 и двутавра № 10. Определим положение центра тяжести сечения и величину момента инерции сечения относительно центральной горизонтальной оси.

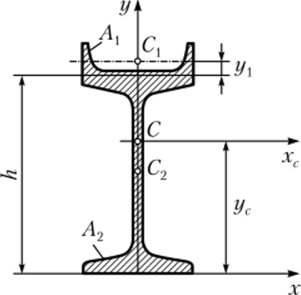
Рис. 3.10. К примеру 3.7

Решение. Для проведения расчетов используются данные таблиц соответствующих стандартных профилей, с помощью которых определяются необходимые для расчетов величины.

а) Швеллерный профиль № 8 (ГОСТ 8240—89)¹:

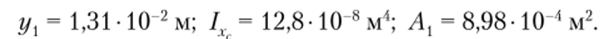
б) Двутавровый профиль № 10 (ГОСТ 8239−89)²:

Определим ординату центра тяжести сечения:

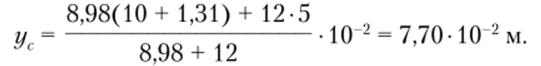
Определим величину центрального осевого главного момента инерции:

ГОСТ 8240–89. Сталь горячекатаная. Швеллеры с уклоном внутренних граней полок.

ГОСТ 8239–89. Сталь горячекатаная. Балки двутавровые.