Получение оценок дисперсий и выводов о степени влияния фактора

Если верна гипотеза о том, что влияние фактора х на целевую функцию у незначительно (несущественно), тогда разница между средними уровнями у' и у" будет также незначительной. Тогда оценка общей дисперсии 5ц{у} относительно общего среднего у и любая оценка дисперсии s_AJ{y} относительно группового среднего y_t (или усредненная оценка дисперсии s^{y} по всем;-м уровням:; = 1, 2,…, и) при JV —? °о будут стремиться к одному и тому же пределу, так как при этом любая ;'-я серия измерений может рассматриваться как представительная выборка из общей (генеральной) совокупности. В этом случае можно рассматривать три оценки генеральной дисперсии воспроизводимости о²{е} = ст²{у}, которая характеризует силу влияния помех е (ошибок эксперимента):

1. Несмещенную оценку дисперсии воспроизводимости, вычисленную по всем N наблюдениям (по всем и сериям).

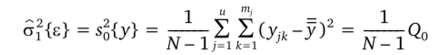
U.

с числом степеней свободы/₀ = N — 1 = Z ггь- 1.

;=i.

2. Несмещенную оценку дисперсии воспроизводимости, вычисляемую как среднюю из и остаточных выборочных дисперсий по и сериям наблюдений.

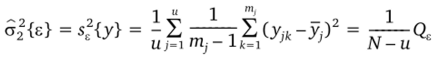
U.

с числом степеней свободы f_x = Nи = T^rrij-u.

3. Несмещенную оценку дисперсии воспроизводимости, вычисляемую по отклонениям и средних у_{, (; = 1, 2, …, и) от общего среднего у:

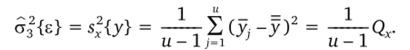
Здесь появляется тп_: потому, что дисперсия единичных измерений в s²_;{y) раз больше дисперсии среднего s²_;{y_;}. Число степеней свободы при этом будет/_А. = и — 1 и должно удовлетворять условию/₀ =/_с +f_x. Действительно: QV- и) + (и — 1) = = N-1.

Из сказанного можно сделать вывод, что если выполняется нуль-гипотеза о незначимое™ влияния фактора х на целевую функциюу, тогда все три оценки дисперсии будут однородными, т. е. будут иметь своим пределом одну и ту же генеральную дисперсию воспроизводимости ст²{е}. Однородность двух дисперсий проверяется по F-критерию Фишера (см. приложение 10):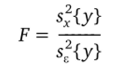

с числами степеней свободы:

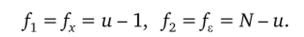
Схема однофакторного ДА при неравном числе т, представлена в табл. 5.12.

Таблица 5.12. Сводка формул

Здесь проверяется нуль-гипотеза Н₀: а²{у} = а²{у}, при альтернативной гипотезе Н^ о²{у} > ст²{у}, поэтому используются таблицы для одностороннего F-критерия. Если влияние фактора х незначимо, то будет выполняться неравенство.

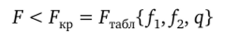
где F — критическое значение F-критерия, взятое из таблиц для уровня значимости q и соответствующих чисел степеней свободы. В противном случае нуль-гипотеза должна быть отброшена как не соответствующая опытным данным, и фактор х признается значимым. Схемы однофакторного ДА представлены в виде табл. 5.13, 5.14, а двухфакторного — табл. 5.15.

Таблица 5.13. Схема однофакторного ДА.

Таблица 5.15. Схема двухфакторного ДА при неравном числе m_ig

Пример 5.10.

Допустим, имеется табл. 5.14 данных измерений тремя приборами (фактор х: j = 1, 2, 3) некоторого показателя качества v, причем выполнено 8 параллельных опытов (к =_ 1, 2, …, 8). По строкам вычисляем у, затем общее среднее у, после чего по строкам получаем суммы квадратов отклонений X (у.-* -у,)²,.

8 8 к=1

Z (у, к -у)². Z (у, -у)², ИЗ них складываются суммы Q₀, Q_x, Q_i:.

fc=l fc=l.

Пример 5.11.

Проверим прибор на качество [25]. Регрессионные модели часто используются для аппроксимации данных, когда истинная функциональная связь неизвестна. Естественно, хотелось бы знать, правильно ли сделано предположение о работе пробной модели. Очевидно, что в этой гипотетической ситуации нужно было использовать полином второго или более высокого порядка; в результате же подобрана очень плохая модель.

Дадим критерий добротности подгонки регрессионной модели. Хотя будет рассматриваться только случай одной независимой переменной, процедура легко обобщается на случай к независимых переменных. Гипотезы, которые хотим проверить:

Н₀ — модель адекватно аппроксимирует данные;

Н_г — модель не аппроксимирует данные.

В процедуру входит разбиение остаточной суммы квадратов на два компонента.

где S_4HCT0IU — сумма квадратов, связанная с «чистой» ошибкой эксперимента; S_Hea;1 — сумма квадратов, объясняемая неадекватностью.

Поскольку в остатке содержится все отличие модели от наблюдения, то в общем случае его можно разбить на случайный и систематический компоненты; последний существует, если модель некорректна. Для вычисления S_4MCT0111 понадобятся повторные наблюденияу по крайней мере при одном уровнех. Предположим, что есть п наблюдений таких, чтоу_п, у₁₂, …, у_1П] — повторные наблюдения при х_х) у_2г, у₂₂, •••" Ущ₂ — повторные наблюдения прих₂;у_т1, у_т2, …, у_т,_т — повторные наблюдения прих,". Видно, что существует т выделенных уровней х. Вклад в сумму квадратов «чистой» ошибки, например, при х_р описывается выражением.

Общая сумма квадратов «чистой» ошибки получается суммированием выражений вида (5.23) по всем уровням х:

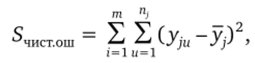
m.

причем с ней связано n_e = 2 (n, — 1) = n — m степеней сво;

i = 1.

боды.

Сумма квадратов, обусловленная неадекватностью,.

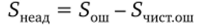
и обладаетп-2-п_е = т-2 степенями свободы.

В основе проверки неадекватности тогда должна лежать статистика.

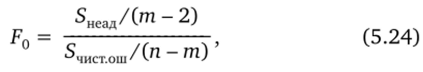
согласно которой Н₀ отклоняется, если F₀ > F_a. _m__2; ,__m.

Процедуру этой проверки можно легко ввести в дисперсионный анализ значимости регрессии. Если нулевая гипотеза об адекватности модели отклоняется, то эту модель нужно отбросить и попытаться найти более подходящую. В противном случае нет очевидных оснований сомневаться в адекватности модели, 5_ЧИСТ0Ш и S_HeaA часто объединяются для получения оценки а².

Пример 5.12

Пусть имеются исходные данные (табл. 5.16).

Таблица 5.16. Данные для примера 5.12.

Можем вычислить S_>y = 10,97, S^ = 13,62, 5^ =52,53 их = = 4,382. Для регрессионной модели получаем у = 1,708 + 0,260х, а для регрессионной суммы квадратов = (3^ = 0,260×13,62 = = 3,541. Процесс нахождения суммы квадратов «чистой» ошибки представлен в табл. 5.17.

Таблица 5.17. Сумма квадратов

Дисперсионный анализ приведен в табл. 5.18. Поскольку Fо,]_{; 8}.₇ = 2,75, то нельзя отклонить гипотезу о том, что подобранная модель адекватно описывает данные. Объединим средние квадраты S_411CT0U1 и S_HCiu для получения среднего квадрата в знаменателе статистики для проверки значимости регрессии. Кроме того, поскольку F_{0 05}. j. ₁₅ = 4,54, то мы должны считать, что р, ^ 0.

Таблица 5.18. Дисперсионный анализ для примера 5.12