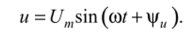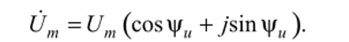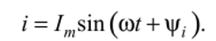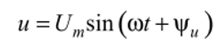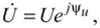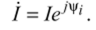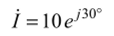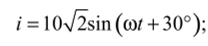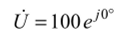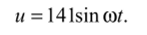Запись синусоидальных токов и напряжений
Какое напряжение изображается этим комплексным числом? Соответствует синусоидальный ток комплексному числу. Запишите комплексное число, изображающее это синусом; Пусть к цепи приложено синусоидальное напряжение. Укажите комплексное число, изображающее этот ток. Соответствует комплексное число. Еще пример. В ветви проходит ток. Действуя по аналогии, находим. Синусоидальное напряжение. Продолжение… Читать ещё >
Запись синусоидальных токов и напряжений (реферат, курсовая, диплом, контрольная)
в символической форме. Переход от символической записи к синусоидальной функции времени Записать ток (напряжение) в символической форме — это значит представить его в виде комплексного числа.
Мы уже научились изображать синусоидальные функции времени векторами, а векторы представлять комплексными числами. Проследив за нашими рассуждениями, нетрудно установить правила непосредственного перехода от синусоидальной функции времени к соответствующему комплексному числу.
Пусть к цепи приложено синусоидальное напряжение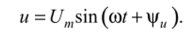 
Запишем это напряжение в символической форме. Построим, как это сделано на рис. 5.5, слева — график (синусоиду) напряжения и справа — его вектор в комплексной плоскости. Полученный вектор представимлсомплексным числом: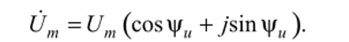 
Рис. 5.5.
Это тригонометрическая форма записи. Применив формулу Эйлера, получим показательную форму:
Еще пример. В ветви проходит ток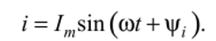 
Требуется записать этот ток в символической форме. Сравнивая между собой написанные выше равенства, замечаем порядок перехода от синусоидальной функции времени к комплексному числу.
Действуя по аналогии, находим.
Выше в символической записи токов и напряжений мы использовали амплитудные значения. Для практических расчетов удобнее пользоваться действующими значениями. Поэтому считают, что функции времени.
соответствует комплексное число.
а функции.
— комплексное число.
Мы научились записывать комплексными числами синусоидальные токи и напряжения. Не вызывает затруднений и обратный переход от символической записи к синусоидальной функции времени. Например, комплексном}' числу.
соответствует синусоидальный ток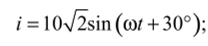 
комплексному числу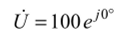 
— синусоидальное напряжение.
В последнем случае начальная фаза равна нулю, а вектор напряжения расположен вдоль положительного направления оси действительных величин.
Карточка № 5.4 (379).
Запись синусоидальных токов и напряжений в символической форме. Переход от символической записи к синусоидальной функции времени.
и = 100 sin (со/-30°). | ит = 1ооИю'" 3°0) | |
Запишите комплексное число, изображающее это синусом; | ит = 100е/3() | |
дальнею напряжение. | Um = 100<�Г, зо°. |
Продолжение карт. № 5.4
и = 100sin (co/ + 135°). Комплексное число, соответствующее этому напряжению, запишите в показательной и алгебрамческой формах. /2. cosl35° = — 5 2. sin 135° = ^~ •. | 0 = !2?е/135‘' = _50 + у'50. л/2. | |
0 = 100ел 35° = -50 V2 + /50 72. | ||
i = 10 cos со/. Укажите комплексное число, изображающее этот ток. | о О. •—V. о|^. II. | |
| ||
/=Ш —у30°. Какой синусоидальный ток изображается этим комплексным числом? | i = -^Lsin (co/-30°). л/2. | |
/ = 10 sin (со/-30°). | ||
i = 10sin (-30°). | ||
7 = ЮО<7|80 Какое напряжение изображается этим комплексным числом? | и = — 100 л/2 sin со/. | |
и = -100sin со/. | ||
и = 100л/2 sin со/ и = 0. |