Множественная линейная регрессия

Рассмотренная нами в предыдущем разделе парная регрессия представляет собой хорошую модель для отработки общих принципов регрессионного анализа. Однако на практике для объяснения вариации признаков в политической науке требуется более одного предиктора. Задачу оценки зависимости одной переменной от нескольких независимых переменных решает множественный регрессионный анализ. Рассмотрим его наиболее простую версию — линейную множественную регрессию методом наименьших квадратов.

Как явствует из сказанного выше, данный вид регрессионного анализа использует тот же метод оценки параметров, что и парная линейная регрессия, — МНК. Соответственно, все сказанное о парной регрессии справедливо и в отношении множественной. Множественная регрессия представляет собой расширение (или обобщение) парной регрессии, а не какой-то принципиально иной метод. Поэтому здесь мы пойдем по пути дополнения тех знаний, которые были получены ранее.

Так, математическая модель множественной регрессии является расширением линейной модели (10.7) за счет включения нескольких предикторов X:

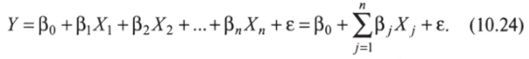
Обратите внимание, что вместе с дополнительными предикторами X мы включаем соответствующие им «угловые» коэффициенты р, (3₂, …, Р". Они «отвечают» за силу и направление влияния предикторов на зависимую переменную. Параметр р₀ и стохастическая компонента е остаются без изменений.

Соответственно, теперь методом наименьших квадратов оценивается уравнение:

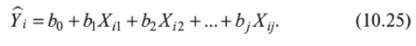
Двойной нижний индекс при X используется потому, что сейчас нам нужно нумеровать не только различные наблюдения (0, но и различные предикторы (индекс J).

По большому счету, существует всего два принципиальных отличия моделей (10.24) и (10.25) от их парных аналогов (10.7) и (10.8). Во-первых, нам придется не только определять степень влияния каждой из независимых переменных на зависимую, но и сравнивать их по этому признаку между собой. Трудности здесь могут возникнуть потому, что разные предикторы могут обладать (и на практике, как правило, обладают) разной размерностью. Во-вторых, несколько независимых переменных могут влиять не только на зависимую переменную, но и друг на друга. Именно этим двум проблемам мы уделим приоритетное внимание в нашем дальнейшем изложении.

Начнем, как обычно, с построения компьютерной модели множественной линейной регрессии.

Упражнение 10.6

• 1. В первом и втором столбцах будут храниться значения переменных XI и Х2. Сгенерируйте по 100 значений в каждом столбце, используя функцию «=СЛЧИС».
• 2. Третий и четвертый столбцы понадобятся нам для того, чтобы получить случайную компоненту. Не забывайте, что она должна обладать нулевым средним. Поэтому в третьем столбце сгенерируем еще одну случайную величину с помощью «=СЛЧИС», а в четвертом вычтем из каждого значения ее среднее арифметическое.
• 3. Следующие три столбца отведем под регрессионные параметры ВО, В1 и В2. Пусть для начала они равны соответственно 0, 1, 1.
• 4. Восьмой столбец предназначен для зависимой переменной Y. Функция для нее должна соответствовать модели (10.25), т. е. Y=B0+B1*X1+B2*X2+E.

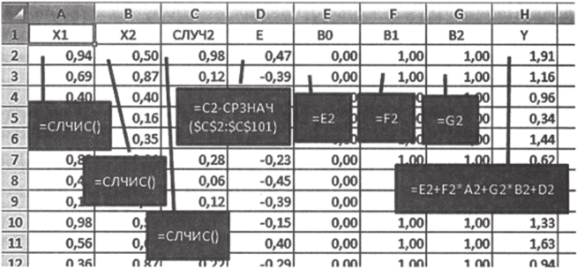
Рис. 10.32

Таким образом, мы начнем рассмотрение множественной регрессии с максимально простой модели У = Х_х + Х₂ + г. Вариации Y, и Х₂ равны по построению, р, = р₂ = 1, следовательно, объяснительная сила каждой из независимых переменных должна быть одинаковой.

5. Постройте диаграммы рассеивания сначала для XI и Y, затем для Х2 и Y. Используйте опции «Добавить линию тренда», «показать уравнение на диаграмме» и «Добавить уровень достоверности аппроксимации R²» (см. рис. Ю. ЗЗя, б).

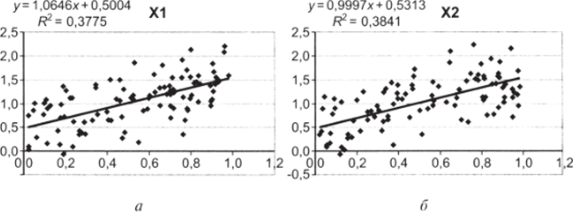
Рис. 10.33.

Оценки />, и Ь₂ разнятся из-за влияния случайной составляющей, однако они колеблются вокруг одной и той же средней (вы можете проверить это на своей модели, нажимая на пустой ячейке клавишу DEL и пересчитывая таким образом случайные величины).

Теперь перейдем к оценке множественной регрессионной модели.

6. Используя надстройку «Анализ данных — регрессия», рассчитайте регрессионную статистику. Не забудьте, что теперь у нас две независимые переменные. Соответственно, входной интервал X должен включать два столбца (именно поэтому мы расположили их рядом при построении модели).

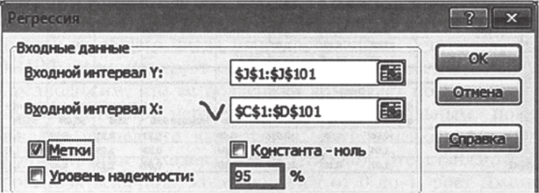
Рис. 10.34.

Принципы интерпретации регрессионной статистики и парной регрессии одни и те же, но есть и некоторые нюансы. Итак, коэффициент детерминации R² показывает, какую долю вариации У объясняют Л^-, и Х₂ вместе. В данном примере «общими усилиями» предикторы объясняют 66% изменчивости У. Стандартная ошибка показывает, что модель с двумя предикторами А', и Х₂ «ошибается в среднем» на 0,3. Результаты дисперсионного анализа интерпретируются точно так же, как и в парной регрессии.

Коэффициент Ь, составляет 1,04. Это означает, что изменение X, на единицу (в единицах измерения Л^-,) приводит к изменению У (в единицах измерения У) в среднем на 1,04 в предположении, что Х₂ при этом не меняется. Коэффициент Ь₂ составляет 1,07; т. е. при изменении Х₂ на единицу (в единицах измерения Х₂) У (в единицах измерения У) меняется в среднем на 1,07 в предположении, что X_t при этом не меняется. Здесь очень важно подчеркнуть: регрессионные коэффициенты показывают влияние соответствующих переменных при фиксированных значениях всех остальных независимых переменных. Сравнивая между собой коэффициенты 6, и Ь₂, мы скажем, что сила их влияния на У примерно одинакова.

Рис. 10.35.

Стандартные ошибки оценок параметров, их статистическая значимость, доверительные интервалы рассматриваются точно так же, как это было нами сделано применительно к задаче парной регрессии.

7. Несколько раз поменяйте параметры В1 и В2 (знак и абсолютное значение), каждый раз рассчитывая регрессионную статистику с помощью пакета анализа.

При изменении параметров BI и В2 в нашей компьютерной модели изменения в регрессионной статистике также будут вполне предсказуемы. Так, сменив знак коэффициента В1 на «-» и рассчитав регрессионную статистику, мы получим соответствующее изменение в знаке оценки />,. Увеличив в два раза параметр В2 (с 1 до 2), вы увидите пропорциональное^[1] увеличение оценки Ь₂. Теперь, сравнив между собой коэффициенты для двух предикторов, вы обнаружите, что Х₂ влияет на У примерно в два раза сильнее, чем X_t.

Однако наша модель устроена таким образом, что Л', и Х₂ являются разными реализациями одной и той же случайной величины: они обладают одинаковым законом распределения, средним, вариацией, размерностью. Кроме того, будучи сгенерированными с помощью случайных чисел, они почти гарантированно не коррелируют между собой. Поэтому нам очень легко их сравнивать. Но в реальном исследовании вы столкнетесь с переменными, которые будут радикально различаться в каждом или почти в каждом из названных отношений. Рассмотрим такой пример, используя реальные данные.

В качестве зависимой переменной возьмем электоральную поддержку партии КПРФ (КПРФ) на федеральных парламентских выборах 2007 г. по регионам России (в процентах от общего числа проголосовавших). Учитывая, что КПРФ позиционирует себя как левая политическая сила, предположим, что ее поддержка возрастает по мере роста имущественного неравенства. Операциональным показателем последнего является, в частности, коэффициент концентрации доходов Джини (Джини). Это стандартизированная величина, колеблющаяся от 0 до 1; рост Джини соответствует росту имущественного расслоения в регионе.

В качестве второй независимой переменной возьмем долю лиц старшего возраста (СВ) в общей численности населения региона (%). Содержательно включение этой переменной основано на том, что значительная часть отстаиваемых КПРФ политических ценностей — социальная справедливость, равенство и т. д. — являлись частью государственной идеологии в СССР. Соответственно, чем старше человек, тем более длительное время он находился под воздействием пропаганды таких ценностей и, соответственно, тем глубже должен был их усвоить. Итак, множественная регрессионная модель выглядит следующим образом:

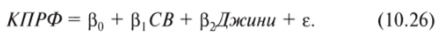
Данные приведены в табл. 10.10 (файл с данными доступен по ссылке http://polit.msu.ru/kaf/lab_quant/).

Упражнение 10.7

1. Сначала составим представление об одномерных распределениях переменных. Постройте гистограммы и рассчитайте основные показатели описательной статистики. Здесь мы приведем средние и стандартные отклонения независимых переменных (см. табл. 10.11).

Очевидно, что в данном случае вариации независимых переменных различаются самым драматическим образом.

2. Рассчитаем парные регрессионные модели и построим соответствующие диаграммы рассеивания. Воспользуемся опциями «Добавить линию тренда», «Показать уравнение на диаграмме» и «Добавить уровень достоверности аппроксимации R²» (см. рис. 10.36а, б).

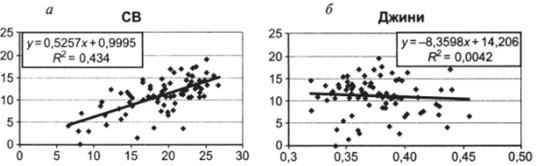
Рис. 10.36.

• 3. Дайте содержательную интерпретацию полученным результатам (к этому пункту мы еще вернемся).
• 4. Используйте «Анализ данных» для оценки множественной регрессионной модели (10.26).

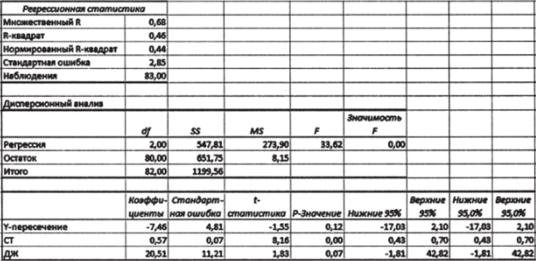
Рис. 10.37

5. Сравните коэффициенты в множественной и парных моделях.

Обратите внимание на один очень важный момент. Коэффициенты b при независимых переменных во множественной модели отличаются от коэффициентов b в парных моделях. Так, если в парной модели рост индекса Джини приводит к снижению поддержки КПРФ, то в множественной модели связь между ними прямая^[2]. Множественная регрессионная модель не является «механической суммой парных связей» между независимыми и зависимой переменными. Оценка влияния предиктора на объясняемую переменную в множественной регрессии зависит от других предикторов, включенных в модель.

6. Сравните между собой коэффициенты при независимых переменных СВ (0,57) и Джини (20,51) во множественной регрессионной модели. Если интерпретировать эти числа буквально, возникает искушение сказать, что влияние имущественного неравенства на поддержку КПРФ примерно в 36 раз сильнее по сравнению с влиянием демографической структуры региона. Однако такой вывод был бы в корне неверным, так как предикторы обладают совершенно разными характеристиками вариации (см. п. 1 данного упражнения) и размерностью: Джини является безразмерным коэффициентом, доля лиц старшего возраста имеет процентную размерность. Коэффициенты b_t, b₂, …, Ь_п в моделях множественной регрессии несопоставимы, их величина жестко «привязана» к размерности соответствующих независимых переменных. Так, коэффициент 0,57 показывает, что увеличение доли людей старшего возраста на 1% (размерность СВ) приводит к увеличению электоральной поддержки КПРФ на 0,57% (размерность КПРФ).

Если нас интересует сравнительная характеристика влияния отдельных предикторов, требуется привести имеющиеся данные к единому масштабу. Практический инструмент решения задачи приведения переменных к сопоставимому виду читателю уже известен — это стандартизация (центрирование и нормировка) данных. Последний раз мы пользовались ей при расчете корреляции Пирсона.

7. Центрируйте и нормируйте переменные КПРФ, СВ, Джини. Эта процедура должна быть уже хорошо знакома читателю, поэтому мы не будем ее комментировать. В случае возникновения затруднений вы можете воспользоваться «шпаргалкой» на рис. 10.38, где нужные функции показаны для переменной КПРФ.

Рис. 10.38.

Теперь все переменные обладают единой размерностью (число стандартных отклонений от среднего), нулевым средним и единичной дисперсией.

8. Рассчитайте статистику множественного регрессионного анализа, используя в качестве зависимой и независимых переменных соответствующие центрированнонормированные величины (столбцы z КПРФ, z СВ и z Джини на рис. 10.38). Результат показан на рис. 10.39.

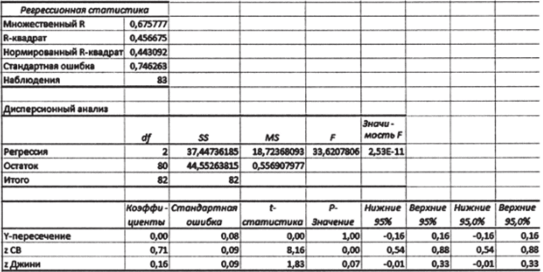
Рис. 10.39.

Теперь в столбце «коэффициенты» вместо параметров А, и Ь₂ мы имеем стандартные коэффициенты регрессии. Иногда их называют «бета-коэффициентами», как в модели (10.24). Однако эта аналогия, вообще говоря, ложная: стандартные коэффициенты регрессии представляют собой оценки параметров, тогда как (5 в модели (10.24) — истинные параметры. Поэтому во избежание путаницы мы будем далее пользоваться только словосочетанием «стандартные коэффициенты регрессии».

Их содержательная интерпретация следующая. Увеличение доли людей старшего возраста на одно стандартное отклонение приводит к увеличению электоральной поддержки КПРФ в среднем на 0,71 стандартного отклонения. Увеличение неравенства в распределении доходов на одно стандартное отклонение приводит к увеличению электоральной поддержки КПРФ в среднем на 0,16 стандартного отклонения. Стандартные коэффициенты регрессии, в отличие от обычных оценок 6, и Ь₂, сопоставимы: мы можем утверждать, что сила влияния демографического фактора на поддержку КПРФ примерно в 4,5 раза больше, чем сила влияния концентрации доходов.

В профессиональных статистических программах, как правило, распечатка результатов содержит сразу оба типа оценок: обычные и стандартные коэффициенты регрессии. Например, так выглядят результаты регрессионного анализа данных в нашем примере, выполненные в SPSS (см. табл. 10.12).

Таблица 10.12

Полужирным шрифтом выделены обычные коэффициенты, заливкой — стандартизированные.

Обратите внимание, что в табл. 10.12 для стандартных коэффициентов отсутствует оценка параметра на рис. 10.39 она имеется и составляет 0,00. Дело в том, что при расчете стандартных коэффициентов регрессии эта оценка всегда будет равна нулю. Это объясняется тем, что линия регрессии всегда проходит через точку (X, У). У центрированнонормированных переменных среднее арифметическое равно нулю по процедуре их расчета. Соответственно, линия регрессии всегда проходит через точку (0,0), никакого смещения по оси ординат нет и, следовательно, нет необходимости его оценивать. Это видно, в частности, на диаграмме совместного распределения z-CB и z-КПРФ (см. рис. 10.40).

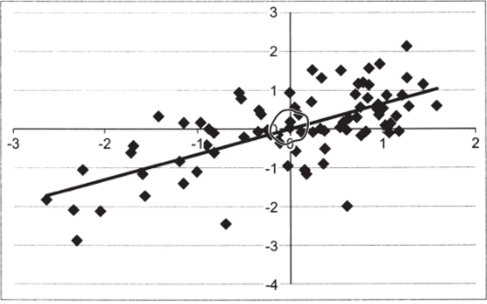
Рис. 10.40.

Еще одна проблема, неактуальная для парной регрессии и имеющая огромное значение для множественной, — проблема мультиколлинеарности. Мультиколлинеарность имеет место, когда существует корреляция между независимыми переменными. К сожалению, в эмпирических исследованиях политики такие корреляции представляют собой скорее правило, нежели исключение. Так, в рассмотренном выше примере с электоральной поддержкой КПРФ корреляция Пирсона между долей лиц старшего возраста и коэффициентом концентрации доходов составляет -0,32. Системы данных с нулевой корреляцией между предикторами встречаются достаточно редко. Поэтому, как правило, есть смысл оценивать не наличие или отсутствие мультиколлинеарности, а степень ее выраженности.

Чтобы понять, почему мультиколлинеарность является проблемой, рассмотрим сначала пример так называемой строгой мультиколлинеарности, когда одна независимая переменная функционально зависит от другой независимой переменной. Содержательно это означает, что две переменные измеряют одно и то же свойство. Например, функционально связаны между собой измерение роста в сантиметрах и измерение роста в дюймах.

Построим модель строгой мультиколлинеарности. Для этого слегка модифицируем компьютерную модель множественной регрессии, построенную нами в упражнении 10.7.

Упражнение 10.8

1. Допустим, переменная Х₂ является линейной функцией переменной X_t. Будем использовать простейшую функциональную связь Х_г = f{X) = X_t. Во втором столбце, где в нашей модели генерируются значения переменной Х₂, замените функцию «=СЛЧИС ()» на функцию «=А…» (см. рис. 10.41). Все остальное оставим без изменений.

Рис. 10.41.

2. Постройте парные диаграммы рассеивания для (Х_ь Y) и (Х₂, К) (рис. 10.42о, б).

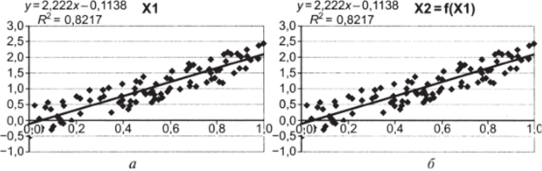
Рис. 10.42.

На диаграммах видно, что влияние каждой из независимых переменных на зависимую переменную совершенно одинаково. Это неудивительно, поскольку один из наших предикторов является «слепком» с другого.

3. Используя надстройку «Анализ данных», рассчитайте статистику множественного регрессионного анализа.

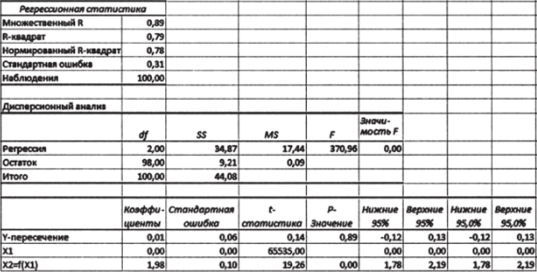
Рис. 10.43.

Ключевые особенности этого результата очевидны. Вся предсказательная сила «перенесена» на переменную Х₂, тогда как коэффициент при Л", обнулен. На самом деле это решение ничуть не хуже любого другого: при строгой мультиколлинеарности вообще не существует «правильного» способа «распределить» между предикторами влияние на зависимую переменную. Кроме того, мультиколлинеарность влияет и на оценки качества модели. В действительности никакие составляющие статистики, которую вы видите на рис. 10.43 (включая R², стандартную ошибку оценки и т. д.), не заслуживают доверия. Точное объяснение этого эффекта потребовало бы использования матричной алгебры, и мы здесь не будем его приводить. Важен практический вывод: наличие статистических зависимостей между предикторами влияет и на сами оценки множественных регрессионных параметров, и на степень нашего доверия к ним.

В политических исследованиях строгую мультиколлинеарность вы, вероятно, никогда не встретите, поэтому будем рассматривать ее как предельный случай. Построим более реалистичную модель взаимовлияния независимых переменных, где корреляция между ними меньше единицы.

Вновь нам потребуется некоторая модификация базовой модели множественной регрессии. Идея моделирования корреляционной связи между Л', и Х₂ состоит в том, чтобы представить Х₂ как линейную комбинацию функциональной зависимости от Х_х и случайной составляющей: Х_г = аХ_х + е.

Упражнение 10.9

• 1. В первом столбце оставим значения XI, генерируемые функцией «=СЛЧИС».
• 2. В третьем столбце поместим параметр а (постоянная), который будет регулировать тесноту связи между Х_х и Х₂. Для начала определим а = 1, что будет соответствовать корреляции примерно на уровне 0,7.
• 3. В четвертом столбце введем еще одну случайную переменную (СЛУЧ1), используя функцию «=СЛЧИС».
• 4. Во втором столбце (чтобы X, и Х₂ были рядом) определим значения переменной Х2=а*Х1+СЛУЧ 1.
• 5. Все остальные части модели, связанные с Y и Е, задаются точно таким же образом, как это было сделано ранее.
• 6. Наконец, в последнем столбце рассчитаем коэффициент корреляции Пирсона для Х_х и Х₂. Он будет меняться с изменением параметра а.

Рис. 10.44

• 7. Рассчитайте центрованно-нормированные значения Х_х, Х₂ и Y, как это было сделано в предыдущем упражнении.
• 8. Зафиксируйте значения случайных величин, используя опцию «Копировать — специальная вставка — значения». Эффект, который мы исследуем, будет отчетливо виден, если переменные не будут пересчитываться.
• 9. Используя «Пакет анализа», оцените полученную регрессионную модель. Обратите внимание, что благодаря центрированию и нормировке в столбце «Коэффициенты» мы получили стандартные коэффициенты регрессии.

В результате получится примерно следующее (см. табл. 10.13, я привел только значение Л-квадрат и стандартные коэффициенты).

Таблица 10.13

Ваш результат, конечно, будет отличаться из-за различий в реализации случайных величин, но принципиально числа должны быть близки к тем, которые вы видите выше.

Теперь изменим направление корреляционной связи между Л', и Х₂:

10. Поменяйте значение параметра ас 1 на -1. Теперь корреляция между независимыми переменными составляет примерно -0,7.

Таблица 10.14

11. Вновь рассчитайте статистику регрессионного анализа (см. табл. 10.14). По идее, мы оцениваем ту же самую регрессионную модель и у нас нет особых оснований ожидать существенных изменений.

Однако изменения имеют место, и весьма радикальные.

Сравните табл. 10.13 и 10.14.

При отрицательной корреляции между независимыми переменными мы наблюдаем почти двукратное снижение объяснительной силы модели, с 0,8 до 0,46. При этом парадоксальным образом оценка влияния отдельных независимых переменных увеличилась.

Поэкспериментировав с параметром а, вы увидите, что его изменение самым серьезным образом влияет на регрессионную статистику до тех пор, пока этот параметр значителен по абсолютной величине (иными словами, пока имеет место сильная корреляция между независимыми переменными). При а = 0,1 и -0,1 эффект изменения знака корреляции будет уже почти несущественным.

Для оценки мультиколлинеарности в моделях множественной регрессии используется тест на толерантность

(«Tolerance»). Оценка толерантности представляет собой величину, принимающую значение от 0 до 1 и обратную мультиколлинеарности. Она рассчитывается для каждой независимой переменной. Чем ближе показатель толерантности к 1, тем слабее корреляционные связи данного предиктора с другими независимыми переменными. Соответственно, нулевая толерантность означает наличие функциональной связи.

При расчете толерантности мы работаем только с независимыми переменными. Идея состоит в том, чтобы рассчитать R² регрессионных моделей, подставляя на место Y каждую из независимых переменных последовательно. Таким образом мы оцениваем совокупное влияние других независимых переменных на данную независимую переменную. Полученные значения R² вычитаются из единицы, чтобы получить величину, обратную мультиколлинеарности.

В нашем примере будут оцениваться модели:

Упражнение 10.10.

• 1. Вернемся к значению а = 1 в предыдущем упражнении. Корреляция между двумя независимыми переменными составляет примерно 0,7.
• 2. Рассчитайте R², используя надстройку «Анализ данных». При этом в качестве зависимой переменной укажите Л', в качестве независимой — Х₂. У меня получилось 0,525, хотя для вашей модели значение будет несколько отличаться.
• 3. Вычтите полученное значение R² из единицы и получите показатель толерантности. В моем примере он равен 1 — 0,525 = 0,475.

В модели с двумя независимыми переменными показатели толерантности для каждой из них будут равны. В моделях с большим числом предикторов каждой независимой переменной будет соответствовать своя оценка.

В профессиональных программах расчет толерантности может осуществляться автоматически. Так, в SPSS есть опция «collinearity diagnostics», включающая данный показатель в общую распечатку результатов (см. рис. 10.45).

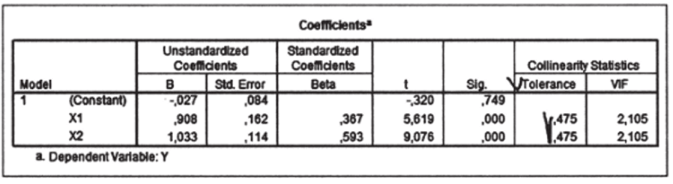
Puc. 10.45.

В заключение этого небольшого введения в множественную регрессию отвлечемся от статистических проблем и вернемся к проблемам сугубо исследовательским. В главе, посвященной корреляции, мы подчеркивали, что наличие корреляции не означает «автоматически» наличия причинно-следственной связи. Этот тезис еще более актуален для регрессионного анализа, который, в отличие от анализа корреляционного, нацелен на поиск причин и следствий. Получение неплохих показателей общего качества модели и значимых коэффициентов при рассматриваемых предикторах еще не дает гарантии того, что включенные в модель факторы в действительности влияют именно таким — фиксируемым регрессионной статистикой — образом на исследуемый признак. Наличие значимых статистических связей может быть эффектом влияния не включенных в модель переменных. Так, регрессия материального ущерба от пожара (зависимая переменная) на число пожарных, участвующих в его тушении (независимая переменная), даст нам очень высокое значение R² и значимый положительный коэффициент />,. Буквальная интерпретация этих результатов такова: чем больше пожарных участвует в тушении пожара, тем больше всякого добра в нем сгорает. «Практическая рекомендация», вытекающая из такого анализа, была бы следующей: надо сократить число пожарных до минимума. Практические последствия внедрения в жизнь такой рекомендации были бы, очевидно, плачевны. А все потому, что мы упустили из виду переменную «интенсивность пожара», которая и является ключевой независимой переменной. Это — характерный пример ошибок спецификации модели.

Чтобы быть уверенным в корректности результатов регрессии, нужно включать в модель не только те предикторы, которые непосредственно интересуют аналитика. Необходимо учитывать все факторы, которые могут оказать влияние на исследуемый признак. Поэтому стандартный дизайн исследовательской регрессионной модели включает два типа независимых переменных: объясняющие и контрольные.

К примеру, нас интересует эффективность региональных систем здравоохранения, и мы рассматриваем влияние уровня финансирования медицины (объясняющая переменная) на продолжительность жизни (зависимая переменная). Но мы не можем ограничиться только этой объясняющей переменной, хотя именно она нас интересует прежде всего. Нужно учесть еще, как минимум, два обстоятельства. Во-первых, на продолжительность жизни влияет не только состояние здравоохранения, но и стандарты образа жизни. В России, например, распространение алкоголизма является значительно более сильным предиктором, чем состояние медицинской сферы. Во-вторых, уровень финансовых затрат на здравоохранение будет зависеть от географии региона, транспортной доступности, особенностей расселения. Так, оказание скорой помощи на Чукотке в среднем значительно дороже, чем в Ивановской области, так как в первом случае иногда приходится использовать авиационный транспорт. Все соображения такого рода должны быть учтены при спецификации регрессионной модели. Наряду с объясняющей в нее следует включить контрольные переменные: например, смертность от алкогольных отравлений и коэффициент транспортной доступности.

Важно помнить, что наряду с «недоспецификацией» модели (отсутствием предикторов, которые должны быть включены) ошибкой является и перенасыщение регрессионного уравнения неработающими факторами. Нельзя включать в модель предикторы «на всякий случай», поскольку каждая независимая переменная влияет на общие результаты анализа и оценки других переменных. Статистическому анализу должен предшествовать очень тщательный содержательный анализ объекта исследования, формулирование четких и обоснованных гипотез о связи между переменными.

• [1] Не строго пропорциональное из-за случайной составляющей.
• [2] Впрочем, не будем забывать о высоком значении стандартной ошибкии, соответственно, довольно низкой точности оценки коэффициента припеременной Джини; кроме того, уровень его значимости не «дотягивает"0,02 до «золотого стандарта».