Предисловие к шестому изданию

Существенным отличием этого издания от предыдущего является включение отдельной главы XI, посвящённой изложению элементов теории эллиптических функций.

И. Привалов.

ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ

В настоящем издании моей книги «Введение в теорию функций комплексного переменного» частично переработан и дополнен текст предыдущего издания. В этой работе принимал участие А. И. Маркушевич, которому я выражаю глубокую благодарность.

И. Привалов.

ВВЕДЕНИЕ

Те операции, которые приходится рассматривать в математике, можно разделить на два класса: прямые и обратные. Так, действию сложения соответствует обратное действие — вычитание, умножению — деление, возведению в целую положительную степень — извлечение корня.

Производя действие сложения над двумя любыми целыми положительными числами, мы в результате этого действия получим всегда число также целое положительное; другими словами, отправляясь от натурального ряда чисел, мы с помощью прямого действия сложения не выходим за пределы этого ряда. Обратное действие — вычитание — выводит нас за пределы совокупности натуральных чисел и становится всегда выполнимым лишь после присоединения к натуральному ряду нуля и целых отрицательных чисел. Следующее обратное действие — деление — требует для своей выполнимости дальнейшего обобщения понятия числа, которое совершается путём введения дробных чисел. Совокупность чисел целых и дробных, называемых рациональными числами, будет замкнутой по отношению к первым четырём основным действиям алгебры: сложению, вычитанию, умножению и делению, т. е. при выполнении любого из этих действий над двумя любыми рациональными числами (кроме деления на нуль) мы в результате получаем элемент той же совокупности — число рациональное. Наконец, обратное действие — извлечение корня — даже в простейшем случае квадратного радикала даёт нам примеры, с одной стороны, чисел действительных, но не рациональных, называемых иррациональными числами, а с другой стороны, чисел вида у V—1,где^{обозначает} действительное число. Числа вида .у V — 1, где у— любое действительное число, не равное нулю, называют чисто мнимыми.

Уже на приведённых примерах видно, что обратные операции приводят нас к необходимости постепенного расширения понятия числа. Если мы перейдём к обратной операции, более сложной, нежели извлечение квадратного корня, — решению квадратного уравнения вида их*-~bx—с = 0, где а, b и с суть действительные числа, то увидим_f что корнями его будут числа вида x—yV—1, где через х и у обозначены числа действительные. Такие числа называются комплексными. В случае у — 0 комплексное ^{, и}сло обращается в действительное, при х = 0, уф О оно будет чис .о мнимым, наконец, в случае у Ф 0 оно называется мнимым числом.-'Совокупность комплексных чисел содержит в себе действительные числа и представляет собою область, замкнутую по отношению ко всем математическим операциям. Так, например, из алгебры известно, что корнями любого уравнения п-й степени с комплексными коэффициентами служат числа комплексные. Возможность производить все математические операции в области комщексных чисел, не выходя за пределы этой области, в значительной. степени определяет собою то огромное значение, какое эти числа имеют в математике.

В настоящей книге мы будем заниматься изучением свойств функций комплексного переменного z = x—yV—1." где х и у суть действительные независимые переменные. Функции комплексного переменного находят себе многочисленные приложения, с одной стороны, в различных прикладных математических дисциплинах, как-то: теоретическая физика, гидродинамика, теория упругости, небесная механика, с другой стороны, в различных отделах чистой математики, как-то: алгебра, аналитическая теория чисел, дифференциальные уравнения и др. Кроме того, теория функций комплексного переменного представляет собою логически стройное и гармонически связное здание, и знакомство с основными вопросами этой теории, бесспорно, является необходимым элементом математического образования.

Чтобы отметить мощность методов функций комплексного переменного, я ограничусь указанием лишь на некоторые крупные достижения, сделанные в области чистой математики с помощью этих методов: труднейшие проблемы распределения простых чисел, как показал ещё Риман, ставятся в зависимость от распределения нулей некоторой функции комплексного переменного; проблема Варннга (Waring) об изображении всякого целого положительного числа в виде суммы ограниченного числа любых степеней, впервые разрешённая Гильбертом, затем была решена английскими математиками Гарди (Hardy) и Литлвудом (Littlewood) на основании методов функций комплексного переменного; труднейшая проблема небесной механики, так называемая задача «о трёх телах», впервые в общем виде была разрешена Зундманом (Sundmann) путём привлечения методов комплексного анализа. Наконец, можно указать многочисленные примеры из основных отделов математики, хорошо знакомых читателю, с целью мотивировать то громадное значение и ту исключительную роль, которые свойственны функциям комплексного переменного.

Ограничимся приведением лишь немногих примеров. Так, предложение о том, что^сякое алгебраическое уравнение имеет по крайней мере один комплексный корень, является основным в алгебре. Далее, из интегрального исчисления хорошо известно о значении, какое имеют компл ексные числа при интегрировании рациональных функций и решении линейных дифференциальных уравнений с постоянными коэффициентами. Необходимо также указать, что многие вопросы классического анализа получили ясное очертание и нашли своё полное решение, лишь благодаря обращению к комплексному анализу. Так, известное тождество Эйлера ef* = cosA'-jWsin х позволило ему ра;

скрыть парадокс Ив. Вернула и Лейбница, заключающийся в следующем.

Замечая, что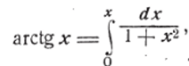

разложим дробь на простейшие дроби ^!):

1 ~р Х"

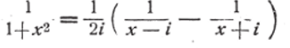
и, проинтегрировав, найдём:

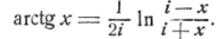
Полагая здесь jc = 1, получим:

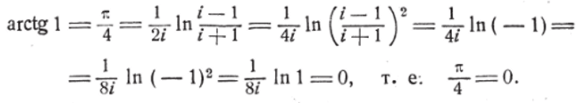
Эйлер раскрыл этот парадокс, показав периодичность показательной функции е*. Действительно, заменяя в тождестве Эйлера х черёз — iz_y получим:

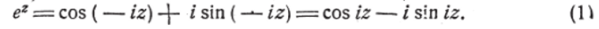
Заменяя в последнем равенстве z через г4−2д/, имеем:

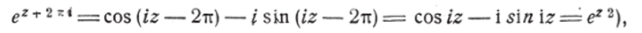
т. е. функция е^[1] не меняет своего значения при замене z на z—2vi, иными словами, 2тт/ есть период этой функции. Определяя натуральный логарифм, z= w из равенства е^[1] =w, мы видим, вследствие периодичности е^[1], что определённому значению w соответствует бесчисленное множество различных значений z— w, разнящихся друг от друга на кратное 2га. Если *гг/^>0, то одно значение z = hw действительное, все остальные мнимые; в случае же w 0 все без исключения значения z = w суть мнимые. Таким образом, логарифмическая функ1шя есть многозначная и парадокс исчезает, если примем In 1 = 2 т.

Тождество Эйлера вскрывает зависимость между функциями тригонометрической и показательной. Далее, из формулы (1) заменой z на —z получаем:

Путём сложения и вычитания тождеств (1) и (2) находим: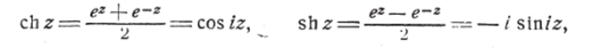

*) В дальнейшем символом / обозначается ^r — 1что даёт выражения гиперболических синуса и косинуса через тригонометрические и, таким образом, позволяет получить все формулы гиперболической тригонометрии, отправляясь от формул обычной тригонометрии.

Укажем ещё на один факт из теории степенных рядов, полное объяснение которого может быть дано лишь с точки зрения функций комплексного переменного. Из анализа известно, что разложение.

имеет место лишь при значениях *, удовлетворяющих неравенству:

| jc <11 — Оставаясь в области действительного переменного jc, мы не в состоянии раскрыть связи между природой функции и фактом сходимости изображающего её ряда лишь при значениях л, удовлетворяющих условию —В самом деле, функция определена для всех значений х в промежутке от —оо до +оо, и значения независимого переменного — 1 и не являются для неё исключительными. Отсюда нельзя понять, почему ряд 1—x²-{-xⁱ — — Л^б +… перестаёт сходиться при значениях х, удовлетворяющих неравенствам: х^—1 и лс^+1. Картина этого явления, однако, вполне выясняется, если рассматривать его в комплексной области.

Действительно, знаменатель дроби ^ _у2 обращается в нуль при.

х = — 1. и, следовательно, эти два значения независимого переменного являются особыми для нашей функции. Изображая комплексное число а. = а—Ы точкой на плоскости с координатами а и b и замечая, что расстояния вышеогмеченных особых точек от начала координат равны единице, мы заключаем: данная функция не имеет особых точек внутри круга с центром в начале координат радиуса единица, в то время как на его окружности имеются особые точки этой функции. Это обстоятельство, как мы далее обнаружим, обусловливает расходимость данного ряда для значений х, модуль которых больше единицы.

В заключение несколько слов о плане настоящего курса. В первых главах мы будем заниматься развитием в комплексной области известных из действительного анализа основных понятий и операций, как-то: предела, производной, интеграла; таким образом, будем строить по аналогии с действительной областью аналитический аппарат для исследования функций комплексного переменного. Построив этот фундамент, мы перейдём к выяснению основных свойств класса дифференцируемых функций комплексного переменного, называемых аналитическими, т. е. изложим наиболее важные отделы теории таких функций.

• [1]) Здесь мы воспользовались периодичностью синуса и косинуса or комплексного переменного. Это будет доказано в гд. II, § 4, п. 7.
• [2]) Здесь мы воспользовались периодичностью синуса и косинуса or комплексного переменного. Это будет доказано в гд. II, § 4, п. 7.
• [3]) Здесь мы воспользовались периодичностью синуса и косинуса or комплексного переменного. Это будет доказано в гд. II, § 4, п. 7.