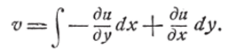Сопряжённые гармонические функции

В дальнейшем мы убедимся в том, что функция, аналитическая в области G, имеет производные всех порядков. В частности, для такой функции и и v имеют непрерывные частные производные второго порядка в области G. Посмотрим, как нужно выбирать и и v для того, чтобы функция и -{- vi была аналитической в рассматриваемой области.

Дифференцируя первое из условий (C.-R.) относительно х, а второе относительно у_у получим:.

складывая эти равенства, имеем:

Уравнение Ди = 0 носит название уравнения Лапласа, и всякая функция, удовлетворяющая этому уравнению, называется гармонической. Итак, и есть гармоническая функция в области G. Покажем также, что и v являете? гармонической функцией в области G. Для этого нужно продифференцировать первое из равенств (C.-R.) относительно у_у второе ж-е относительно х; и вычесть результаты:

Однако, если взять за и и v две произвольные функции, гармонические в области О, то u—vi не будет, вообще говоря, аналитической функцией в этой области. Для того, чтобы и vi была функцией, аналитической в односвязной 'области G, нужно, очевидно, поступить таким образом: взяв за одну из этих функций, например //, произвольную гармоническую функцию, определить затем v из уравнений:

заметим, что выражение.

есть полный дифференциал, так как Да = 0; следовательно, v опрс деляется квадратурами с точностью до придаточного произвольного постоянного: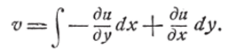

Так определяемая гармоническая функция v называется сопряжённой с гармонической функцией и.