Статистический анализ данных

В том случае, когда визуальный анализ затруднен из-за большого количества данных, следует использовать статистические процедуры. Полученные данные проверяются на одну из статистических гипотез относительно характера распределения вероятностей появления анализируемой совокупности данных. Затем данные, противоречащие этому закону, отбрасываются. Чаще всего предполагают наличие нормального закона распределения. В самом простом случае, когда измеренные величины колеблются около некоторого значения, рассчитываются средняя арифметическая этого значения, дисперсия, доверительные интервалы. Данные, выходящие за эти интервалы, отбрасываются. Естественно, что доверительные границы на этапе предварительного анализа данных должны быть наиболее широкими, с очень высоким уровнем доверительной вероятности.

В случае наличия «выбросов» в исходных данных для получения более точной оценки связи между признаками требуется каким-то образом нивелировать их влияние на оценку модели. Прежде, чем что бы то ни было делать с идентифицированными «выбросами», надо разобраться в том, что они собой представляют и почему произошли. Так, прогнозисту стоит идентифицировать время появления «выброса» и найти экономическое обоснование его существования. В случае если такого обоснования нет, «выброс» можно признать грубой ошибкой. В таком случае с ним можно поступить следующим образом:

• • удалить (если «выброс» пришелся на первые наблюдения в имеющихся данных, сделать это можно безболезненно. Однако если он произошел ближе к концу, то его удаление может повлечь за собой сложности при прогнозировании последних сложившихся тенденций и связей в ряде данных);
• • интерполировать^[1] (в этом случае значение выброса заменяется на некоторое усредненное либо значение соседнего наблюдения. Такая замена решает проблему отсутствия наблюдения, однако интерполяция может лишить прогнозиста важной информации относительно произошедшего наблюдения).

В случае, если прогнозист смог экономически обосновать существование «выброса», он может все так же на свой страх и риск удалить, интерполировать «выброс» либо включить его в модель с помощью фиктивных переменных. В ряде случаев может быть предпочтителен именно третий вариант, так как тогда «выброс» становится частью модели, а не инородным объектом. Подробней о фиктивных переменных речь пойдет в параграфе 4.6.

Источниками систематической ошибки могут являться как инструмент сбора и обработки информации, так и человеческий фактор (желание приукрасить ситуацию или скрыть часть неблагоприятной информации). К сожалению, при работе с вторичными данными социально-экономической динамики (официальной и неофициальной статистикой) часто приходится иметь дело с ошибками, вызванными влиянием человеческого фактора. Особенно это касается данных отечественной статистики и статистики стран — республик бывшего СССР. Дело в том, что большая часть экономических показателей отражает эффективность деятельности того или иного подразделения, той или иной системы, того или иного региона. Классическим примером ошибки информации такого рода являются записываемые год от года в статистические сборники данные о количественных показателях экономического развития бывшего СССР, которые отражали не столько реальные процессы, сколько желаемые результаты. Известно, например, что в Узбекской ССР долгие годы шли приписки о сборе невыращенного хлопка, которые попадали в статистические сборники. По отчетам о выполнении приписанных плановых заданий по сбору хлопка составлялись планы работы текстильной промышленности, которая, соответственно, из несобранного хлопка не могла выпустить несуществующую ткань. Но в статистические отчетности часть этой невыпущенной ткани попадала, а другая списывалась на разного рода потери и брак. Эта цепочка пронизывала весомую часть статистической отчетности, в результате чего ошибочно определялись и производные экономические инструменты — расход хлопка на единицу ткани, нормы электропотрсбления, производительность труда и т. п. Не секрет, что в экономике бывшего СССР осуществлялись и другие приписки. Таким образом, практически все обобщающие данные экономического развития (валовой продукт, национальный доход и т.н.) отдельных регионов, да и страны в целом оказывались год от года засоренными ошибками такого рода.

Сегодня причиной возникновения подобной ошибки может быть, например, желание уменьшить выплаты по платежам в бюджеты и внебюджетные фонды, искажение данных в ходе «информационной войны» с конкурентами и т. п. Многие предприятия в результате этого представляют в статистические органы «засоренную» информацию, и выявить в ней ошибки такого рода практически невозможно.

Есть и другой источник подобной информации. Например, если прогнозист в качестве одного из показателей собирается использовать величину стоимости основных производственных фондов России за некоторый промежуток времени, то он столкнется с рассматриваемой ошибкой. Например, в табл. 2.9 приведены данные по динамике основных фондов и инвестиций по Псковской области^[2]. Из курса «Экономика предприятия» студент знает, что полная стоимость основных производственных фондов в текущем году определяется как остаточная стоимость фондов на конец предыдущего периода плюс инвестиции данного года в основные фонды минус выбытие фондов за год.

Пример

Данные табл. 2.9 свидетельствуют о том, что приведенные значения по основным фондам и инвестициям не вписываются в эту логику. Остаточная стоимость основных фондов, например, в 2006 г. (третий столбец), равная 81 641 млн руб., никак не коррелирует с полной стоимостью основных фондов 2006 г. — 164 095 млн руб. Инвестиции этого года (7603,3 млн руб.) еще больше запутывают суть того, что скрывается за этими цифрами, поскольку если к величине остаточной стоимости прибавить величину инвестиций, то будет получено такое число: 81 641 млн руб. + 7603,3 млн руб. = 89 244,3 млн руб.

Сравнив это полученное с помощью вычислений число с тем, что приводится во втором столбце, можно убедиться, что числа отличаются друг от друга почти в два раза! Объяснить этот двукратный рост с помощью других вычислений невозможно. На самом деле разбалансировка значений объясняется тем, что фактические значения основных фондов, которые собираются на местах, передаются в Росстат (Федеральную службу государственной статистики), где и осуществляется переоценка стоимости фондов по методике, разработанной для этого случая Росстатом.

Таблица 2.9

Некоторые данные по экономике Псковской области.

Окончание табл. 2.9

Эта ситуация с основными фондами, очевидно, характерна для всех областей России и для некоторых республик бывшего СССР, где также производится переоценка основных фондов по собственным методикам. Поэтому прогнозисту в подобных случаях необходимо проводить дополнительные исследования, чтобы понять, как определить ту величину стоимости основных фондов, которую он собирается применить в своих расчетах. Без такой дополнительной работы использовать показатели табл. 2.9 для построения прогнозных моделей нельзя. Понятно, что подобные же перерасчеты, агрегирование и трансформация органами Росстата относятся и к другим показателям социальноэкономического прогнозирования.

Систематические ошибки, вызванные применением неисправного инструмента измерения, могут быть выявлены и исключены, так как имеют примерно одну и ту же величину, один и тот же знак. Поэтому исходные данные, содержащие этот тип ошибки, всегда несколько завышены или занижены. Объективным источником этой ошибки служат, в основном, измерительные устройства, приемы или приборы, вносящие одну и ту же погрешность при измерениях.

Случайные ошибки неизбежны. Причины их появления многообразны и связаны с действием множества случайных неконтролируемых факторов, а поэтому не поддаются анализу. В результате этого практически любое измерение содержит случайные ошибки, но так как источников их возникновения достаточно много, они, как правило, обладают следу ющи м и свойствам и¹.

1. Для ряда результатов наблюдений с известным параметром распределения абсолютные величины случайных ошибок с заданной вероятностью Р не превосходят определенного предела. Это значит, что влияние случайных ошибок на результат все-таки незначительно.

Большаков В.Д. Теория ошибок наблюдений. М.: Недра, 1983.

• 2. Положительные и отрицательные случайные ошибки равновозможны, т. е. одинаково часто встречаются при наблюдениях. Из этого вытекает и следующее свойство.
• 3. Математическое ожидание случайной ошибки равно нулю.
• 4. Малые по абсолютной величине случайные ошибки встречаются при наблюдениях чаще, чем большие.

Следовательно, в большинстве случаев можно предполагать, что случайные ошибки подчиняются закону нормального распределения вероятностей и их математическое ожидание равно нулю. С учетом перечисленных свойств, создается ситуация, когда проявляются условия действия закона больших чисел, в соответствии с которым «совокупное действие большого числа случайных факторов приводит при некоторых, достаточно широких условиях к результату, почти не зависящему от случая»^[3]. Таким образом, избежать влияния случайных ошибок можно, если увеличить объем выборки.

После того, как будут устранены или учтены ошибки информации, перед исследователем встает задача ее систематизации и обработки. В достаточно редких случаях необходимая исследователю информация представлена в систематизированном виде и в виде, пригодном для последующего анализа и обработки. Чаще всего информация представляет собой некоторую неупорядоченную совокупность, нуждающуюся в упорядочении и систематизации.

Систематизация информации заключается в ее представлении в виде таблиц, графиков, диаграмм и в других формах, удобных для исследователя и показывающих некоторые наиболее очевидные закономерности. В большинстве случаев исследователи предпочитают сведение информации в статистические таблицы (при этом возможен их последующий формализованный анализ с помощью математических методов).

Для того чтобы неупорядоченную совокупность данных можно было свести в таблицу, необходимо определить признак упорядочивания данных. Такими признаками могут являться:

• • номер наблюдения;
• • время наблюдения;
• • показатель, по мере увеличения (уменьшения) которого можно упорядочить данные;
• • номера экспертов, дававших оценку объекту исследования;
• • ранги, полученные для свойств товара по шкале отношений или интервалов;
• • товарный ряд и т. п.

Зачастую на практике встречаются случаи, когда сведенная в таблицы информация оказывается неполной — часть данных отсутствует (например, когда при опросе один из респондентов ответил не на все вопросы или в статистическом сборнике не приводятся данные за какой-либо год). В результате возникает необходимость восстановления утерянной в процессе сбора и обработки наблюдений информации. Определить неизвестную величину внутри статистического ряда можно с помощью одного из методов интерполяции.

Теория интерполяции — один из старейших разделов математики, она начиналась работами И. Ньютона, Ж. Лагранжа, Н. Абеля, Ш. Эрмита и др. Интерполирование — это способ нахождения какой-либо величины по известным отдельным значениям этой же или других величин, связанных с ней^[4].

Теория интерполяции является одним из наиболее разработанных разделов численных методов, и поэтому поставленная задача может быть решена с той или иной степенью точности.

Проще всего воспользоваться методом разностей (хотя это и не самый точный метод экстраполяции), суть которого заключается в следующем.

Первая производная функции, как известно, находится по формуле.

Эта производная остается постоянной и не равной нулю, если между двумя переменными существует линейная функциональная зависимость. Если между двумя переменными существует линейная регрессионная зависимость, то в каждой конкретной точке наблюдения за переменными в момент t

первая производная будет иметь значения, в общем случае отличающиеся от значений первой производной в другие моменты времени. Эти отклонения вызваны действием множества случайных факторов и поэтому значения первой производной в разных точках будут колебаться вокруг своего математического ожидания, лучшей оценкой которой в данном случае является средняя арифметическая.

Как вычислить первую производную регрессионной зависимости, если не известны коэффициенты линейной функции, которая описывает эту зависимость? У исследователя имеются в распоряжении только эмпирические значения x_t и y_t. Для решения поставленной задачи первую производную заменяют отношением конечных разностей:

Такая замена возможна только в том случае, когда приращения Ах₍ (конечные разности первого порядка) достаточно малы. Обычно с такой ситуацией и приходится иметь дело на практике. Поэтому легко найти первые разности Ax_t и Ay_t

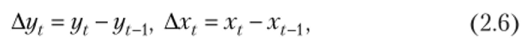
а затем — их отношение: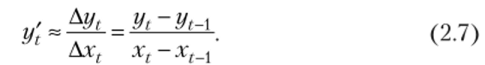

Если это отношение при разных значениях t действительно колеблется около некоторого значения, можно найти одну из оценок этого значения, а именно, среднюю арифметическую:

которая будет в первом приближении характеризовать первую производную зависимости, а значит, будет являться одной из оценок коэффициента линейной регрессии у на х. С помощью этого коэффициента можно решать задачи интерполяции подобных линейных зависимостей. Однако точность такой интерполяции не очень высока, к тому же в практике прогнозирования социально-экономических процессов линейные зависимости встречаются крайне редко. Поэтому метод вычисления конечных разностей для целей интерполяции в настоящее время применяется в простых случаях, но именно конечные разности легли в основу интерполяции методом полинома Ньютона.

Интерполяционная формула Ньютона применяется в том случае, когда упорядоченные значения х₍ находятся на равном расстоянии друг от друга, т. е., когда Ax_t = x_t+1 — x_t = h = = const для всех t. Константа h получила название шага наблюдений (шаг таблицы наблюдений). С учетом этого свойства значения функции двух переменных x_t и y_t характеризуются только изменением переменной y_t. Эти изменения можно определить, вычислив значения конечных разностей. Сами разности можно осуществлять с шагом назад, как это было сделано в (2.6), а можно — и с шагом вперед, как это предусмотрено методом Ньютона. При этом формула для расчета первых разностей будет иметь вид Ay_t = y_t±y_t, вторых разностей — A²y_t = Ay_t+1 -Дг/, третьих — A³y_t = Д²г/,₊₁-д, и так далее для других конечных разностей (табл. 2.10).

Таблица 2.10

Конечные разности различных порядков.

Легко убедиться в том, что если наблюдений будет не шесть, как это показано в таблице 2.10, а, например, восемь, то можно будет вычислить еще и разности шестого и седьмого порядков; если будет Т наблюдений, то можно вычислить разности (Т — 1)-го порядка. Разность каждого порядка некоторым образом характеризует производную степени, соответствующей данному порядку.

Так как значения х₍ в рассматриваемом случае представляют собой арифметическую прогрессию, то, введя обозначение.

получим интерполяционную формулу Ньютона на основе вычисленных значений конечных разностей:

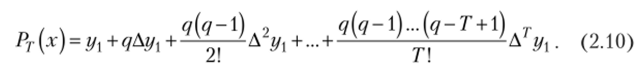
Подставляя в (2.9) известное значение x_t, легко найти q, используя которое в (2.10), вычисляется интерполируемое значение y_t.

Формула (2.10) называется интерполяционной формулой Ньютона для интерполирования вперед^[5]. Существует также формула Ньютона для интерполирования назад, которая использует разности, вычисленные по принципу (2.6).

В случаях, когда необходимо получить более точные результаты интерполяции, рекомендуется использовать и более сложные нелинейные интерполяционные формулы, в первую очередь, интерполяционные формулы Лагранжа. Методика интерполяций этим методом исходит из необходимости построения интерполирующей функции, проходящей через все точки (x_t, y_t). Подобной функцией является многочлен (Г — 1)-й степени, который, очевидно, пройдет через все Т точек:

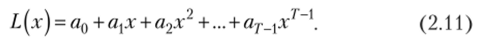
Однако достаточно часто построение подобных функций оказывается излишним, поскольку с подобной задачей могут успешно справиться и функции с более низкими степенями. Именно эту задачу решает метод вычисления интерполяционного многочлена (полинома) Лагранжа, который рассчитывается по формуле^[6]

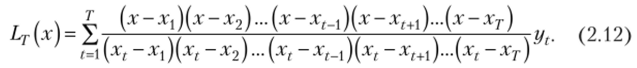
Здесь x_t и y_t — фактические значения наблюдаемых показателей.

Этот интерполяционный многочлен вычисляется для имеющихся пар значений и дает исследователю формулу зависимости интерполируемого значения у (х) = Ь₇{х) от любого значения х. Определив вид этой функции по известному значению x_t (t < Т), интерполируют значение у_р подставляя значение x_t в формулу (2.12).

Каждая из интерполяционных формул (2.8) и (2.10) дает при вычислении ошибки, которые при необходимости можно рассчитать и учесть в вычислениях^[7]. Однако величина этих ошибок достаточно мала, поэтому их влиянием в практике прогнозирования пренебрегают, тем более что эмпирические данные загрязнены другими ошибками, которые мы рассматривали ранее.

К числу методов интерполирования относят также интерполирование методами математической статистики, чаще всего — с помощью МНК. Подробней данный метод будет рассмотрен нами в параграфе 3.5. С учетом того, что сегодня в распоряжении прогнозиста имеются разнообразные пакеты прикладных программ, реализованных применительно к персональным компьютерам, в которых вычисление оценок МНК представляет собой элементарную процедуру, этот способ используют довольно часто.

После того, как информация об объекте прогнозирования собрана, по возможности очищена от ошибок, систематизирована и, при необходимости, восстановлена, прогнозист становится обладателем данных, которые можно использовать для последующих вычислений и построения прогнозных моделей.

• [1] Один из вариантов интерполяции — интерполяция с помощью формулы Ньютона, к которой мы обратимся позже.
• [2] Данные представлены в 2009 г. студентами О. И. Коровкаи Г. К. Бомейко.
• [3] Дунин-Барковский И. В., Смирнов II. В. Теория вероятностей и математическая статистика в технике. М.: Гос. изд-во технико-теоретическойлитературы, 1955. С. 104.
• [4] Янович Л. А. ИH’rcpiюлирование // Математическая энциклопедия. Т. 2.М.: Советская энциклопедия, 1979. С. 622.
• [5] Самарин М. К. Ньютона интерполяционная формула // Математическая энциклопедия. Т. 3. М.: Советская энциклопедия, 1982. С. 1092.
• [6] Кудрявцев Л. ДСамарин М. К. Лагранжа интерполяционная формула // Математическая энциклопедия. Т. 3. М.: Советская энциклопедия, 1982. С. 170−171.
• [7] Хемминг Р. В. Численные методы для научных работников и инженеров. М.: Наука, 1968. С. 110−112.