Частица и одномерный потенциальный барьер

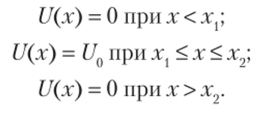
Модели, включающие движение частицы через потенциальный барьер, имеют прямое отношение к описанию скоростей некоторых химических реакций.

Простейшим случаем является использование одномерного прямоугольного барьера. Его потенциальная функция U (x) (рис. 3.2) описывается следующими условиями:

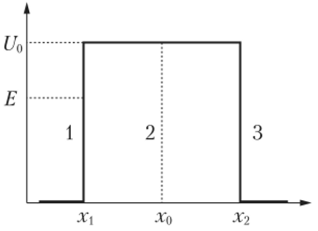
Рис. 3.2. Прямоугольный потенциальный барьер.

В каждой из трех областей такого барьера (на рис. 3.2 они помечены цифрами 1, 2 и 3) волновая функция имеет определенный вид: |/, |/₂ и|/₃.

Для того чтобы волновую функцию считать непрерывной при всех значениях аргумента, необходимо выполнение следующих условий:

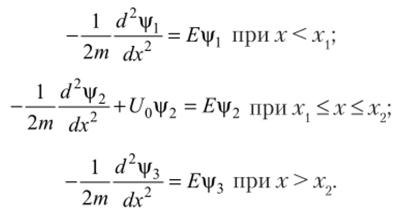
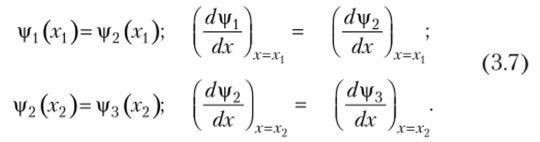
Для нахождения i_{v 2} и |/₃ можно составить три уравнения Шрёдингера, по одному для каждой области:

Введем следующие обозначения:

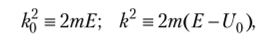
тогда уравнения Шрёдингера запишутся в виде.

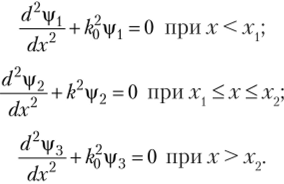
Общий вид решения таких уравнений ранее в изложении материала книги уже встречался, поэтому запишем соответствующие волновые функции в стандартном виде.

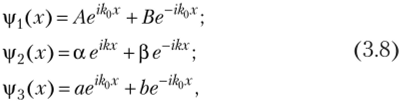
где А, В, а, (3, а, b — постоянные, которые должны удовлетворять условиям (3.7).

Таким образом, волновые функции являются комбинацией двух плоских волн, движущихся в положительном и отрицательном направлениях оси х. Эти плоские волны, из которых состоят функции xj/, v|/₂ и v|/._s, условно имеют следующий смысл:

Ае^{, к}" ^х — волна, падающая на барьер слева направо;

Ве~^{, к}°^х — волна, идущая справа налево в левой части от барьера;

iby ?

ае — волна, идущая слева направо внутри оарьера;

pe"'*^v — волна, идущая справа налево внутри барьера;

ае'^{к, х} — волна, идущая слева направо в правой части от барьера;

Ье‘^к'^{, х} — волна, падающая на барьер справа налево.

Подстановка (3.8) в (3.7) дает.

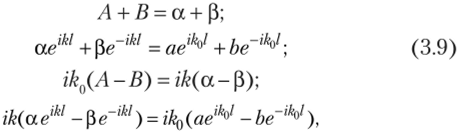
где l=x₂— x.— ширина барьера.

Решая систему четырех уравнений (3.9), можно найти только четыре постоянных из шести: А, В, а, р, а, Ь. Поэтому остальные две нужно определить из других условий задачи.

Для этого ограничим ее предположением, что частица движется к барьеру только слева. Поскольку тогда падающей на барьер справа налево волны нет, то можно положить, что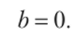

В отсутствие волны be^tk°^x можно уточнить теперь и смысл Be~^lk°^x как отраженной от барьера волны.

Вычислим плотность потока вероятности для падающей волны. По определению (2.8) плотность потока вероятности для одномерной задачи может быть записана в виде.

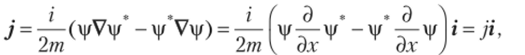
i — орт вдоль оси х.

Тогда для первого слагаемого первой составляющей волновой функции |/, (.г) в уравнении (3.8) — |/_и =Ae^tk°^x, имеем.

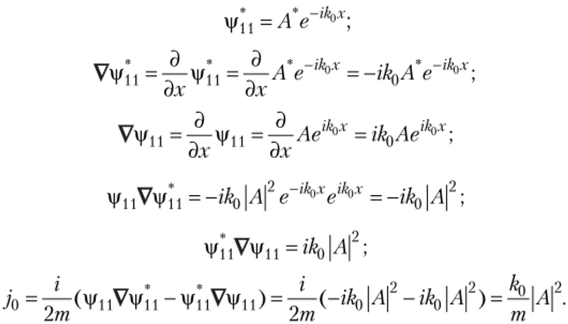
Итак, плотность потока вероятности падающей волны прямо пропорциональна квадрату ее амплитуды. Благодаря такому результату можно еще более ограничить условия задачи, если предположить, что задана такая плотность потока вероятности падающей волны, что ее амплитуда равна единице:

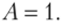
Аналогично можно показать, что плотности потока для отраженной j_r и прошедшей ]₍₁ волны также определяются квадратом их амплитуд:

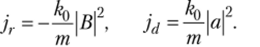
С учетом выбранных значений А — 1 и b = 0 решение системы уравнений (3.9) показывает, что коэффициенты В, а, р и а имеют ненулевые значения. Например, амплитуда прошедшей волны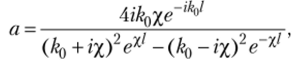

где х ⁼ у]^^т(Ро -?)• Из формулы следует, что даже при энергии частицы, меньшей высоты потенциального барьера (Е < U₀), плотность потока для волны, прошедшей через барьер, отлична от нуля.

Явление прохождения частицы сквозь потенциальный барьер (при Е < U₀) называется туннельным эффектом.

Коэффициентом прохождения D частиц через барьер называется отношение величин плотности потока прошедшей и падающей волны:

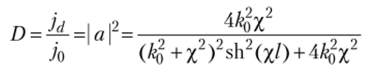
при условии, что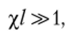

формула для коэффициента прохождения упрощается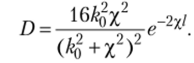

Анализ данных выражений показывает, что коэффициент прохождения D существенно зависит от массы т и разности энергий U_Q — ?, так как квадрат гиперболического синуса резко увеличивается с увеличением аргумента. При некотором значении энергии Е увеличение высоты (U₀) и ширины (d) барьера уменьшает коэффициент прохождения. Для заметного туннельного эффекта должно соблюдаться неравенство.

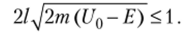
На рис. 3.3 наглядно показано одно из решений, демонстрирующее зависимость плотности вероятности |ц/|~ от координаты х при различном ширине потенциального барьера.

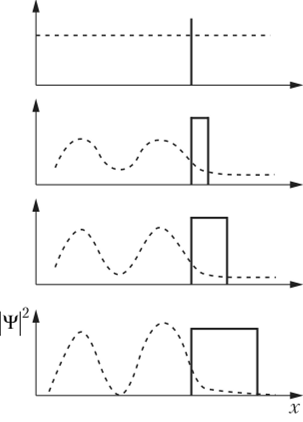
Рис. 33. Зависимость плотности вероятности частицы (штриховые линии) от координаты при различной ширине прямоугольного потенциального барьера (сплошные линии) в случае Е 0

Очевидно, что в отсутствие барьера плотность вероятности всегда постоянна.

Она также всегда постоянна и справа от существующего барьера. Однако она уменьшается при увеличении ширины барьера. Слева от барьера имеет место интерференция между падающей и отраженной волной. Чем шире барьер, тем интенсивнее интерференция волн.

Представления о туннельном эффекте находят экспериментальное подтверждение в опытах по прохождению частицы сквозь потенциальный барьер при а-распаде радиоактивных ядер, холодной эмиссии электронов из металлов в сильных электрических полях, измерениях константы скорости ряда химических реакций (см. подпараграф 18.9.3).

Коэффициентом отражения R частиц от барьера называется отношение величин плотности потока модуля отраженной и падающей волны:

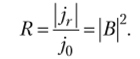
При этом R + D = | В² + а² = 1.

Данный коэффициент отличен от нуля и при энергии частицы выше высоты потенциального барьера.