Уравнение Клейна — Гордона

Воспользовавшись принципом соответствия для энергии (см. параграф 2.5) и опираясь на выражение (7.5), теперь запишем временное уравнение Шрёдингера в виде.

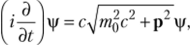
где введен оператор импульса частицы р. Данное уравнение также неинвариантно к преобразованиям Лоренца и содержит в качестве множителя квадратный корень, что придает ему неоднозначность. Эти два недостатка уравнения были преодолены рассмотрением уравнения Клейна — Гордона, полученного возведением в квадрат предыдущего уравнения.

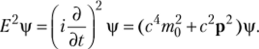
Однако решения данного уравнения не различают положительных и отрицательных значений энергии. Получающаяся плотность вероятности частиц в общем случае не является положительно определенной величиной. Кроме того, оказалось, что уравнение Клейна — Гордона описывает движение частиц со спином, равным нулю, и, таким образом, не годится для электронов, обладающих полуцелым спином.

Уравнение Дирака для свободной частицы

Дирак предложил такую форму релятивистского волнового уравнения, которое имеет не только симметричную форму по отношению к координатам частицы и времени (т.е. инвариантно относительно преобразований Лоренца), но и включает производные не более первого порядка и применимо для электрона.

Для этого Дирак осуществил «линеаризацию» релятивистского соотношения между энергией и импульсом. Линеаризация заключается в «извлечении» квадратного корня с помощью матриц, при этом предполагается, что возможно разложение.

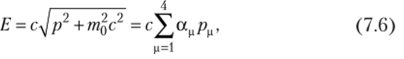
где р. = т₀с, р., = р_х, р._л = р_;/, р_А = р_; а_ц — безразмерные коэффициенты. При этом, очевидно, справедливо следующее равенство:

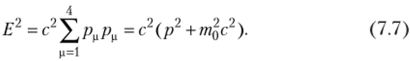
Чтобы найти соотношения между коэффициентами линеаризации а_м, возведем в квадрат уравнение (7.6) и приравняем результат выражению (7.7), тогда получим.

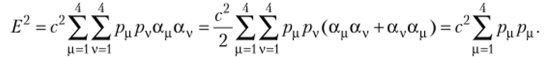
Из последнего выражения следует, что.

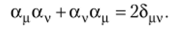
Эго означает, что все четыре величины а_и антикоммутируют друг с другом, т. е.

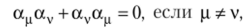
а квадрат каждой из них равен единице.

Полученным условиям удовлетворяют матрицы четвертого порядка.

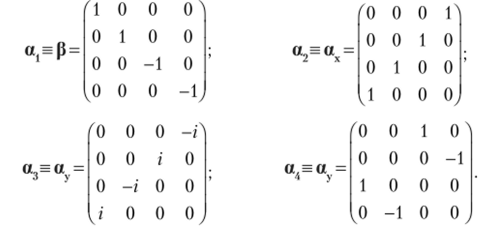
Переходя к операторам, величины следует называть безразмерными операторами, независящими от координат и времени. Так как операторы представляются матрицами четвертого порядка, то и операторы р, р₂, р₃ и р₄ и их собственные функции должны быть представлены четырехкомпонентными векторами. Будем изображать оператор импульса и собственные функции в виде столбцов.

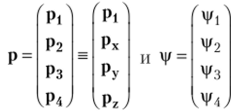
Тогда комплексно-сопряженная функция как собственная функция эрмитового оператора должна быть записана в виде строки.

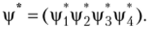
Теперь, как следует из выражения (7.6), гамильтониан Дирака свободной частицы определяется выражением.

Аналогично уравнению Шрёдингера 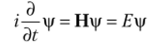теперь запишем уравнение Дирака

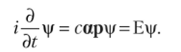
Так же, как и в случае теории Шрёдингера, можно его записать в виде временного уравнения с участием волновой функции в виде матрицы-столбца.

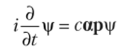
и уравнения для стационарных состояний, включающего энергию как матрицу-строку.

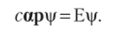
После подстановки конкретных выражений для, а и р и перемножения матриц временное уравнение Дирака в развернутой матричной форме примет вид.

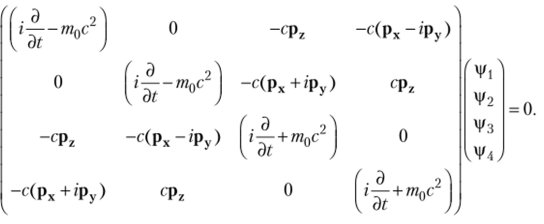
В нерелятивистском пределе квадратная матрица данного уравнения приобретает диагональный вид, так как энергия частицы определяется выражением (7.6) при т = т_п. При этом функции у, и i₂ отвечают положительной энергии (тс²), а функции ц/₃ и |/₄ — отрицательной (-тс²). Первые отвечают электрону, а вторые — позитрону — частице с массой электрона, но с положительным зарядом.

Аналогично матричная форма уравнения Дирака для свободной частицы в стационарном состоянии приобретает вид.

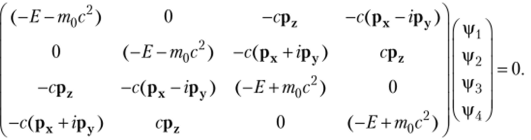
Рассмотрим решение уравнения Дирака для одномерного движения в положительном направлении оси 2 свободной частицы в стационарном состоянии. Для этого примем: р_х = р_у = 0, р₂ = р_г. Теперь матричное уравнение имеет вид.

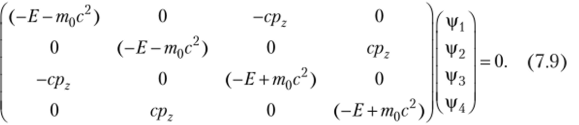
Данное однородное уравнение имеет решение, если его детерминант равен нулю.

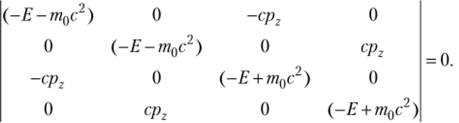
Корни данного уравнения равны 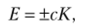где К = ]т?с² + р.

Выберем волновые функции в виде, близком к полученной волновой функции в нерелятивистском приближении (см. параграф 3.1 и формулы (3.1) и (3.2)):

где а — коэффициенты при р = 1, 2, 3, 4; k =р_г =; п = 0, ±1,.

±2,…" ‘ ¹

Для нахождения конкретного вида волновой функции потребуется еще условие нормировки, которое для четырехкомпонентного вектора принимает вид.

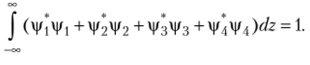
После нормировки экспоненциальной составляющей функции (см. параграф 3.1), подстановки ее в записанное условие нормировки и сокращения постоянного множителя получаем.

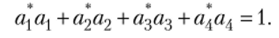
Для определения коэффициентов а^ решим уравнение (7.9) относительно функций. Для этого перемножим матрицы в его левой части: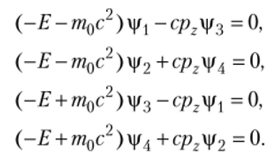

Учитывая (7.10) и обозначая через k_n = т₀с_} получаем.

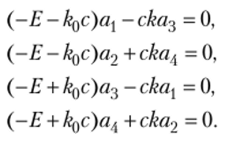
Е.

Вводя подстановку е = — = ±К из полученных уравнений находим ^с

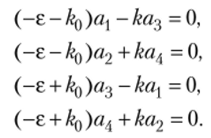
Принимая? = -К, имеем.

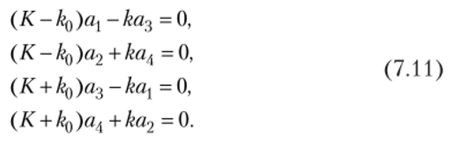
В полученной системе уравнений имеется две пары независимых уравнений. Первая пара — это.

В силу независимости ее от аналогичной системы уравнений с коэффициентами а₂ и а_А для данного решения можно положить.

a., = a_i= 0. Тогда, решая последнюю систему уравнений совместно с условием нормировки af +aj =1, находим первое решение при г= -К

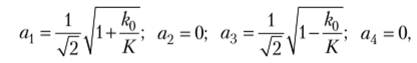
которое запишем в виде вектор-столбца.

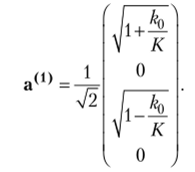
Аналогично, решая вторую систему двух независимых уравнений, из системы (7.11) находим второе решение при в = -К

Поступая подобным образом, находим два решения при г = К

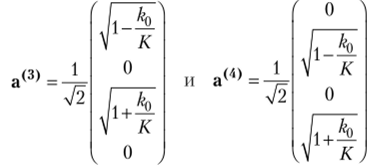
Матричная форма оператора проекции спина на ось z для четырехкомпонентных волновых функций имеет вид (вспомните, что в своем собственном представлении матрица оператора диа;

. 1 V.

гональна, а проекция спина может принимать значения ±—).

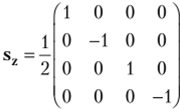
Действуя данным оператором на решение а⁽¹⁾, находим:

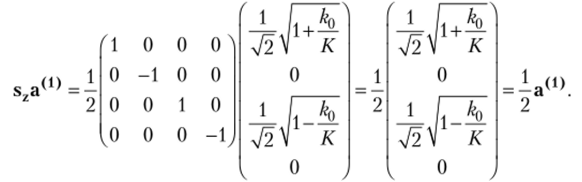
Полученный результат говорит, что собственное значение оператора проекции спина на ось z для решения а^(|) равно Аналогично можно показать, что.

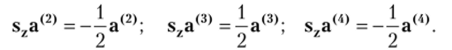
Таким образом, решение а⁽¹⁾ соответствует отрицательной энергии (Е = —К) и направлению спина вдоль оси z. Решение а⁽²⁾, в отличие от первого решения, относится к направлению спина в противоположном направлении оси z. Так же трактуются и решения а⁽³⁾ и а⁽⁴⁾, но при положительной энергии.