Макроскопические характеристики кристаллов

Кристаллы (от греческого krystallos, первоначальное значение — лед) — твердые тела, обладающие трехмерной периодичностью, атомной структурой и при равновесных условиях образования, имеющие естественную форму правильных симметричных многогранников (Б.К.Вайнштейн).

Природные кристаллы, естественные или искусственные, всегда обладают несовершенством строения, вызванным нарушением равновесных условий роста. Однако более важным при рассмотрении реальных кристаллов (кристаллов, встречающихся в природе) является тот факт, что подавляющее большинство реальных кристаллов обладает мозаичной структурой, т. е. реальные кристаллы представляют собой совокупность отдельных кристаллических участков (блоков), имеющих размеры порядка 10'⁴-10'⁵ см, каждый из которых обладает совершенной структурой.

Таким образом, крупный кристалл состоит из большого количества таких блоков, несколько разориентированных друг относительно друга и образующих «мозаику». Величина угла разориентировки может достигать 10−15' (естественные кристаллы каменной соли), но не является строго постоянной для кристаллов даже одного и того же вещества и может меняться в зависимости от условий получения и обработки.

Идеальным кристаллом мы будем называть абстрактный кристалл, обладающий совершенной структурой и всеми характерными закономерностями кристаллического вещества, но не имеющий никаких случайных дефектов.

Строго говоря, законы геометрической кристаллографии применимы только к идеальным кристаллам, но и многие искусственно выраженные в настоящее время реальные кристаллы обладают настолько совершенной структурой, что их можно рассматривать как идеальные.

Одним из наиболее характерных признаков кристаллов является анизотропия — неодинаковость свойств по разным направлениям. Из-за того, что в структуре кристалла в разных направлениях различны расстояния и силы связи между атомами, почти все свойства кристалла различны в разных направлениях (но одинаковы в симметричных направлениях). Анизотропной является и скорость роста кристалла: именно из-за этого кристалл вырастает в форме симметричного правильного многогранника.

Помимо анизотропии, другой специфической чертой кристаллов является их однородность. Точки в кристалле, вообще говоря, различны: в одной точке расположена частица одного сорта (скажем, атом Na в структуре NaCl), в другой — частица иного сорта (атом С1), в третьей атомов вообще нет и т. д. Однако, в целом кристалл однороден — любая его часть ни чем не лучше и не хуже других.

Рис. 3.1. Структура каменной соли.

Однородность кристалла проявляется в существовании так называемого радиуса однородности R: как бы в данном кристалле ни размещать шар радиуса R, в нем наряду с любой точкой содержится одинаково расположенная (гомологичная ей точка), т. е. в шаре однородности содержится по меньшей мере два атома Na, два атома С1 и т. д.

Радиус однородности, как показывают результаты рентгеноструктурных исследований, обычно составляет несколько ангстрем.

В то же время кристалл дискретен — любую точку в кристалле можно окружить шаром дискретности столь малого радиуса, что внутри его не окажется ни одной точки, ей гомологичной. Для разных точек кристалла радиусы дискретности различны, но все они во всяком случае меньше, чем радиус однородности (рис. 3.2).

Здесь с самого начала нужно отметить двойственность подхода к описанию кристаллического вещества: кристаллы можно рассматривать как дискретные (т.е. прерывные) и как сплошные (т.е. непрерывные) среды. Дискретность внутреннего строения означает, естественно, что свойства кристалла не могут быть одинаковыми там, где частица есть, и там, где частицы нет, или в местах, в которых расположены частицы разных сортов. Однако, для описания многих свойств кристаллов достаточно ограничиться рассмотрением объемов, значительно больших, чем собственный объем частицы, и значительно меньших, чем объем кристалла в целом. Именно в таком понимании мы рассматриваем кристалл как среду сплошную и однородную.

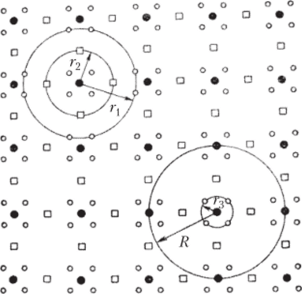
Рис. 3.2. Радиус однородности R кристаллического пространства и радиусы дискретности г, г₂ и г_} отдельных его точек.

Когда кристалл растет, частицы вещества из окружающей среды отлагаются на его гранях, и грани нарастают параллельно самим себе. Меняются площади граней, их форма, отдельные грани могут вытесняться соседними и зарастать, но взаимный наклон граней остается неизменным. Поэтому любое кристаллическое вещество можно однозначно характеризовать взаимным наклоном его граней.

Во всех кристаллах данного вещества при одинаковых условиях углы между соответствующими гранями кристаллов постоянны. В этом заключается закон постоянства углов кристаллов, установленный Николаем Стеноном в 1669 году на основе наблюдений над природными многогранными кристаллами.

Закон постоянства углов объясняется тем, что грани кристаллического многогранника соответствуют атомным плоским сеткам в структуре кристалла, а ребра кристалла — атомным рядам.

Еще одним важным эмпирическим законом геометрической кристаллографии является закон рациональных индексов (закон Гаюи): отношения отрезков, отсекаемых какой-либо гранью кристалла на кристаллографических осях и измеренных в осевых единицах, равны отношениям простых целых чисел. Осевые единицы суть отрезки, отсекаемые на кристаллографических осях единичной гранью. За единичную грань можно взять любую грань кристалла (непараллельную кристаллографическим осям).

Закон рациональных индексов Гаюи имеет большое сходство с законом кратных отношений Дальтона в химии, а также с законами электролиза (электрохимических эквивалентов) Фарадея. Все эти законы целых чисел являются непосредственным проявлением дискретного строения материи.