Получение выражений экономико-математических характеристик для производственных функций фирмы А и фирмы В

Расчет экономико-математических характеристик для фирмы А:

Средние продукты для фирмы А:

Найдем для производственной функции фирмы, А выражения средних продуктов, используя соответствующую функцию.

Средние продукты характеризуют удельный эффект использования ресурсов в производственном процессе фирмы.

1. Средняя фондоотдача — это отношение объема произведенного продукта к стоимости основных фондов:

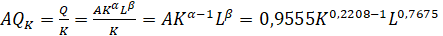
2. Средняя производительность труда — это отношение произведенного продукта к количеству затраченного труда:

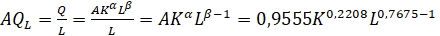
Предельные продукты для фирмы А:

Найдем для производственной функции фирмы, А выражения предельных продуктов, используя соответствующую функцию.

Предельные продукты характеризуют эффект в виде прироста объема продукции, получаемый от увеличения затрат ресурсов.

1. Предельная фондоотдача — характеризует величину дополнительного эффекта от каждой затраченной единицы капитала при данном сочетании ресурсов (K, L):

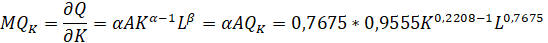
2. Предельная производительность труда — характеризует величину дополнительного эффекта от каждой затраченной единицы труда при данном сочетании ресурсов (К, L):

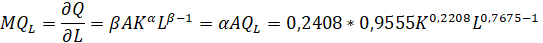
Коэффициенты эластичности по ресурсам для фирмы А:

Коэффициент эластичности показывает процент прироста объема выпуска фирмы при увеличении затрат одного из ресурсов на 1% и неизменном значении другого ресурса.

Эластичность продукта по фондам:

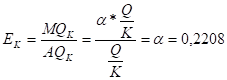
Эластичность продукта по труду:

На основе полученных данных можно сделать вывод, что коэффициенты эластичности для фирмы, А равны соответствующим показателям б и в независимо от затраченных ресурсов, а значит являются стабильными показателями производственной функции.

Предельная норма замещения для фирмы А:

Предельной нормой замены одного ресурса другим называется величина, показывающая, каков объем высвобождаемого ресурса при увеличении затрат ресурса-заменителя на единицу.

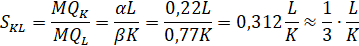
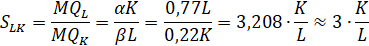
Рисунок 6 — Зависимость предельной нормы замены фирмы, А от первого ресурса.

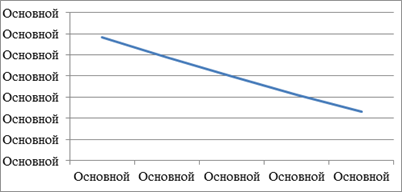
Рисунок 7 — Зависимость предельной нормы замены фирмы, А от второго ресурса Можно сделать вывод, что графики предельной нормы замены представляют собой убывающие кривые, т.к. предельные нормы замены снижаются с увеличением ресурсов-заменителей, как видно на графике. Таким образом, при приобретении дополнительной единицы ресурса К фирма может убрать 3 единицы ресурса L, сохранив неизменный объем выпуска.

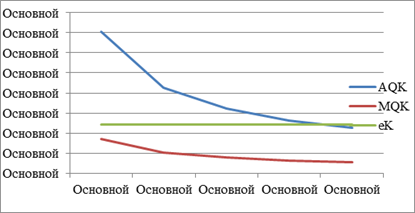
Рисунок 8 — Зависимость среднего, предельного продукта и эластичности первого ресурса фирмы А.

Рисунок 9 — Зависимость среднего, предельного продукта и эластичности второго ресурса фирмы, А Проанализировав рис. 8 можно сделать вывод, что средний и предельный продукты уменьшаются при увеличении затрат первого ресурса, то есть при увеличении капиталовложений с учетом неизменного значения второго ресурса. Средний продукт всегда больше предельного. Таким образом, с увеличением затрат первого ресурса значение предельного и среднего продуктов падает.

Проанализировав рис. 9 можно сделать вывод, что средний и предельный продукты увеличиваются при увеличении затрат второго ресурса, то есть при увеличении трудовых ресурсов с учетом неизменного значения первого ресурса. Средний продукт всегда больше предельного. Таким образом, с увеличением затрат второго ресурса значение предельного и среднего продуктов повышается.

Расчет экономико-математических характеристик для фирмы В:

Средние продукты для фирмы В:

Найдем для производственной функции фирмы В выражения средних продуктов, используя соответствующую функцию.

Средние продукты характеризуют удельный эффект использования ресурсов в производственном процессе фирмы и вычисляются по формулам:

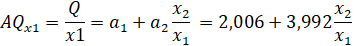
Предельные продукты для фирмы В:

Найдем для производственной функции фирмы B выражения предельных продуктов, используя соответствующую функцию.

Предельные продукты характеризуют эффект в виде прироста объема продукции, получаемый от увеличения затрат ресурсов.

2,006.

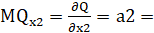
3,992.

Коэффициенты эластичности для фирмы В:

Коэффициент эластичности показывает процент прироста объема выпуска фирмы при увеличении затрат одного из ресурсов на 1% и неизменном значении другого ресурса.

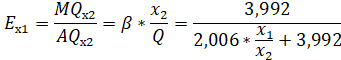
Предельная норма замещения для фирмы В:

Предельной нормой замены одного ресурса другим называется величина, показывающая, каков объем высвобождаемого ресурса при увеличении затрат ресурса-заменителя на единицу.

На основе полученных данных делаем вывод, что предельная норма замены для фирмы В постоянная, не зависит от затраченных ресурсов и равна отношению коэффициентов заменяемого ресурса к заменителю. Это означает, что ресурсы полностью взаимозаменяемы.

Предельная норма замены ресурса х1 на ресурс х2 для фирмы В равна 0,503. Это значит, что при увеличении ресурса х2 на единицу и постоянном объеме выпуска, высвободится 0,503 единиц ресурса х1. Предельная норма замены ресурса х2 на ресурс х1 равна 1,99. Это значит, что при увеличении ресурса х1 на единицу и постоянном объеме выпуска, высвободится 1,99 единиц ресурса х2.

Рисунок 10 — Зависимость средних, предельных продуктов, предельной нормы замены и эластичности первого ресурса фирмы В.

Рисунок 11 — Зависимость средних, предельных продуктов, предельной нормы замены и эластичности второго ресурса фирмы В Проанализировав графики можно сделать вывод, что в фирме В предельный продукт меньше среднего продукта и постоянен, то есть не зависит от изменения затрат первого ресурса. Предельные продукты равны значениям а1 и а2 соответственно. Средний продукт всегда больше предельного продукта и приближается к нему. Таким образом, с увеличением затрат первого и второго ресурса значение среднего продукта уменьшается.

Найдем значения экономико-математических характеристик по данным 4-го и 5-го года.

Для фирмы А:

Таблица 4 — Экономико-математические характеристики для фирмы, А за 4-й и 5-й год.

По сравнению с 4 м годом в 5 году средняя производительность труда увеличилась, а фондоотдача уменьшилась. Средняя фондоотдача в 4-м году равна 0,264. Это означает, что с каждого рубля имеющихся у фирмы, А основных фондов фирма получает прибыль в размере 27 копеек. В 5-м году прибыль равна 23 копейки.

Предельная производительность труда увеличилась, а фондоотдача уменьшилась. Предельная фондоотдача в 4-м году равна 0,064, а в пятом — 0,055. Это значит, что при увеличении ресурса x1 на единицу, выпуск в 4 году вырос на 0,064, а в пятый — на 0,055.

Каждая дополнительно затраченная единица капитала дает все меньший прирост выпуска продукции. Каждая дополнительно затраченная единица труда дает все больший прирост выпуска продукции.

Эластичность ресурсов осталась неизменной, потому как данные показатели зависят от постоянных коэффициентов производственной функции Кобба-Дугласа. Предельная норма замены первого ресурса вторым уменьшилась, как и предельная норма замены второго ресурса первым. Таким образом, в 5 году фирма, А стала работать менее эффективно, т.к. каждая дополнительно затраченная единица капитала давала все меньший прирост объема выпуска продукции.

Для фирмы В:

Таблица 5 — Экономико-математические характеристики для фирмы В за 4-й и 5-й год.

По сравнению с 4 м годом в 5 году средний продукт по первому и второму ресурсам уменьшился. Уменьшение показателей связано с увеличением затрат ресурсов и увеличением объема выпуска.

Предельные продукты остались неизменны, поскольку данные показатели соответствуют постоянным коэффициентам линейной производственной функции. Это означает, что прирост объема выпуска в результате единичного увеличения объема затраченного ресурса х1 или х2 постоянен и не зависит от исходного объема факторов.

Эластичность первого ресурса увеличилась, а эластичность второго ресурса уменьшилась. В 4 год эластичность по ресурсу х1 была 0,438. Это означает, что выпуск продукции увеличится на 43,8% при росте ресурса х1 на 1%. В 5 год эластичность по ресурсу х1 равнялась 0,44, это означает, что при росте ресурса х1 на 1%, выпуск увеличивается на 44%.

Предельные нормы замены первого ресурса вторым и второго первым остались неизменны, потому как данные показатели зависят от постоянных коэффициентов линейной производственной функции. Предельная норма замены ресурса х1 на ресурс х2 для фирмы В равна 0,502. Это значит, что при увеличении ресурса х2 на единицу и постоянном объеме выпуска, высвободится 0,502 единиц ресурса х1. Предельная норма замены ресурса х2 на ресурс х1 равна 1,99. Это значит, что при увеличении ресурса х1 на единицу и постоянном объеме выпуска, высвободится 1,99 единиц ресурса х2.