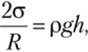Капиллярные явления. 
Коллоидная химия

Лапласово давление в капиллярах, радиус которых соизмерим с кривизной поверхности жидкости, является причиной капиллярных явлений, в частности капиллярного поднятия.

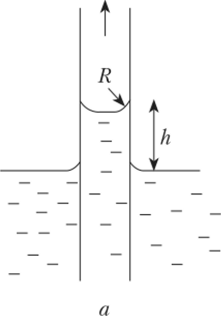
В случае гидрофильной поверхности капилляра на поверхности жидкости образуется вогнутый мениск, лапласово давление направлено к центру кривизны, оно поднимает жидкость (рис. 6.11, а) до тех пор, пока не уравновесится гидростатическим давлением:

где R — радиус мениска, он связан с радиусом капилляра г через косинус угла смачивания: R = rcos0, при cos© = 1 R = г, р — плотность жидкости; h — высота поднятия жидкости в капилляре.

44 0 гидрофильных и гидрофобных поверхностях см. в подпараграфе 6.2.3.

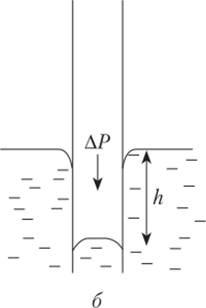
Рис. 6.11. Поднятие жидкости в случае гидрофильной поверхности капилляра (я); опускание жидкости в случае гидрофобной поверхности

капилляра (б)

В случае гидрофобной поверхности образуется выпуклый мениск — жид кость в капилляре будет опускаться (рис. 6.11, б).

Капиллярные явления объясняют многие природные, биологические и технологические процессы: подъем воды в стеблях растений, кровообращение, пропитывание тканей и бумаги красками, формируемость влажного песка и т. п.

Резюме

Капиллярные явления являются следствием капиллярного давления в дисперсных системах.