Основные свойства системы рациональных чисел

Основные свойства полей

По определению система рациональных чисел является полем, поэтому свойства полей являются также свойствами рациональных чисел. Рассмотрим основные свойства поля.

• 4.3.1. Теорема. Пусть дано поле (Р, +, •) с нулем 0 и единицей е. Для любых элементов a, b, c, d еР:
• 1) если я6 = Ь = а~
• 2) (отсутствие делителей нуля) если ab = 0, то а = 0 или b = 0;
• 3) (свойство сократимости для умножения) если ас = Ьс и с Ф 0, то а = Ь;

ас, ,.

4) — =. тогда и только тогда, когда adос; b d

__ч а ^ с ad ± Ьс b d bd

6) — • — = :

b d bd

aa

7) _7 = T;

ь b

" I b

8) если аФ 0, то (-) = -;

b a

. «_. ас a

9) (основное свойство дроби) — = —.

be b

Доказательство. 1) Пусть ab = e. Если предположить, что а = 0, то получим e = ab = 0 b = 0 - пришли к противоречию.

Следовательно, а* 0 и существует элемент а~. Умножив равенство ab = е на а~^х, получим Ь = а~^{.

• 2) Пусть ab = 0. Если а = 0, то доказывать нечего. Если же а* 0, то существует элемент а~^х. Умножив равенство ab = 0 на я^-1, получим b = 0.
• 3) Доказательство свойства сводится к умножению данного равенства на с^-1.
• 4) Пусть — = —, тогда ab~^l =cd~^l. Умножив обе части равенства

b d

на bd, получим ad=bc. Обратное утверждение получаем теми же рассуждениями в обратном порядке.

Доказательство остальных свойств отношений предоставляется читателю. ?

Упорядоченное поле рациональных чисел Введем отношение «меньше» для рациональных чисел с помощью отношения «меньше» для целых чисел. 11ри этом будем считать, что для любого рационального числа — знаменатель b > 0.

b

4.3.2. Определение. Для любых —eQ положим —<�— тогда.

b d b d

и только тогда, когда ad < be.

Легко доказать, что система (Q> <) является линейно упорядоченным множеством. Кроме того, как и для целых чисел, операции сложения и умножения монотонны. Введем общее понятие, частным случаем которого является система (Q, +, •, <).

• 4.3.3. Определение. Упорядоченным полем называется система (Р, +, •, <), удовлетворяющая следующим условиям:
• 1. (Р,+, •) — поле;
• 2. (Р_у<) — линейно упорядоченное множество;
• 3. для любых jc,>", z€P, если х<�у, то x + z (- монотонность сложения), и если х 0, то xz (- монотонноет ь умножения).

Таким образом, система (0, +,•"<) является упорядоченным полем, которое называется упорядоченным полем рациональных чисел.

Рассмотрим произвольное упорядоченное поле (Р, +,?,<) него единицу обозначим через 1. Проведем следующие не вполне строгие рассуждения. Поскольку Р замкнуто относительно сложения, последовательно получаем: 2 = 1 + 1 еР, 3 = 2 + 1 еР, … Поскольку 1>0, то 2>0, 3>0, … Таким образом, мы получаем, что все новые и новые натуральные числа принадлежат Р. В итоге убеждаемся, что Nc/ Но поле вместе с каждым своим элементом содержит ему противоположный, следовательно, -N^P. Итак,.

Z = Nkj{0}^j-NС.Р. Но в поле из того, что w. weZcP и /?*0,.

следует, что т, п~^] еР, откуда — = /и-л^-1 еР. Таким образом,.

п

Q = Д т, п е Zyti * 0 (сР, то есть всякое упорядоченное поле п

содержит упорядоченное поле рациональных чисел (образно говоря, ухватившись за единицу, мы втянули в Р все множество Q). Докажем это утверждение в более строгом виде.

4.3.4. Теорема. Всякое упорядоченное поле содержит упорядоченное подполе, изоморфное упорядоченному полю

рациональных чисел.

Доказательство. Пусть дано упорядоченное поле (Р, +, ?, <).

те

с единицей е. Обозначим Q = {— | т, п eZ, n*Q} и определим.

пе

отображение —>??, положив (р{—) = — для любого —eQ.

п пе п

Докажем, что <�р является изоморфизмом (??,+,-, на (Q, +,-,.

1. (р — взаимно однозначное отображение. Пусть (р{—) = (р(—),.

п /?|.

т w.., ш_ч лп. те т, е

докажем что — = —-. Из условия (р{—) = (р{—-) получаем — = —=-, п щ п л, пе ще

откуда те• ще = т_хе• пе и тп_хе = т_хпе. Предположим, что тп_хФт_хп> пусть, например, тщ <�пцп. Тогда т_хп-тп_х >0, то есть т_хп-тп_х е N и (т_]п-тп₁)е = 0. Но в 3.3.15 доказано, что в упорядоченном кольце, а значит и в упорядоченном поле, для любого натурального числа к имеем ке> 0 — пришли к противоречию. Следовательно, тп_х = т_хп, т пи

откуда — = —-. п п_х

• 2. Очевидно, (р — отображение на Q.
• 3. Докажем, что (р сохраняет операции сложения и умножения, а

также отношение «меньше». Для любых —€ Q имеем:

л л,.

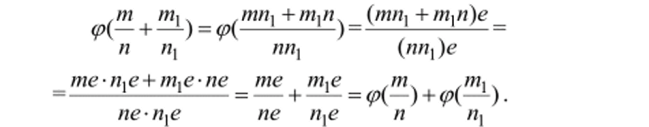
Для умножения — аналогично. Наконец, (р сохраняет отношение т пц _ _.

«меньше», так как — 0, л, > 0, тогда и только тогда, л л, когда /л л, </л, л. Но это равносильно /л, — л-/л-л, e;V, и по 3.3.15,.

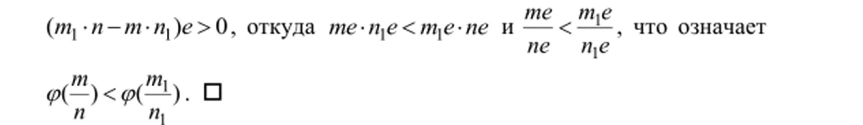
Нетрудно видеть, что изоморфный образ упорядоченного поля рациональных чисел есть упорядоченное поле рациональных чисел, поэтому из доказанной теоремы получаем следующую краткую характеризацию этой числовой системы.

4.3.5. Следствие. Система (Р, +,-,<) есть упорядоченное поле рациональных чисел тогда и только тогда, когда она является минимальным упорядоченным полем.

Если между целыми числами л и л +1 нет ни одного целого числа, то между любыми двумя различными рациональными числами можно найти новое рациональное число. Отметим это свойство в наиболее общем виде.

4.3.6. Предложение. Во всяком упорядоченном поле (Р, +,-,<) для любых элементов a, bеР, где а<�Ь, существует элемент cgP такой, что а<�с<�Ь.

Доказательство. Можно взять, например, с = ^а+ е Р.

4.3.7. Теорема. Упорядоченное поле рациональных чисел удовлетворяет аксиоме Архимеда: для любого положительного aeQ и любого Ь&0 существует натуральное число п такое, что па>Ь.

Доказательство. Пусть а = —, где kjneN, и Ь = — _у где.

k q

psZ, qsN. По аксиоме Архимеда для целых чисел, для целого числа mq > 0 и целого числа кр существует натуральное число п такое, что nmq>kp. Пользуясь монотонностью умножения, разделим это неравенство на kq> 0. Получим п— > —, то есть па>Ь. ?

к q