Критерии согласия. 
Теория вероятностей и математическая статистика

В результате освоения материала данной главы студент должен: знать

• • критерий согласия Пирсона и критерий согласия Колмогорова;
• • критерий однородности; уметь
• • строить гипотезу о предполагаемом законе распределения и проводить ее проверку;

владеть

• навыками построения и проверки гипотез.

Критерии проверки гипотезы о предполагаемом виде закона распределения случайной величины называются критериями согласия. Термин «согласие» применен для обозначения того обстоятельства, что проверяется не принадлежность выборки предполагаемому распределению, а только факт отсутствия противоречия с рассматриваемым законом распределения, согласие с ним. Критические статистики этих критериев основаны на разных мерах расстояний между анализируемой эмпирической функцией распределения и предполагаемой.

Гипотеза называется простой, если проверяется согласие с законом распределения с известными параметрами F (x, 9), где 0 — параметр распределения или вектор параметров.

Гипотеза называется сложной, если проверяется соответствие не определенному закону распределения, а модели закона распределения, определяемой целым параметрическим семейством с неизвестными параметрами. Например, закон распределения анализируемой случайной величины описывается нормальной моделью. В этом случае параметры оцениваются по выборке.

Критерий согласия Пирсона

Критерий согласия Пирсона основан на теореме Пирсона и позволяет проверить соответствие выборки закону распределения как для дискретных, так и для непрерывных случайных величин.

Теорема 16.1 (Пирсона). Пусть имеется п независимых испытаний, каждое из которых может:

• • в дискретном случае иметь г различных исходов (ячеек) А_ь А₂,…, А_г с числом значений в каждом соответственно т_ь т₂, …, т_г и соответствующими вероятностями р_ь р₂, …, р_г, причем Ур, =1;
• • в непрерывном случае попасть в один из г различных промежутков (-оо; cj, (с_х; с₂], (с_г_!; +°°], на которые разбита область значе

ний случайной величины, с числом значений в каждом соответственно т_ь т₂, …, т_ги соответствующими вероятностями р_ь р₂, …, р_г попадания в эти промежутки, причем Ур, — =1;

и пусть проверяется простая гипотеза на согласие с законом распределения с известными параметрами F (x, 0). Тогда если гипотеза истинна,

/ 2.

I щ

г [ll~^pi

то распределение статистики пУ—— при п —> оо сходится крас-

i=i Pi

пределению хи-квадрат с г — 1 степенями свободы. Если гипотеза неверна, статистика стремится к бесконечности.

Замечание 16.1. Уровень значимости теоремы не сравним с ЦПТ или теоремой ММП, а сложность доказательства сопоставима. Поэтому ограничимся обоснованием.

1. Разбиение независимых испытаний на г различных исходов позволяет рассматривать исходы как испытания Бернулли, где успехом является попадание в ячейку A_i в дискретном случае или в промежуток (с_;__х; с_г] в непрерывном. Тогда т_; — число успехов, т. е. число попаданий в i-ю ячейку или /-Й промежуток в п испытаниях Бернулли. Величина —.

п

есть относительная частота успехов, которая является несмещенной, состоятельной, асимптотически нормальной оценкой вероятности.

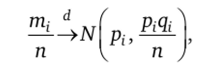
откуда.

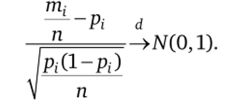
f m, f.

r V'^Pi

2. Определим число независимых слагаемых в сумме п?--—.

i=l Pi

Вначале рассмотрим случай г = 2, т. е. т_г + т₂ = п. Тогда.

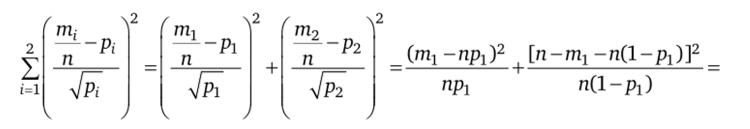
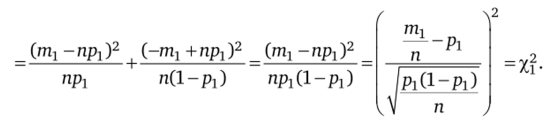
Таким образом, в сумме, содержащей два слагаемых, число степеней свободы равно единице. Это связано с наличием уравнения т₁ + т₂ = п.

3. В общем случае число независимых переменных останется на единицу меньше числа г, поскольку сохраняется связывающее их уравне;

т,.

Pi

ние. Действительно, если статистика имеет вид .— уп и.

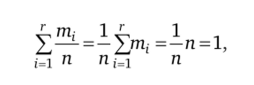
то можно подобрать такие весовые коэффициенты од перед q,-, не все равные нулю, что =0. Например, а, — = л/р7^:

i=i.

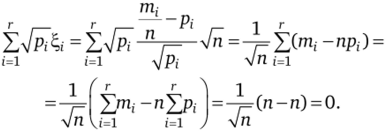
4. При п —> оо вероятность р, мала, величина q, —> 1. Поэтому.

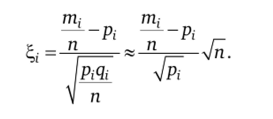
Составим из асимптотически распределенных по стандартному нормальному закону случайных величин сумму квадратов. Она будет распределена по закону хи-квадрат с г — 1 степенями свободы:

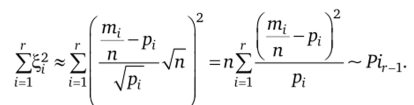
_r -a)²

Таким образам, распределение статистики nY--— при п —" оо.

i=i Pi

сходится к распределению хи-квадрат с г — 1 степенями свободы.

5. Если основная гипотеза неверна, то найдется такой номер к е

е {1, 2, …, г}, что Тогда при любом сколь угодно большом зна;

п

^тк IT.

чении п разность ——~Рк =ос_п ^не сходится по вероятности к нулю. Поэ- п

тому при п —> со.

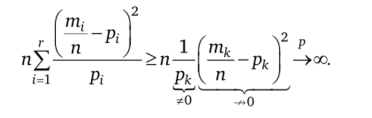
Строгое доказательство теоремы для произвольного п содержится в учебной литературе¹.

Замечание 16.2. Число степеней свободы распределения хи-квадрат будет меньше числа независимых случайных величин при наличии уравнений связи или при использовании статистик, являющихся комбинациями независимых случайных величин. Например, если проверяется выборка на согласие с нормальным распределением, математическое ожидание и дисперсия которого неизвестны, приходится искать их по выборке, связывая двумя уравнениями случайные наблюдения. Число степеней свободы в этой задаче равно г — 5 — 1, где s — число определяемых по выборке параметров гипотетической функции распределения.

Алгоритм проверки гипотезы в непрерывном случае следующий.

• 1. Из генеральной совокупности производится выборка объема п.
• 2. Составляется сгруппированный статистический ряд.
• 3. Весь диапазон наблюдаемых значений разбивается на г частичных интервалов
• (-оо; с_х], (с_х; с₂],…, (с_г__х; +<�"].
• 4. На основании гипотетической функции распределения F (x, 0) вычисляются вероятности попадания случайной величины? в частичные интервалы

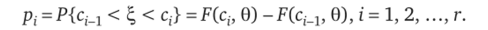
_Р (^-аТ.

5. Вычисляется статистика хи-квадрат: yj =пУ——.

_ ы Pi

¹ См., например: Боровков А. А. Математическая статистика. СПб.: Лань, 2010.

• 6. По заданному уровню значимости, а и числу степеней свободы г — - 1 находится критическая точка х_кр = х_а. _г__х.
• 7. Если Xn > ^a;r-i> ^то гипотеза Н₀ отклоняется, гипотеза Н_} принимается; гипотетическая функция распределения не согласуется с опытными данными. Если Хп ^<�ха-, г-ь ^т0 гипотеза Н₀ принимается; предполагаемая функция F{x, 0) согласуется с опытными данными.

Замечание 16.3. Выбор конкретного числа интервалов должен осуществляться из следующих соображений. При оптимальном группировании вероятности попадания в интервалы в общем случае не равны. Обычно минимальны вероятности попадания в крайние интервалы. Поэтому число интервалов желательно выбирать из условия пр, > 5 для любого интервала при оптимальном группировании. По крайней мере минимальная ожидаемая частота должна быть больше единицы. Опыт статистического оценивания показывает, что для количественной оценки требуется число наблюдений не менее 50. Число интервалов желательно иметь не менее 6—10, причем в каждый интервал должно попасть не менее 5—7 наблюдений. Интервалы с меньшим числом наблюдений следует объединять.

Пример 16.1. Редактором издательства собраны и представлены в таблице статистические данные о числе ошибок, совершаемых авторами статей в расчете на авторский лист текста.

В таблице i — число ошибок в одном из т, авторских листов. Используя критерий Пирсона, проверить на уровне значимости 0,01, что число ошибок в тексте распределено по закону Пуассона с параметром Х = 4.

Решение. Рассчитываем теоретические вероятности в распределении Пуассона Р (% = 0 = г~е~⁴.

Составляем и рассчитываем сумму:

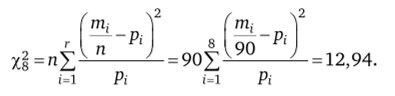
По таблице хи-квадрат для, а = 0,01 находим х_а;г_₁=х_001;7= 18,5. Поскольку Хп можно согласиться на распределение Пуассона с параметром X = 4.