Матрица скидок. 
Управление запасами в цепях поставок

Для различных вариантов моделей расчета оптимальных партий заказа, основанного на уравнении общих логистических затрат, сформирована матрица возможных (их более 70) комбинаций пяти видов скидок. Представленные в табл. 5.23 варианты дополняют известные модели I и II (см. табл. 5.21) и вместе с ними охватывают весь спектр наиболее популярных вариантов учета скидок, учитываемых в управлении запасами.

В табл. 5.18 учтены пять видов скидок: C_n(<2i) — скидки при закупке с единицы продукции; C₀(Q₂) — скидки на организацию заказа; a (Q₃)k — скидки на хранение большой партии при аренде склада; C_T(Qi) ~ изменение тарифа на перевозку партии заказа; C_T(Q5) — изменение тарифа на перевозку единицы продукции.

Таблица 5.18

Формирование составляющих затрат в моделях EOQ в условиях применения скидок¹

Примечание. С₀ — затраты на организацию заказа; а — затраты на содержание единицы запаса с учетом занимаемой площади (объема) склада, руб/м² или руб/м³; k — коэффициент, учитывающий пространственные габариты единицы запаса, м²/ед. или м³/ед.

* Затраты на хранение в зависимости от цены единицы продукции.

** Затраты на хранение в зависимости от размера занимаемой площади склада.

Запись в табл. 5.18 означает, что, например, модель II 1а включает три вида скидок: C_n(Qi), C_q(Q₂) и ak (Q₃). Также из табл. 5.18 видно, что наиболее сложные модели включают четыре вида скидок.

Наиболее простой моделью является модель 1а, учитывающая скидку на закупку с единицы продукции, где затраты на организацию заказа и затраты на хранение не зависят от размера заказа (Qj).

Уравнение суммарных затрат имеет вид:

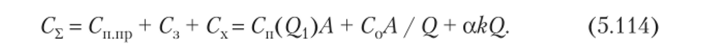
Аналитическая зависимость C"(Q) записывается в виде дискретной формулы (5.112). Затраты на закупку продукции с увеличением размера^[1]

заказа уменьшаются дискретно, затраты на организацию заказов уменьшаются, подчиняясь гиперболической зависимости, затраты на хранение заказа возрастают прямо пропорционально размеру заказа, кривые общих затрат имеют вогнутый характер, что говорит о наличии минимума, соответствующего оптимальной партии заказа (Q), в каждом интервале цен при оптовых закупках. Графически модель 1а представлена на рис. 5.8, из которого видно, что в варианте 1 оптимальная партия заказа находится в интервале Q₂ < Q < Q_n> а в варианте 2 в интервале Q_{ < Q < Q₂.

Рис. 5.8. Графическое представление модели 1а:

вариант 1 — оптимальная партия в интервале Q₂ < Q< Q,; вариант 2 — оптимальная партия в интервале Qj < Q < Q₂

Модель 1б учитывает скидку на закупку и хранение с единицы продукции.

Уравнение суммарных затрат, в котором в двух составляющих затрат С_{п п}р и С_х учтены скидки, имеет вид:

Графически эта модель представлена на рис. 5.9, из которого видно, что затраты на закупку продукции с увеличением размера заказа уменьшаются дискретно, затраты на организацию заказов уменьшаются, подчиняясь гиперболической зависимости, затраты на хранение заказа возрастают прямо пропорционально размеру заказа в каждом интервале, кривые общих затрат имеют вогнутый характер, что говорит о наличии минимума, соответствующего оптимальной партии заказа (ОД в каждом интервале цен при оптовых закупках, оптимальная партия заказа определяется интервалом размера заказа. В варианте 1 оптимальная партия заказа находится в интервале Q₂< Q< Q_n> в варианте 2 — в интервале Q_{< Q< Q₂

Модель Шб учитывает скидку на закупку, хранение с единицы продукции и организацию заказа. Уравнение суммарных затрат, в котором в трех составляющих затрат С_{п пр}, С._Л и С_х присутствуют скидки, имеет вид:

Аналитические зависимости C"(Qi) и C₍₎(Q₂) записываются в виде дискретных формул:

Рис. 5.9. Графическое представление модели 1б: а — составляющие затрат модели 16; б — варианты общих затрат модели 1б:

вариант 1 — оптимальная партия в интервале Q₂< Q< Q,; вариант 2 — оптимальная партия в интервале Q, < Q < Q₂

и На разные затраты поставщики могут предоставлять скидки в разных интервалах размера поставки. Так, в данном примере интервалы размера поставки (Qj), в которых предоставляются скидки на оптовую закупку и на хранение, совпадают, а скидка на организацию заказа предоставляется в ином интервале размера поставки (<2₂);

Графически эта модель представлена на рис. 5.10. В случае если интервалы предоставления скидок на все три составляющие будут совпадать, модель будет иметь графическое представление, соответствующее рис. 5.11.

Из рис. 5.10 и 5.11 видно, что затраты на хранение заказа возрастают прямо пропорционально размеру заказа в каждом интервале, а затраты на приобретение продукции и на организацию заказов с увеличением размера заказа уменьшаются.

Рис. 5.10. Модель Шб с применением скидок в различных интервалах.

размера поставки.

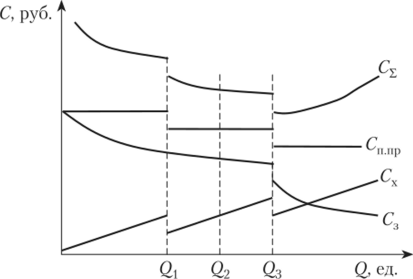
Рис. 5.11. Модель Шб с применением скидок в одинаковых интервалах.

размера поставки.

Модель VII учитывает скидку на закупку и организацию заказа.

Уравнение с двумя переменными, С_п пр и С._Л, имеет вид:

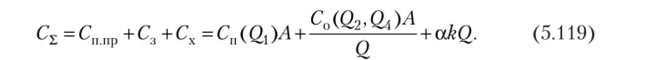
Графически эта модель представлена на рис. 5.12, из которого видно, что затраты на приобретение продукции и на организацию заказов с увеличением размера заказа уменьшаются, а затраты на хранение заказа возрастают прямо пропорционально размеру заказа. Оба варианта рассматривают применение оптовой скидки и скидки на организацию заказа в различных интервалах размера поставки.

Модель Шв учитывает скидку на закупку заказа, хранение с единицы продукции и большой партии заказа при аренде склада.

Рис. 5.12. Графическое представление модели VII:

вариант 1 — скидки на закупку и скидки на организацию заказа предоставляются в частично совпадающих интервалах размеров поставки; вариант 2 — скидки на закупку и скидки на организацию заказа предоставляются в полностью несовпадающих интервалах размеров поставки Уравнение имеет следующий вид:

Модель X учитывает скидку на закупку и организацию заказа, хранение с единицы продукции и большой партии заказа при аренде склада. Уравнение имеет следующий вид:

где Д — коэффициент, отражающий соотношение затрат на хранение, 0 < < Д < 1.

Общая модель суммарных затрат на управление запасами учитывает скидку на закупку и организацию заказа, хранение с единицы продукции, хранение большой партии заказа и страхового запаса при аренде склада (модель IX).

Уравнение имеет следующий вид:

• [1] Проблемы формирования прикладной теории логистики и управления цепями поставок / под общ. ред. В. С. Лукинского, Н. Г. Плетневой.