Метод характеристических функций

Определение 3.4. Характеристической функцией случайной величины ?, называется функция.

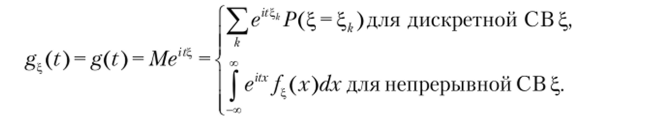
Свойства характеристических функций.

l.g (O) = 1. Очевидно следует из определения. 2-|g (0l.

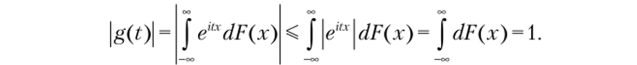
• 3. g (-t) = g (t), так как?(г) = M (costt, + z’sintf;).
• 4. g (t) — равномерно непрерывна.

Доказательство. Действительно,.

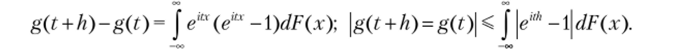
Пусть s — любое положительное число. Выберем постоянную Л достаточно большой, так чтобы J dF (x)<�—. Выберем теперь такое малое h_y

*>^{А 4}

чтобы е'^кх -l| < -^ при х < Л.

А

Тогда g (t + h)-g (t)< je^Lrch-dF (x) + 2 J dF (x), ч.т.д.

• -А |д-|>Л
• 5- gv-ax+bit) = e^itbg_x(at), так как g^t) = Me" ^(ax+h).
• 6. Если х_ь х" — независимые СВ, тогда

у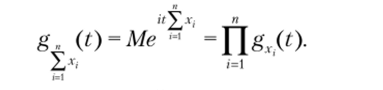

7. Случайная величина Z = 2 X,-, Y не зависит от {X,}, где {X,} —.

f=i.

независимые, одинаково распределенные СВ, Y — целочисленная СВ с производящей функцией cp (.v), g (t) — характеристическая функция СВ X, при любом i. Тогда g₇ = сp (g (t)).

Доказательство. Действительно:

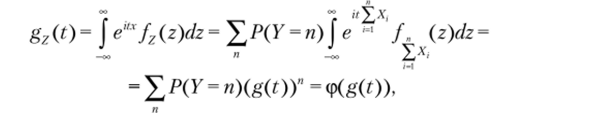
где x_h z — возможные значения СВ Х" Z, i = 1,п.

8. Формула обращения:

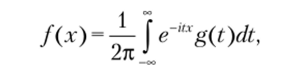
где/(х) — плотность распределения СВ X; g (t) — характеристическая функция СВ X.

Связь характеристической функции с производящей функцией для целочисленной случайной величины ?, задается формулой.

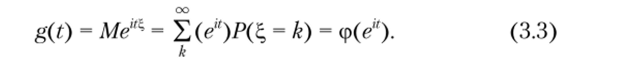
Задание 3.5. Зная производящие функции СВ, распределенных по законам В (п, р), n (k), G (p), cjG (p), Па (г, р)_у ОВ (г, р)_у найдите соответствующие им характеристические функции, используя формулу (3.3).

Задача 3.6. Найти характеристическую функцию, соответствующую закону распределения X — R[a; й].

Решение

ПриХ~й[а;й].

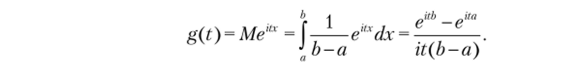
В частном случае, при X ~ Rа а

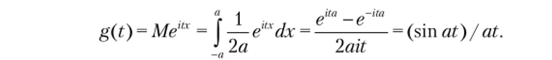
Задание 3.6. Найдите характеристические функции, соответствующие заданным распределениям: а) X — Л'(0, 1); б) X — Х (а, а); в) X — ?(/.);

г) X ~ Коши.

Применение метода характеристических функций для композиции рассмотрим на примере следующей задачи.

Задача 3.7. X и Y — независимые СВ; X — B (n_up), Y ~ В (п₂, р). Найти закон распределения СВ Z = X + Y.

Решение

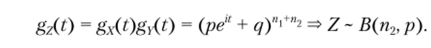
Задание 3.7. Найдите композиции СВ (МХФ) в случаях: а) X — I — Л'(Я|, а,), У — N (a₂, а₂); б) X — я (А.,), Y — л (Х₂).

Связь характеристических функций с моментами MX и DX задается формулами.

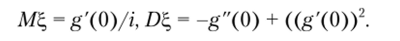
Они выводятся из равенства.

(если СВ ?, имеет абсолютный момент п-го порядка, то g (t) дифференцируема k раз, k < п). Отсюда при k = 1 и 2 Мб, = g'(0)/i, D = М^² — (М^)² = -g" (0) + (g'(О))², или при Ч> = Ing (t) Щ = У'(0), D4> = -^" (О).

Задание 3.8. Получите последние формулы самостоятельно для Мб, I и D6, по формуле (3.4).

Метод характеристических функций состоит в использовании перечисленных свойств характеристической функции.

Приводимые формулировки теорем даны без доказательства и предназначены для практического использования при решении задач.

П

1. Пусть а_и…, а" — постоянные, а,> О, X я,⁼ 1,?,(/), …, g"(7) — ха;

i=i.

П

рактеристические функции. Тогда g (t) = X я,?',(7) — тоже характе;

1−1.

ристичес кая функция.

• 2. Произведение характеристических функций — тоже характеристи чес кая фун кция.
• 3. Единственной характеристической функцией, такой что g (t) = 1 + о (7') при 7 —*? 0, является g (7) = 1.
• 4. Если g (t) — характеристическая функция и она имеет g" (0), то она везде имеет g'(t) и g" (t).
• 5. Теорема Пойя. Еслиg (t) — непрерывна, четна и выпукла книзу при t > 0, g (t) > 1, g (0) = 1, g (t) —> 1 при 7 —>• оо, то g (t) — характеристическая функция.
• 6. Теорема Марцинкевича. Если характеристическая функция g (l) имеет вид е^{Г (1} где l) — полином, то его степень меньше либо равна 2.
• 7. Reg (7) — характеристическая функция, если g (t) — характеристическая функция.
• 8. Если g (t) — характеристическая функция невырожденного распределения и а < 0, то (g (t))" нс является характеристической функцией.
• 9. Из свойства 3 следует, что если характеристическая функция действительна, то четна.
• 10. Если g (t) — характеристическая функция, то |g (7)|² — тоже характеристическая функция.

Рассмотрим примеры на распознавание характеристических функций по свойствам и теоремам. Определим, являются ли характеристическими функциями следующие функции g (t), и если да, то чему они соответствуют.

Пример 3.1. Функция /(7) задана графиком (рис. 3.1).

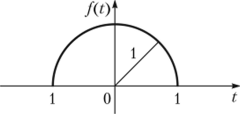
Рис. 3.1. Функция/(7).

Ответ: нет (по теореме 4), так как в точках (-1; 0) и (1; 0) HCTg'(0.

и ?" (?)•.

Пример 3.2. g (t) = exp(t «), а — целое.

Ответ: нет при, а > 2 (по теореме 6); да при, а = 2: X — Л^г(0, V2); нет при, а = 1 (по теореме 9).

Пример 3.3. g (t) = cos²'.

е~" _е" f _е~²" 1 _е²"

Ответ: да, так как cos²(t) = —-1—=—1—-Н — => cos²1 — ха;

^W 2 2 4 2 4.

рактеристическая функция СВ р, где г| задана рядом распределения.

Пример 3.4. g (t) = е ^|(|.

Ответ: да (но теореме 5), это закон Коши.

Пример 3.5. g (t) = е^н" «

Ответ: да, это характеристическая функция СВ X — л (2).

Пример 3.6. g (t) = sin t.

Ответ: нет (но теореме 9).

Пример 3.7. g (t) = (^- + ^-e~^{, 2/2} .

13 3.

Ответ: да (по теореме 6): Y — В (5, 2/3), X — N (0, 1).

Освоение представленной темы требует решения большого числа разных задач на свойства производящей и характеристической функций. Решения большинства задач в основном не представляют трудности, так как объяснены теоретически и на примерах в предыдущих пунктах этого параграфа, поэтому предлагаются для самостоятельного решения. Более сложные приведены с решениями.

Задание 3.9. Найти производящие функции основных распределений дискретного типа и их моменты: а) X = С — const; б) X — В (1,р):

в) X — В (п, р); г) X, — k (L): д) X, — G (p); е) X, — сaG (p); ж) Z, — Па (г, р): з) Z₂ — ОВ (г, р).

т

Задание 3.10. Найти производящие функции СВ L = 2″, Х_; + Ь, где.

i-i.

{X,} — независимые СВ:

• а) X, ~ В (п = 5, р = 0,4), т = 1, а = 3, b = -2;
• б) X, — n (L = 2), т = 3, а = -4, а = 5, а = 1, Ь = -3;
• в) X, — 6'| 1/(/+ 1)|,/= 1. 2, 3, 4; m = 4, а = -1, а = 2, а = -5, а = -3, Ь=-2.

Задание 3.11. Z = ? X_if где У, X, X₂, X" — независимые СВ, име- /-1.

ющие производящие функции, {X,} одинаково распределены.

Найти производящие функции и моменты (MX и DX) СВ Z в следующих случаях:

• а) X ~ В (п = 3, р_х = 0,6), Y~G (p₂ = 0,3);
• б) X, ~ n (L_] = 5), У ~ п (Ь₂ = 4);
• в) X, ~ n (L = 7), У ~ сд (7(/? = 0,4);
• г) X, ~ G (/? = 0,5), У ~ n (L = 2);
• д) Х-, ~ сдС (/?! = 0,1), У~ ?(и = 2,/?, = 0,2);
• е) X, — Па (г = 4, /7, = 0,3), Y~B (n=l, p₂ = 0,3);
• ж) X, заданы рядом распределения

У ~ 71(1).

Задание 3.12. Методом производящих функций найти композиции следующих СВ: а) X ~ л (1,), У — n (L₂); 6) X — В (п_х, р), У ~ В (п₂, р).

Задание 3.13. Используя связь характеристической функции с производящей функцией, найти характеристическую функцию СВ с распределениями, указанными в задании 3.9.

Задание 3.14. Найти характеристические функции следующих распределений: а) X ~ R[a; b|; б) X ~ R-a; а в) X ~ ЕЦ.

Задание 3.16. Найти характеристическую функцию СВ, если: а) X — n (t), У= Зх — 2; б) X — N (a, b)_} У= X — 1; в) X ~R[0; 1], У= 1 — 2 г, г) X ~ В (п, р У= 3-Х.

Задание 3.17. Методом характеристических функций найти моменты (MX и DX) основных распределений задания 3.9, а также для X ~ N (a, b), Х~ R[a] и X~E[L.

Y

Задание 3.18. Z = 2 X,-, где У, X, Х₂,…, Х" — независимые СВ, СВ У.

/-1.

имеет производящую функцию ф ($), СВ {Х_у} одинаково распределены. Методом характеристических функций найти характеристическую функцию СВ Z и ее моменты MZ и DZ в случаях задания 3.9, а также в случаях: а) Х~Х (0, 1), У~ л (/. = 2); 6) Х~ Я[-2; 2], У~ л (А = 3).

Задание 3.19. Методом характеристических функций найти композиции СВ задания 3.12 и следующих СВ: а) X ~ N (a_u а,), У ~ N (a₂, а₂); б) XY~E[L₂.

Задача 3.8. Х" Х₂,…, Х_п — независимые одинаково распределенные СВ и Х_к — /?[—1; 1] для любого k = 1,…, п. Методом характеристических (Ъункпий найти ппелелъный закон паеппелеления СВ S_n L (S'") при.

Решение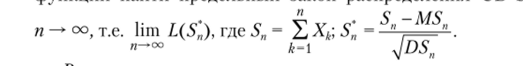

Имеем.

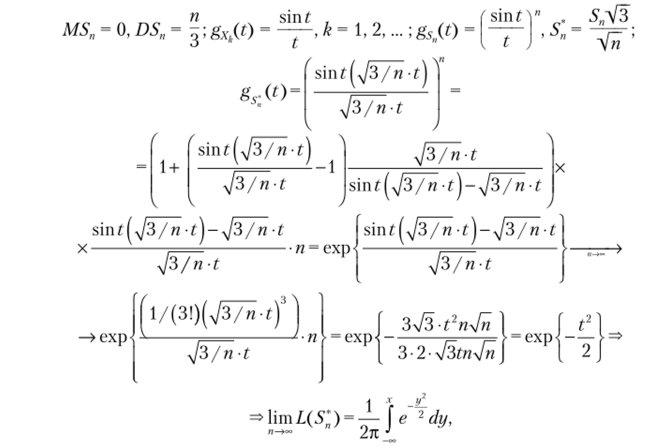
т.е. распределение СВ 5* сходится к А^г(0, 1).

Более трудными и требующими пояснения являются задачи на распознавание возможности для функции быть производящей или характеристической. Приведем примеры решения таких задач.

Задача 3.9. Какие из данных функций являются производящими функциями, и если являются, то каким распределениям они соответствуют:

a) V (s) = 0,5 + 0,4s²; б) V (s) = 0,3 + 0,2s + 0,1s² + 0,4s⁵; в) V (s) = 0,5(1 + exp[3(s — 1)]; r) C (s) = 0,8(0,4s + 0,6)³ + 0,2;

д) V (s) — cxp{2[ 1 + exp (3(s — 1))] - 4}; e) V (s) = s²(0,3s² + 0,7)⁵; ж) C (s) = s²exp[4(s³ — 1) J; з) C (s) = 0,001sV (l — 0,9s³)³.

Решение

• а) C (s) — не производящая функция, так как С (1) ^ 1;
• б) V (s) = (p, v (s) — производящая функция СВ X:

в) V (s) = Фг<5) =.

Y

= 0,5s + 0,5 => X ~ я (3), Y ~ В ( 1, 0,5), Z = X Х" {X,} — одинаково распре;

1=1.

деленные СВ, и У, X, Х₂,…, Х" — независимые СВ и <�р_х (s) = ф_х(5);

г г) У (х) = ф^л) = ф) (ф_Л(л)) — производящая функция СВ Z = X Х".

i = 1.

{X_f} — из свойства 6 производящих функций, где ф_л(х) = (0,4s + 0,6); Ф,<�х) = 0,85 + 0,2 =>X_t~ В (3, 0,4), Y ~ В ( 1, 0,8);

Y

д) V (s) = (p/(s) = ф,(ф_л(х)) — производящая функция СВ Z = X X,.

i = 1.

{X;} — из свойства 6 производящих функций, где ф_л(л) = cxp[3(s — 1)], Ф, X,я (3), Y ~ я (2);

П

е) L = X <*jX; + b, {X,} — одинаково распределенные и независимые.

/ = 1 п

СВ, тогда V (s) =

L(s) = 5″ П ф _v(s) — производящая функция СВ L, где Ф,(х) = (0,3х + 0,7) => Ху — В (5, 0,3), и = 5, а = 2, b = 2;

П

• ж) Z. = X a, Xj + 6, {X,} — одинаково распределенные и независимые
• 1=1 _П

СВ, тогда C (.s) = фу (5) = s^h X ф,(^х) ^— производящая функция СВ L, где.

i= 1.

ф/5) = exp[4(s — 1)] => Ху — я (4), п = 5, а = 3, b = 2;

П

з) 1= х «, Х, + 6, {X,} — одинаково распределенные и независимые.

* = 1 П

СВ, тогда С (5) = фу.(5) = 5* X Ф.;(5) — производящая функция СВ L, где.

0,1 ^{1 = 1}

ф_л-(5) = -—=> X, — сдС (0,1) (сдвинутое геометрическое распределение с параметром р = 0,1), п = 3, а = 3, b = 4.

Задача 3.10. Какие из функций являются характеристическими, и если являются, то каким распределениям соответствуют?

• а) g (t) = 0,1 + 0,2exp (if) + 0,7ехр (8гГ);
• б) g (t) = 0,2[0,3схр (г?) + 0,7] + 0,8схр (г?- 1);
• в) g (t) = ex|)(4;7)cos3f;

r) g (0 = expj ~J~ + ^5U };

Д )g (t) = exp (-100 it);

• е) g (0 ⁼ exp[f (2i — nt);
• ж) g (l) = cos ²t;
• з) g (t) = t,
• 11) g (t) = sinf/f;
• к) g (t) = sinC
• л) g (t) = ехр (-?/4п).

Решение

a) g (t) — характеристическая функция СВ X с рядом распределения.

б) g (t) = g;(0 = ag₂(t) + a2g? t), где a = 0,2; я2 = 0,8; g_x{t) = = 0,3exp (if) + 0,7;g_y(s) = exp{/f- 1}^ЭХ — B (1; 0,3), Y ~ я (1);

B)g (0 = g_y(t) = gxiOgyit), где X и Y — независимые CB, g_x(l) = = exp (4/f); g, (t) = cos31 = 0,5exp (-3/'f) + 0,5exp (3/'f) => X = 4.

Z = X + У;

i)g (0 «g*(0 = ехр[(Ц — l)/3] + 5/7; g._v(/) = exp[(/f — l)/3] => => СВ Xя (1/3); g,</) = 5it => У = 5. Тогда Z = X + У, где ХиУнезависимые СВ;

• д) g® — характеристическая функция СВ X = -100;
• е) g (t) — характеристическая функция СВ X — N (a = 2, b = ~{2п);
• ж) g (t) = gi,(t) = cos t — 0,25[ехр (-1Г) + exp (/Y)| = 0,25ехр (-2/7) + 0,5 + + ехр (2г'Г) => ряд распределения СВ X

з) g (t) = t — нс характеристическая функция, так как |g (/:)| должен быть меньше 1, что здесь невынолнено;

n)g (t) — характеристическая функция СВ X ~ /?[-1; 1]; к) g (l) = sin/ — действительная и нечетная функция, а действительная характеристическая функция обязательно четная;

.'[) g (/) — характеристическая функция СВ X — Д^г(0; 1/Уй).

Методы производящих и характеристических функций широко применяются при доказательстве предельных теорем теории вероятностей.

Предельные теоремы теории вероятностей — общее название групп теорем теории вероятностей, формулирующих условия возникновения определенных закономерностей, проявляющихся при действии большого числа случайных факторов. Они могут выражаться в установлении соответствия между экспериментальными п теоретическими характеристиками усредненных СВ или предельных законов распределения некоторых функционалов СВ, зависящих от их числа.