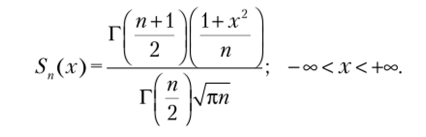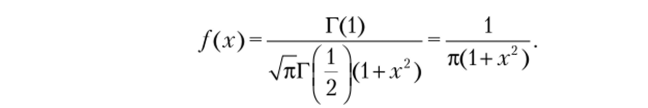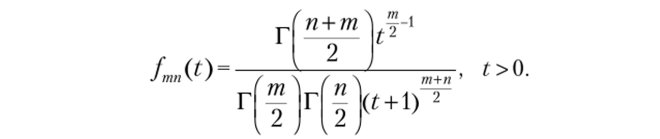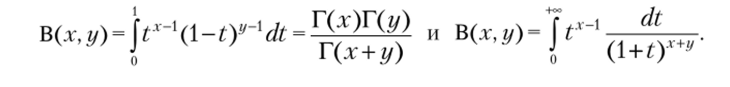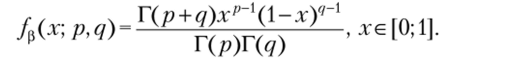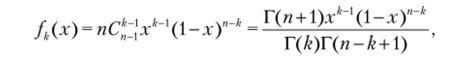Распределение Стьюдента. 
Теория вероятностей

СВ X имеет распределение Стьюдента, если ее плотность распределения имеет вид.

В параграфе 4.6 будет показано, что СВ T = [/J— распределена по закону Стьюдента, если СВ U распределена по нормальному закону Л^г(0,1), а СВ V распределена по закону %²_п; -оо < V< +°о; -оо < U < +оо; U, V — независимые СВ.

При /?=1 закон Стьюдента называется законом Коши с плотностью распределения.

Распределение Фишера

Плотность распределения Фишера есть.

Можно показать, что если СВ X_lt Х₂, Х_т независимы, X =

п ^{, =} 1.

Y], Y₂,…, Y_n независимы, У =? Yf X_h Y_f при всех i = 1,…, n, j = 1,…, т

^j=1 ₂ X.

распределены нормально по закону JV (0, а), тогда СВ Z = ~ имеет распределение Фишера.

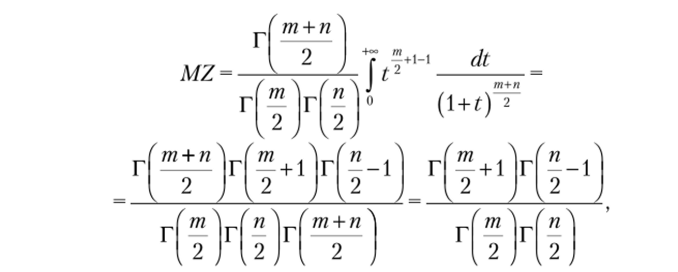
Найдем моменты СВ Z:

так как бета-функция.

В частности, при i = 1 и i = 2 имеем.

Бета-распределение

СВ Z имеет бета-распределение с параметрами р п q (р, q > 0), если ее плотность распределения представляется в виде.

Задача 4.27. Показать, что бета-распределение при р = q = 1 есть равномерное распределение на отрезке [0; 1|.

Решение

 — это плотность равномерного распределения на отрезке [0; 1 ] при х е [0; 11.

Задача 4.28. Пусть СВ Х_и Х₂,…, Х_п, независимы, равномерно распределены па [0; 1), а Х₀₎, Х₍₂₎,…, Х_(п) — упорядоченные в порядке возрастания исходные СВ. Показать, что СВ Х_(к) имеет бета-распределенис (Х₍*) — к-я порядковая статистика).

Решение

Известно, что плотность распределения к-й порядковой статистики f_t(x) имеет вид f_k(x) = nCj; lf (x)F^k '(.r)(1 — F (.x))" *, где /(.г) и F (x) — соответственно плотность и функция распределения СВ X.

В рассматриваемом случае X — 7?|0; 1], поэтому.

т.с. это бста-распрсдслсние с параметрами р = k, q = nk+ (p + q =

= k + п — k + 1 = п + 1).

Задача 4.29. Найти п-й момент т" бета-распределения (m" = MZ").

и дисперсию.

Решение