Неравенства для выпуклых функций

Теорема 2.5. Если функция f непрерывна и выпукла вверх (в нестрогом смысле слова) на отрезке [а, Ь], то справедливо неравенство.

Если же функция / непрерывна и выпукла вниз на отрезке [а, Ь], то справедливо неравенство.

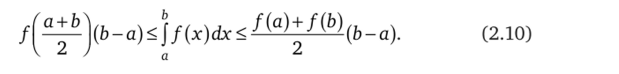
Доказательство. Докажем неравенство (2.10) (неравенство (2.9) доказывается аналогично).

1. Вначале докажем правое неравенство. По условию, функция / непрерывна и выпукла вниз на [а, Ъ], откуда следует, что для произвольной точки х е [а, Ь]

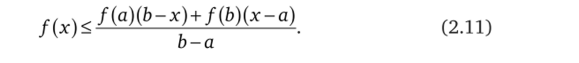
Действительно, это вытекает из справедливости неравенства Йенсена: для любых точек х_1;х₂ е[а, Ь] и любых неотрицательных чисел А,! Д₂, таких что ki + Х₂= 1, выполняется ₁f (x_l') + X₂f (x₂') > jjq +Х₂х₂).

1) — х X — Cl

Положив — -, Х₂ —-, X] - а, х₂ -Ъ, получим неравенство (2.11).

Ъ-а Ь-а

Неравенство доказано.

Замечание 2.11. Доказать левую часть неравенства (2.10) можно было иначе. Сделав замену x = (a + b)/2 + t, докажем неравенство.

Геометрический смысл этого неравенства: ордината точки, лежащей на графике и имеющей абсциссу лг, не больше ординаты точки с той же абсциссой, но лежащей на хорде, стягивающей точки (а;/(а)) и (b;/(b)). Отсюда, интегрируя по отрезку [а, Ь], получаем доказанным правое неравенство в (2.10):

2. Для доказательства левого неравенства (2.10) сделаем замену x = (a + b)/2 + t. Тогда.

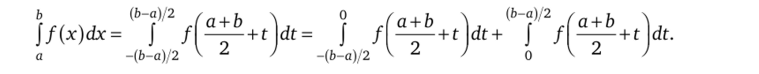
Положив в первом из интегралов z — -t и используя затем неравенство Йенсена, получим.

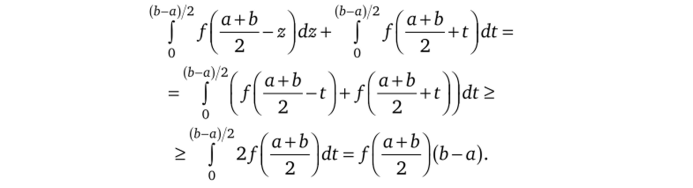
а + Ь.

Если перенести начало координат в точку-, то получим, что л.

нам надо исследовать знак интеграла J g (f)dt, причем про функцию g.

-А

известно, что она выпукла вниз на отрезке [-Л, А] и, кроме того, g (0) = 0. По определению выпуклости, если некоторая функция выпукла вниз на отрезке, то ее график на этом отрезке лежит не ниже касательной, проведенной к графику функции в любой точке отрезка. Проведем касательную в точке с абсциссой t = 0. Очевидно, что интеграл от нее л.

по симметричному отрезку равен нулю. Значит, J g (t)dt >0, т. е.

— л что равносильно левой части неравенства (2.10).

В работе [17, с. 153] приводится интегральное неравенство Йенсена в общем виде. Пусть непрерывная функция q задана на отрезке [а, Ь] и принимает значения из некоторого промежутка X, на котором определена и выпукла вниз функция /. Пусть также на [а, b) задана непрерывная положительная функция р. Тогда справедливо неравенство.

Это неравенство является интегральным аналогом числового неравенства Йенсена (в общем виде).

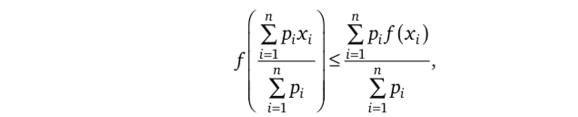
где функция/предполагается выпуклой вниз на некотором промежутке [а, Ь], которому принадлежат точки х_{; p_i — положительные числа (весовые коэффициенты).

Пример 2.1.

Доказать неравенство sinl < j ^°^[1]* dx < 2sinl.

Решение. Заметим, что на отрезке интегрирования функция —-гдопу;

1 + х²

скает оценки — <—у < 1. Умножая последнее неравенство на cosx и инте грируя (применяя утверждение об интегрировании неравенств), получаем.

что и требовалось доказать.

на отрезке [0,1], следовательно, применив к ним неравенство Коши — Буняковского, получаем.

• [1] Пример 2.2 1 Доказать неравенство Jfxexdx< /е-1.о Решение. Воспользуемся интегральным неравенством Коши — Буня-ковского. Рассмотрим функции/(jc) = [х и g (x) = ex. Они интегрируемы