Порядок метода интегрирования и ошибка усечения

Если алгоритм численного интегрирования дает ограниченное решение тестового дифференциального уравнения (10.3.15) для произвольных размеров шага и любого числа шагов при Re А, < 0, то его называют А-устойчивым. Неявные алгоритмы (Эйлера и трапеций) обладают этим свойством. Область абсолютной устойчивости представляет собой часть плоскости q = hX, в которой интегрирование дифференциального… Читать ещё >
Порядок метода интегрирования и ошибка усечения (реферат, курсовая, диплом, контрольная)
Выявим некоторые свойства алгоритмов численного интегрирования (10.3.6)—(10.3.8), представив их в виде обобщенного соотношения.
a{x (tk + h) + a0x (tk) — h[blx'(tk+ h) + 60x'(^)] = 0, (10.3.9).
где значения коэффициентов ал, я0, b{, Ь0 для рассматриваемых алгоритмов приведены в табл. 10.3.2.
Таблица 103.2
Разложим функции x (tk + h) и x'(tk + h) в ряды Тейлора:
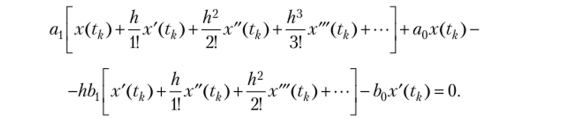
Перепишем последнее выражение в виде ряда по возрастающим порядкам производных:
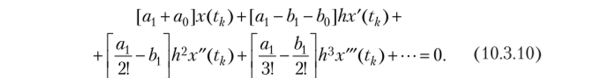
Алгоритм. | аА | «0. | ь | *0. |
Явный алгоритм Эйлера. | i. | — 1. | ||
Неявный алгоритм Эйлера. | — 1. | |||
Неявный алгоритм трапеций. | — 1. | 0,5. | 0,5. |
Подставив в (10.3.10) значения коэффициентов «, из табл. 10.3.2, получим.

Если бы в (10.3.10) содержимое во всех квадратных скобках равнялось нулю, то алгоритм (10.3.9) давал бы в точке tk + к точное решение. Как очевидно из соотношений (10.3.11) и (10.3.12), число первых слагаемых для алгоритмов Эйлера, которое обращается в нуль, ограничено первой производной, а для алгоритма трапеций — второй. Это отражает тот факт, что в алгоритмах Эйлера искомая функция аппроксимирована линейной функцией, в алгоритме трапеций квадратичной функцией или полиномом второй степени. Поэтому говорят, что метод численного интегрирования, базирующийся на формулах Эйлера, имеет порядок р — 1, метод трапеций — порядок р = 2. Погрешность описания искомой функции x (t) определяется неучтенными членами ряда Тейлора, содержащими производные второго, третьего и более высоких порядков. Первый не равный нулю сомножитель в (10.3.11) и (10.3.12) обозначим ср+1 и назовем ошибкой усечения. Для алгоритмов Эйлера ср+1 = с2 = |½|, для алгоритма трапеций ср+] = с3 = 1/12. В приведенных выше примерах при использовании алгоритма получены более точные результаты, чем при использовании алгоритмов Эйлера. Причина этого в большем значении порядка р интегрирования и меньшей ошибке усечения ср+| алгоритма трапеций.
Устойчивость методов интегрирования. Помимо порядка метода интегрирования и ошибки усечения важным свойством алгоритмов численного интегрирования является их численная устойчивость, под которой понимают способность с ростом числа шагов сохранять в ограниченных пределах локальную методическую ошибку и ошибку округления при значении шага h -> 0.
Как уже отмечалось выше, погрешность расчета численным методом в момент Ц можно оценить как разность между точным и приближенным вычисленным значением.

где ем к — ошибка неточности самого алгоритма, называемая методической ошибкой, или ошибкой отсечения. Эта ошибка, как было показано выше, обусловлена ограничением числа членов ряда (например, Тейлора), заложенного в алгоритме численного интегрирования; е0 k — ошибка округления, обусловленная ограниченным количеством разрядов или конечной длиной машинного слова.
Для сравнения точности алгоритмов используют понятие локальной ошибки (методической и округления) в пределах одного (обычно первого) шага. Методическая ошибка и ошибка округления имеют тенденцию нарастать в процессе вычисления от шага к шагу.
Для выявления численной устойчивости алгоритма используют дифференциальное уравнение.

точное решение которого имеет вид х = x (0)exp (Ai). При этом константа X может быть действительным или комплексным числом. Для устойчивого дифференциального уравнения Re А, < 0. Оценим численную устойчивость алгоритмов Эйлера и трапеций.
Явный, а л г о р и т м Эйлера. 11одставив в прямую формулу Эйлера (10.3.3) производную из уравнения (10.3.15), получим 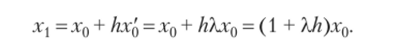
Сделаем такую же подстановку на следующем шаге алгоритма: 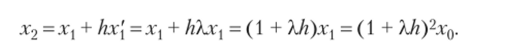
Продолжив эту процедуру в пределах п шагов, найдем.
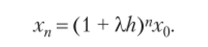
Чтобы результат был ограниченным при п—«оо, необходимо выполнение следующего соотношения:
Для нахождения области, в которой удовлетворяется условие (10.3.16), обозначим hX=q=u +jv и подставим в (10.3.16). Получим.

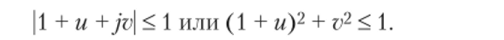
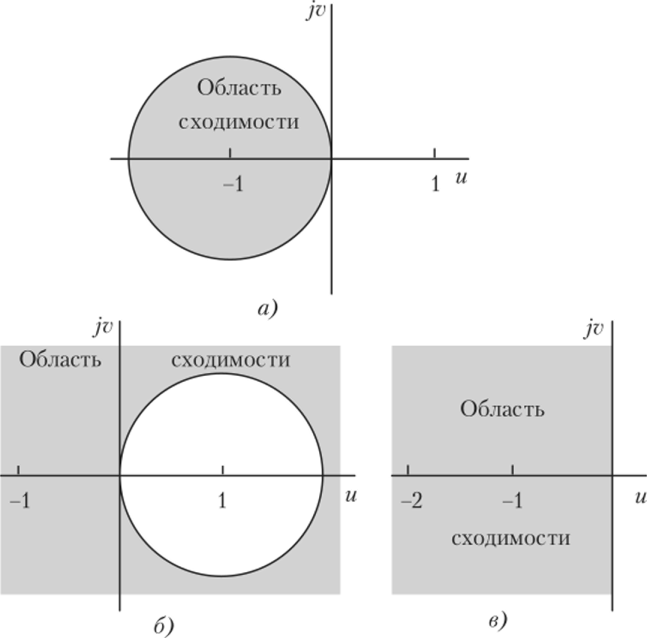
Последнее выражение описывает область устойчивости, которая лежит внутри круга (при и = v = 1) с центром в точке (-1, 0), т. е. в круге, сдвинутом относительно начала координат (рис. 10.3.2, а). Полученный результат можно использовать следующим образом. При Re^ < 0 выбирается шаг h так, чтобы значение q = hX соответствовало точке внутри круга. В этом случае численный метод интегрирования будет устойчив, т. е. значение функции x (t), вычисленное на п-м шаге при п —" оо, будет конечным.
При больших значениях |AJ длина шага должна быть малой для гарантированной устойчивости.
Пример. В табл. 10.3.3 приведены результаты решения уравнения х' = -х при х0 = 1 для трех случаев:
- • шаг интегрирования h = 0,1; значение q находится внутри области устойчивости. Результаты численного интегрирования незначительно отличаются от точного решения схр (-?);
- • шаг интегрирования h = 2; значение q соответствует границе области устойчивости. В этом случае решение осциллирует, но нс нарастает;
- • шаг интегрирования h — 3, значение q находится вне области устойчивости. Результат нарастает и осциллирует, хотя точное решение должно уменьшаться.
Таблица 1033
Шаг п | Решение. | |||
точное. | при h = 0,1. | при h = 2. | при h = 3. | |
0,9048. | 0,9. | — 1. | — 2. | |
0,8187. | 0,81. | |||
0,7408. | 0,729. | — 1. | — 8. | |
0,6703. | 0,6561. | |||
0,6065. | 0,5905. | — 1. | — 32. | |
0,5488. | 0,5314. | |||
Неявный, а л г о р и т м Э й лера. Для этого алгоритма область численной устойчивости описывается следующим соотношением:
При и = v = 1 она лежит вне окружности единичного радиуса (рис. 10.3.2, б), центр которой находится в точке (1,0).
Рис. 10.3.2. Устойчивость методов интегрирования:
а — явный метод Эйлера; б — неявный метод Эйлера; в —
метод трапеций.
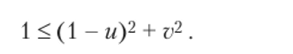
Неявный алгоритм трапеций. При п —"оо условие устойчивости имеет вид.
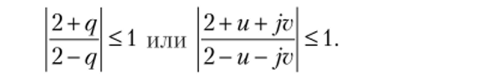
Его можно свести к неравенству и —" 0, из которого следует, что границей устойчивости является мнимая ось, а областью устойчивости является левая полуплоскость (рис. 10.3.2, в). Отметим, что, но сравнению с неявным алгоритмом Эйлера область устойчивости уменьшилась. При этом метод интегрирования имеет больший порядок. Следовательно, более высокий порядок р метода может сопровождаться уменьшением устойчивости.
Другой особенностью алгоритма трапеций является то, что он дает устойчивый отклик для устойчивых решений уравнения (10.3.15), у которых ReA- 0.
Следует иметь в виду, что выполнение условий устойчивости для численного метода не является свидетельством правильности результатов расчета, а означает только то, что любая ошибка при вычислениях не увеличится на последующих шагах. Один из путей обеспечения правильности результатов для выбранного размера шага состоит в использовании алгоритмов с наивысшим порядком р. Однако более высокий порядок метода может сопровождаться уменьшением устойчивости, как это обнаружилось в алгоритме трапеций.
Если алгоритм численного интегрирования дает ограниченное решение тестового дифференциального уравнения (10.3.15) для произвольных размеров шага и любого числа шагов при Re А, < 0, то его называют А-устойчивым. Неявные алгоритмы (Эйлера и трапеций) обладают этим свойством. Область абсолютной устойчивости представляет собой часть плоскости q = hX, в которой интегрирование дифференциального уравнения (10.3.15) при Re А, < 0 дает ограниченный результат для любого числа шагов. Как было показано выше, неявный алгоритм Эйлера абсолютно устойчив во всей левой полуплоскости. Большинство цепей, встречающихся на практике, является устойчивым. Для линейной цепи это означает, что действительные части корней характеристических уравнений отрицательны. Поэтому для тестового уравнения (10.3.15) имеют в виду решение при Re А. < 0.