Математическая модель процесса экстракции

В результате продольного перемешивания при движении каждой из фаз происходит выравнивание концентраций по высоте колонного экстрактора и снижение разделительной способности аппарата. В связи с этим становится важным учет продольного перемешивания в математической модели структуры потоков при составлении общей математической модели процесса экстракции.

Основной вклад в продольное перемешивание вносит турбулентная составляющая. Механизм турбулентного перемешивания имеет стохастическую природу, поэтому при описании структуры потока целесообразно применить вероятностную схему [6].

Мысленно выделим из стохастического ансамбля одну частицу и рассмотрим ее возможное поведение, полагая, что остальные элементы ансамбля ведут себя аналогично. Для простоты рассмотрим одномерную задачу. Представим вероятностную схему блуждания частицы, предполагая, что она может перемещаться в прямом и обратном направлении. Разобьем систему на ячейки (рис. 29.22), размер которых соответствует средней длине свободного пробега частиц / в стохастическом движении.

Пусть Ат — среднее время пребывания частицы в ячейке. Тогда точки на шкале времени г = кАт (к = 1,2,3)можно рассматривать как моменты перехода частицы из одной ячейки в другую. Предположим, что за каждый переход частица перемещается в соседнюю ячейку либо в прямом, либо в обратном направлении. Вероятность перехода из j-й в (/+1)-ю ячейку равна р, вероятность обратного перехода изу-й в (j-1)-ю ячейку равна q. Так как прямой и обратный переходы представляют собой взаимоисключающие альтернативы, то р + q — 1. Кроме того, так как на случайное турбулентное поле скоростей накладывается направленное поле скоростей вынужденного движения потока, то р > q. Обозначим через f (x, т) вероятность того, что блуждающая частица из точки х = 0 в момент г = 0 в результате п переходов окажется в момент т_п = пАт в ячейке с координатой х.

Рис. 29.22. Вероятностная схема переходов частиц между ячейками (р — вероятность перехода изу-й в (/+/)-к> ячейку; q — вероятность перехода изу'-й в (/-/)-«о ячейку Переход из ячейки в ячейку эквивалентен перемещению на среднюю длину пробега /. Если через т обозначить число переходов в прямом направлении, а через к — в обратном, то общее число переходов п = т + к, а координата х должна быть определена как х = Цт-к). Нетрудно представить, что вероятности прямого и обратного переходов будут р^т/п и q = к/п = (пт)/п при условии, что п достаточно велико.

Рассмотрим теперь, какова вероятность события, при котором частица в некоторый момент г + Дг окажется в ячейке с координатой xj. Очевидно, что эта вероятность должна зависеть от вероятности событий, при которых в предыдущий момент времени частица окажется в соседних ячейках, а также от вероятности перехода частицы из соседней ячейки в рассматриваемую. Указанную взаимосвязь событий можно представить следующим соотношением:

Из обеих частей этого равенства вычтем f (x, т) и с учетом того, что р + q = 1, получим:

Далее, полагая, что функция f (x, т) дифференцируема по х, г, пользуясь ее разложением в ряд Тейлора и ограничиваясь первыми членами, получим с учетом малости I:

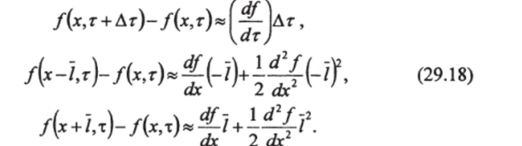
После подстановки (29.18) в (29.17) находим:

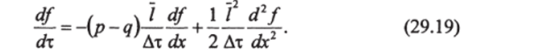
Член (p-q)i/AT имеет смысл средней скорости и направленного движения, так как.

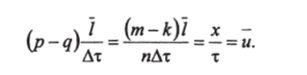
/Дт = D имеет смысл коэффициента турбулентного переме Член —/² 2.

шивания. Если учесть, что / - средняя длина пробега частицы, а отношение //Лг = v есть эквивалент средней скорости стохастического движения частиц, то коэффициент D будет по структуре аналогичен коэффициенту диффузии D = vl/2.

Уравнение (29.19), записанное относительно вероятностной характеристики f (x, т), известно в кинетической теории диффузии как уравнение Фоккера-Планка. Оно применено без учета физической природы частиц. Это могут быть мономолекулы, их ассоциаты или достаточно крупные частицы диспергированной фазы, находящиеся в стохастическом движении.

В рассуждениях вероятностная функция f (x, г) отнесена к одной блуждающей частице. При переходе к характеристике ансамбля частиц указанная функция отождествляется со статистической функцией меченых частиц, выражаемой через их концентрацию. Поэтому приведенное к концентрации трассера уравнение Фоккера-Планка принимает вид.

Это уравнение диффузионной модели и в равной мере применимо для описания как сплошной, так и диспергированной фазы в экстракторе при условии определяющего влияния турбулентности на продольное перемешивание.

Обратим внимание на то, что при выводе уравнения (29.19) мы приняли, что / - является величиной бесконечно малой. В принципе / - конечная величина, характеризующая средний масштаб турбулентности.

В секционных аппаратах этот масштаб может достигать размера расстояний между тарелками. В таком случае участок, соизмеримый со средней длиной пробега частицы, может рассматриваться как зона идеального смешения, а модель приобретает форму системы ячеек с сосредоточенными параметрами, связанных между собой прямыми и обратными протоками.

Ячеечная модель с обратными протоками или, как ее еще называют, рециркуляционая модель (рис. 29.23), может рассматриваться как конечно-разностная схема диффузионной модели, которая в пределе стремится к диффузионной при условии, что число ячеек п —> со. Величину / = //Z, называют относительной долей обратного потока. Система уравнений, приведенная к безразмерной форме, для однофазной ячеечной модели с обратными потоками имеет вид:

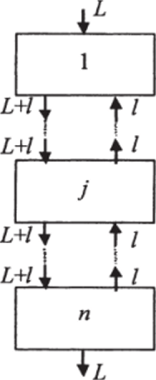
Рис. 29.23. Структура гидродинамических потоков в рециркуляционной модели (L — прямой поток через ячейку; / - рециркуляционный поток).

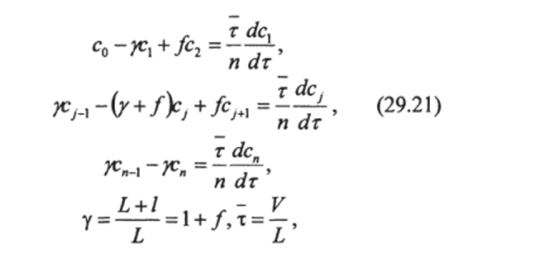
где V — объем фазы, м³; L — объемный расход, м³/ч; п — число ячеек; С₀— концентрация вещества на входе в аппарат, индексы 1,2 J, п — номера ячеек.

Связь между параметрами диффузионной и рециркуляционной моделей устанавливается из следующих соображений. На основании разложения, аналогично (29.18), имеем и

Подставив (29.22) и (29.23) в (29.20), находим:

Поскольку / = Н/п, где Я — высота аппарата, и соответственно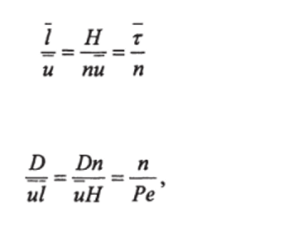

где (Ре = uH/D) — число Пекле.

Преобразуем уравнение (29.24) с учетом этих замен:

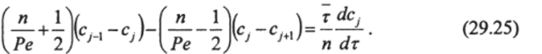
Преобразуем второе уравнением системы (29.21) к виду.

Приравнивание соответствующих составляющих в левых частях уравнений (29.25) и (29.26) приводит к равенству:

По соотношению (29.27) рассчитывают величину обратного потока/по значению Ре, которое в свою очередь определяют с помощью известных методов для диффузионной модели. Величина обратного потока однозначно определяется через значение Ре только тогда, когда фиксировано число ячеек. В ряде случаев (например, для насадочных аппаратов) число ячеек заранее не определено, и требуется дополнительная информация для нахождения ли/ Если же речь идет о формальной конечно-разностной аппроксимации характеристик диффузионной модели, то для обеспечения приемлемой точности достаточно принять п ?10 при условии, что п/Ре > ½. Если Ре > 20, характеристики диффузионной модели приближаются к модели идеального вытеснения.

К достоинствам ячеечной модели с обратными потоками (помимо ее гибкости) следует отнести удобство алгоритмизации расчетов на ЭВМ, обусловленное дискретностью ее структуры.

При описании процесса экстракции в колонном аппарате используется двухфазная ячеечная модель с обратными потоками с учетом массообмена между фазами. Условия квантования на ячейках принимаются одинаковыми для обеих фаз. Различия в интенсивности продольного перемешивания в фазах учитываются через величины долей обратных потоков/, и /в (рис. 29.24).

Рассмотрим материальный баланс по потокам фаз с учетом массопередачи. Для этого рассмотрим у-ю ячейку в обеих фазах (рафината G и экстракта Ь).

Межфазный поток из рафината в экстракт.

где К_0у - объемный коэффициент массоперсдачи (ч¹), приведенный к движущей силе для фазы G; Az = Н/п — высота участка идеального смешения, м, эквивалентная шагу квантования системы; - свободное сечение в колонне, м²; l//(cj) — функциональная зависимость для изотермы равновесия.

Материальный баланс потоков для фазы рафината j-й ячейки имеет вид.

для фазы экстракта соответственно имеем.

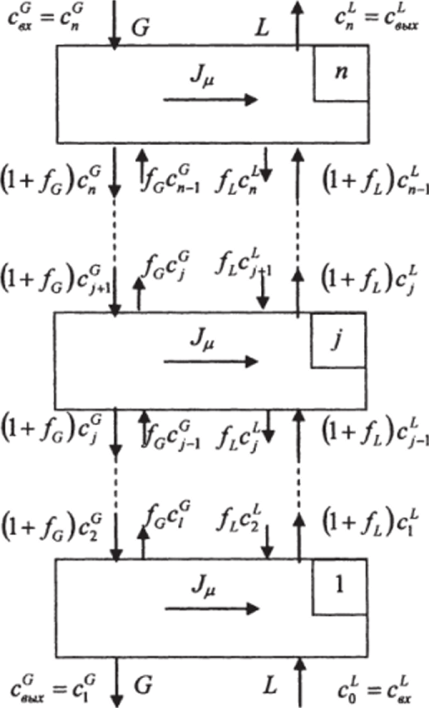
Рис. 29.24. Структура потоков в двухфазной модели экстрактора.

где G и L — нагрузки по фазам рафината и экстракта соответственно, м³/ч;Ус и f_L- доли обратных потоков в фазах.

Введем обозначения:

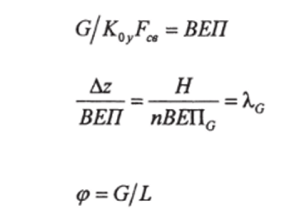
• — высота единицы переноса в фазе G:
• — число единиц переноса, приходящихся на ступень (ячейку) смешения;
• — соотношение между нагрузками фаз рафината и экстракта.

Рассмотрев по аналогии (29.28) и (29.29) материальный баланс потоков с 1-м по п-ю ячейки экстракционного аппарата, с учетом введенных обозначений получаем полное описание системы в соответствии со структурой рис. 29.24:

Для 1 -й ячейки:

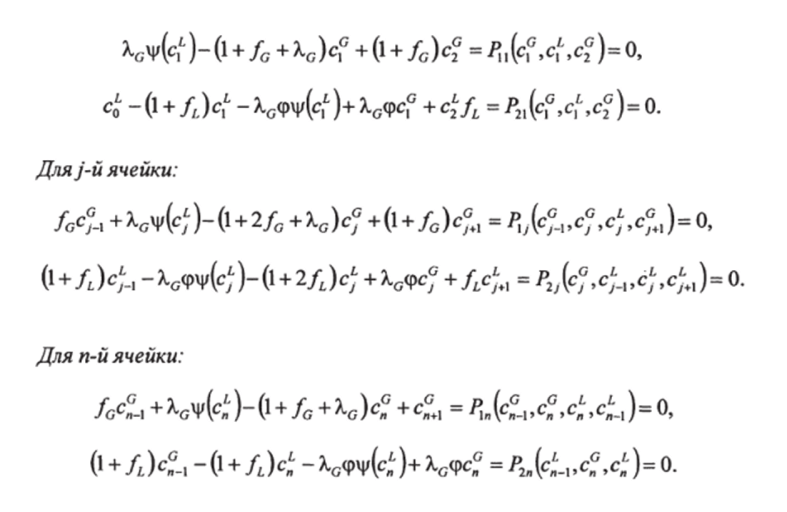
Вектор-столбец.

определяет совокупность величин, характеризующих профиль концентраций по высоте экстрактора в обеих фазах.

Полное математическое описание задает перечень параметров, подлежащих расчетному определению. Это — характеристика изотермы равновесия у/(с^Л), коэффициенты и число ячеек п. Расчет указанных параметров в зависимости от гидродинамического режима экстрактора осуществляется на основании экспериментальных данных, полученных непосредственно на аппарате.

Методика и техника эксперимента для получения полного набора этих данных приведена в работе [6].