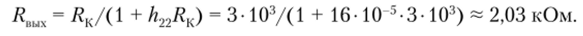Входное и выходное сопротивления усилителя

Из схемы замещения усилителя (см. рис. 2.3.7) входное сопротивление усилителя напряжения на частотах, при которых можно пренебречь сопротивлением конденсатора С, равно.

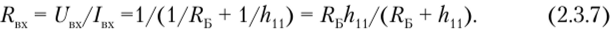
В реальном эксперименте для измерения R_BX в качестве источника входного напряжения используют источник с постоянной амплитудой U_Bxm синусоидального сигнала. Последовательно с источником включают резистор Д_дн6с изменяемым сопротивлением.

Сначала устанавливают /?_лоб = 0, рекомендованное значение R_tt, U_Bxm < <^их тмакс ¹¹ измеряют С"_ых Затем увеличивают R_ao6 до значения R^, при котором выходное напряжение уменьшится в два раза. Очевидно, что при этом Z"_x = r;,"_v

Выходное сопротивление усилителя напряжения по схеме рис. 2.3.6 при тех же условиях для сопротивления конденсатора С₂ и С_п равно.

В реальном эксперименте для измерения Z_Ublx устанавливают линейный режим усилителя, отключают резистор нагрузки и измеряют (/_выхт. Затем в качестве резистора нагрузки включают резистор R_ao6 с изменяемым сопротивлением. Уменьшают или увеличивают его сопротивление до R'_ao6, при котором напряжение на нем будет равно [/_выхт/2.

Пример 2.3.1.

На рис. 2.3.1 приведена схема усилительного каскада на БТ с общим эмиттером. Используя входную и выходную ВЛХ транзистора на рис. 2.3.8, рассчитать сопротивление резистора Й_Г), при котором рабочая точка, но постоянному току будет находиться на середине линейных участков выходной и переходной ха;

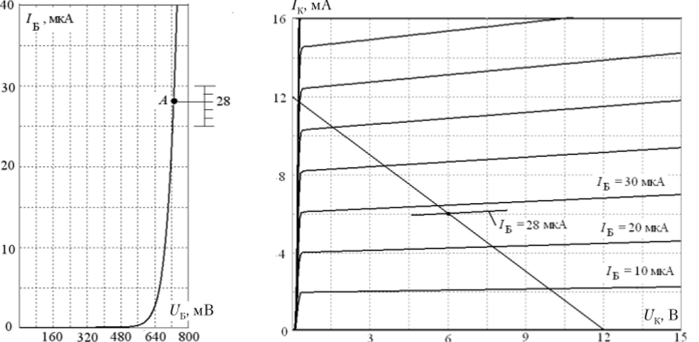
Рис. 2.3.8. ВАХ транзистора к примеру 2.3.1 (MicroCAP).

рактеристик, если Е_к = 12 В и R_K = 1 кОм. Определить также коэффициент усиления К_и, входное R_uy и выходное /?_вых сопротивления усилителя. Значения h-параметров транзистора: /?, = 1,5 кОм, h_2] = 200, h._n = 6,7• 10 ⁵ См.

Решение

На семействе выходных ВЛХ транзистора проводим линию нагрузки, соответствующую Е_к = 12 В и R_K = 1 кОм. Рабочую точку по постоянному току выбираем в середине линии нагрузки. Координаты этой точки соответствуют значениям U_Kll = 6 В, /_{к п} = 6 мЛ, /_{Б п} = 28 мкЛ.

Для полученного тока базы сопротивление базового резистора согласно формуле (2.3.2) равно.

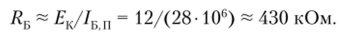
Коэффициент усиления по напряжению определяем из формулы (2.3.6), учитывая, что сопротивление нагрузки R_u —?

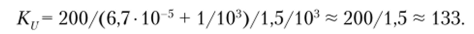
Входное сопротивление определяем по формуле (2.3.7):

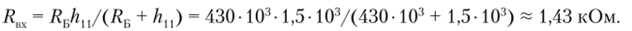
Выходное сопротивление определяем по формуле (2.3.8):

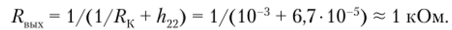
Упражнение 2.3.2*.

Определить коэффициент усиления по напряжению ненагруженного усилителя (см. рис. 2.3.1) при R_l{ —* °о и R_K = 1кОм (//-параметры транзистора заданы в табл. 2.3.1).

Таблица 2.3.1

К упражнению 2.3.2*.

Пример 2.3.2

Определить доступный коэффициент усиления по напряжению К_илост = = U_BbJX/E_BX усилителя на БТ (см. рис. 2.3.1), если R_BT = 1кОм, R_b = 5кОм, R_K = = ЗкОм, h_u = 1 кОм, h._n = 20, h₂₂ = 50 -10^-6 См и /г₁₂ = 0.

Решение

Доступный коэффициент усиления, но напряжению K_UjkOCTt учитывающий падение напряжения на внутреннем сопротивлении источника сигнала, определяется следующим образом.

Входное сопротивление усилителя.

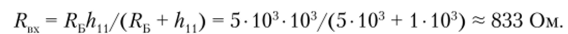
Коэффициент усиления по напряжению (из формулы (2.3.6)).

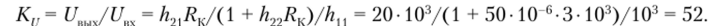
Входное напряжение усилителя равно U_BX = E_BXR_BX/(R_BT + R_BX). Поэтому.

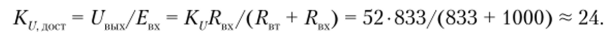
Пример 2.3.3.

В усилителе на БТ (см. рис. 2.3.1) БТ имеет й-парамстры: h_n = 900 Ом, й₂₁ = = 50, h₂₂ = 16−10 ⁵ См. Определить выходное напряжение и выходное сопротивление, если ?_вх = 8 мВ, R_m = 300 Ом, R_K = 3 кОм, R_b h 1.

Решение

Входное напряжение.

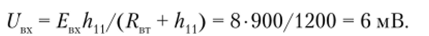
Выходное напряжение.

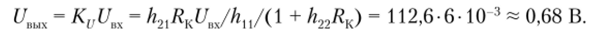
Выходное сопротивление.