Приближенные методы решения

В зависимости от соотношения геометрического размера и длины электромагнитной волны X принято рассматривать три области пространства L:

• 1) квазистационарную (ближнюю) — L/X 1;
• 2) резонансную — L/X& 1;
• 3) квазиоптическую (дальнюю) —1/Х" 1.

В ближней области решение задач базируется на методах электрои магнитостатики, в резонансной — на точных методах. В квазиоптической области используются приближенные методы. К числу приближенных методов решения задач электродинамики относят методы геометрической оптики, волновой (физической) оптики, краевых волн, геометрической теории дифракции. В перечисленной последовательности приближенные методы позволяют получить более точное решение.

Метод геометрической оптики является предельным при решении волновой задачи, когда длина волны X стремится к нулю. Это означает, что здесь не учитывается волновой характер поля. Данный метод применим при определении электромагнитного поля (чаще всего при решении задач на отражение электромагнитных волн), когда размеры отражающего тела и минимальный радиус кривизны его поверхности велики по сравнению с длиной волны. Кроме того, необходимо, чтобы источник поля находился на достаточно большом расстоянии от поверхности тела.

Основные положения метода геометрической оптики состоят в том, что электромагнитная энергия распространяется внутри лучевых трубок; поток энергии внутри каждой лучевой трубки постоянен; амплитуды векторов поля в каждой точке пространства определяются из постоянства потока энергии внутри лучевой трубки; фазы электромагнитных колебаний в каждой точке пространства определяются длиной пути от источника до точки наблюдения и изменяются вдоль луча линейно; если через точку наблюдения проходит несколько лучевых трубок, то результирующее поле определяется как геометрическая сумма полей всех составляющих.

Следует иметь в виду, что понятие лучевой трубки применимо, когда амплитуды векторов поля и параметры среды мало изменяются на расстоянии длины волны, что в однородной среде лучи являются прямыми линиями, а в неоднородной — плавными кривыми, что перераспределение энергии между соседними лучевыми трубками отсутствует и векторы Е и Я перпендикулярны лучу.

В геометрической оптике предполагается, что поле в точке наблюдения определяется значениями его векторов в тех точках отражающей поверхности или волнового фронта поля источника, из которых лучи приходят в данную точку. Таким образом, метод геометрической оптики дает решение только в «освещенной» области пространства. В тени он «не работает».

Метод волновой оптики (физической оптики), в отличие от предыдущего, учитывает волновой характер электромагнитного поля и базируется в соответствии с принципом Гюйгенса на представлении поля точечного источника в виде волновой функции.

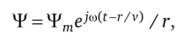
где ^VF — любая составляющая вектора поля; со — круговая частота; г — расстояние до точки наблюдения; v — скорость волнового процесса.

Этот метод применим при тех же ограничениях, что и метод геометрической оптики, т. е. для больших, гладких тел, когда точка наблюдения находится на достаточном расстоянии от источника. Однако метод волновой оптики позволяет определять электромагнитное поле и в области геометрической тени (при использовании этого метода области тени за объектом не существует, что реально и наблюдается при эффекте дифракции).

Амплитуда напряженности электромагнитного поля в точке наблюдения определяется как геометрическая сумма колебаний. Математическая формулировка метода волновой оптики с точностью до постоянного фазового множителя ехр (/л/2) совпадает с формулой скалярного интеграла Кирхгофа. В то же время метод волновой оптики совпадает с методом геометрической оптики в том отношении, что значения волновой функции реально могут быть заданы точно только в пределах освещенного (полем источника) участка волнового фронта, а в теневой области полагаются равными нулю. Это же обстоятельство не позволяет в интеграле Кирхгофа задать точно значения всех подынтегральных функций и использовать этот интеграл в качестве точного решения задач электродинамики.

Метод краевых волн является развитием метода волновой оптики применительно к телам, поверхность которых имеет изломы, ребра и т. д. Он используется при тех же ограничениях, что и предыдущий метод, только позволяет несколько ослабить требования по соотношению размеров тела, радиуса кривизны его поверхности и расстояния до точки наблюдения и длины электромагнитной волны.

Суть метода краевых волн состоит в том, что, в отличие от предыдущих методов, где на теневой части тела либо волнового фронта источника поле принималось равным нулю, поле источника на теневой поверхности вблизи краев тела (ребер, изломов) отлично от нуля. Это отличие связано с появлением вблизи границ тела дополнительной (возмущенной) составляющей поверхностного тока, вызванной влиянием края тела.

Таким образом, более точное задание волновой функции на фронте волны источника либо более точное задание подынтегральных функций в интеграле Кирхгофа позволяет получить более точное решение электродинамической задачи.

Метод геометрической теории дифракции представляет собой развитие метода геометрической оптики применительно к решению задач дифракции электромагнитных волн на больших (по отношению к длине волны) телах сложной геометрической формы. Он также базируется на предположении, что энергия распространяется внутри лучевых трубок с теми же особенностями, что и в методе геометрической оптики, однако, в отличие от метода геометрической оптики, кроме падающих, отраженных и преломленных лучей вводятся в рассмотрение дифрагированные лучи. Метод геометрической теории дифракции позволяет получить результаты при решении задач дифракции на телах сложной конфигурации, которые хорошо согласуются с результатами точного решения и результатами экспериментальных исследований. Однако применение этого метода достаточно затруднительно, когда необходимо определить поле в области каустики (область, куда приходит очень большое число лучей — например, фокальная область). В этих случаях применяются специальные методы, которые здесь не рассматриваются.

Вопросы для самопроверки

• 1. Какова размерность вектора Пойнтинга?
• 2. В каких случаях в электромагнитном поле может отсутствовать вихревая или потенциальная составляющая?
• 3. Чем отличаются плоские волны от Н-волн?
• 4. В чем заключается различие между линейной и эллиптической поляризацией?
• 5. Чему равно волновое число?