Формирование понятия совместного действия

Второй уровень сложности задач «на процессы» связан с ситуацией «совместного действия». Решение этих задач осложнено следующими факторами:

• 1. Числом «участников»: действует не одна сила, а две и более.
• 2. Характером взаимодействия сил: помогают друг другу или противодействуют.
• 3. Временем включения действующих сил: одновременно или в разное время включились участники в совместное действие.
• 4. Дополнительными отношениями основных величин: кроме отношений величины с двумя другими величинами, связанными с данной действующей силой, появляются отношения между общими и частными значениями каждой величины. Так, общая скорость (У₀) теперь является не только функцией общего времени (Т₀) и суммарного (общего) «продукта» ($₀), но и функцией частных значений скоростей (V,): представляет собой алгебраическую сумму частных скоростей.

Эти факторы входят в состав условий, которые необходимо учитывать при решении задачи. Это значит, что все они должны стать ориентирами для учащихся, войти в содержание ориентировочной основы общего приема решения.

Для этого надо было организовать усвоение этих условий.

Методика работы с данной системой отношений была в принципе той же, что и при формировании понятий об основных величинах и их отношениях в ситуации одного участника процесса.

Вначале мы организовали усвоение отношений между суммарным «продуктом» как результатом действия всех участников и частными «продуктами», получаемыми отдельными участниками процесса. Особое внимание при этом уделялось характеру участия: помогает другим участникам процесса или противодействует им.

На этапе материализованных действий использовались, как и раньше, полоски бумаги и отрезки прямой, которые удобны для моделирования усваиваемых отношений. Так, например, при решении задачи — «В колхозе работали три бригады. Две бригады собирали фрукты, а третья продавала их. Известно, что первая бригада собрала 800 кг, вторая 700 кг, а третья продала 900 кг. Сколько фруктов осталось в колхозе?» — учащиеся последовательно откладывали на полоске бумаги результаты действий первой и второй бригады (в определенном масштабе), обозначали их числовую величину, а затем отрывали часть полоски, моделирующую «продукт» действий третьей бригады.

На этапе материализованных действий одновременно готовился переход на внешнеречевой этап. С этой целью учащимся предлагалось работать не только с моделями, но и записывать данные в речевой форме с использованием символов для обозначения основных величин. Анализ условия задачи они вели в соответствии с данным им планом (карточка № 2), который имел следующий вид:

Карточка № 2^[1][2]

Учащиеся записывали под соответствующими номерами ответы на все эти вопросы и в результате получали краткую запись задачи. Так, вышеприведенная задача была записана следующим образом:

• 1) 3 уч.
• 2) Вместе (т. е. одновременно)
• 3) I и II помогают, III против
• 4) Ничего
• 5) Sj = 800 кг, S₂ = 700 кг, S₃ = 900 кг
• 6) S_G = ?

После решения нескольких задач на нахождение общего и частных «продуктов» с использованием моделей учащиеся переходили на этап внешнеречевых действий и работали с опорой только на записи.

В таком виде было решено еще несколько задач, после этого мы переходили к задачам, требующим понимания отношений между общей и частными скоростями. Мы не ставили себе цели довести все действия до умственной формы, поэтому обучение закончили на внешнеречевом этапе.

При формировании понятия об отношении скоростей отдельных участников процесса и общей скорости специальное внимание уделялось не только характеру взаимодействия участников (помогают или мешают друг другу), но и временным отношениям их действий: участники действуют одновременно или разновременно.

Учащиеся должны были понять, что общая скорость на том или ином временном интервале может быть получена путем суммирования частных скоростей только при условии одновременности действия участников процесса. Для этого мы предлагали задачи такого типа:

«Тремя бригадами дорога построена за 10 дней. Первая бригада работала только первые 3 дня и строила по 200 м/день. После этого приступили к работе вторая и третья бригады. Вторая бригада строила 300 м/день, а третья — 350 м/день. С какой скоростью строилась дорога после того, как приступили к работе вторая и третья бригады?».

На материализованном этапе усвоения мы в обязательном порядке требовали от учащихся изображения всех данных на схеме. Вот одна из схем к приведенной задаче:

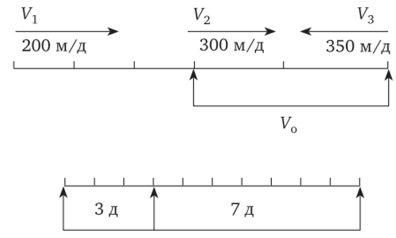
Рис. 3.11.

На схеме, составленной испытуемыми, легко видеть, что в первые три дня дорога строится со скоростью, равной 200 м/день, а в следующие 7 дней дорога строится со скоростью 650 м/день.

Виды взаимодействия участников были усвоены учащимися фактически при анализе отношений между общим и частными «продуктами» процесса, поэтому при работе со скоростями это не вызывало у них никаких затруднений.

Испытуемые легко дифференцировали случаи, когда скорости следует суммировать, а когда вычитать одну из другой. Например, ситуации: а) движение парохода против течения и б) движение двух поездов навстречу друг другу.

Отношения между скоростями формировались также на уровне внешнеречевого этапа действия.

Последними отрабатывались отношения между общим временем процесса и временем действия отдельных участников. Под общим временем (Г₀) понималось время, необходимое для всего «продукта» (5₀), когда участники действуют одновременно.

В этом случае общее время равно времени действия каждого участника. При разновременном действии участников время, затраченное на изготовление продукта, мы назвали суммарным (Г_с). Его отношение к общему продукту позволяет получить не общую, а среднюю скорость. Например, допустим, известно, что в изготовлении деталей приняли участие три бригады. Первая бригада работала 5 часов со скоростью 10 деталей в час; вторая работала 10 часов со скоростью 20 деталей в час; третья бригада работала 5 часов со скоростью 20 деталей в час. В данном случае общая скорость равна 50 деталям в час (У₀ = V, — + У₂ + + У₃ = 10 д/ч + 20 д/ч + 20 д/ч = 50 д/ч).

Суммарное время (Т_с) изготовления деталей равно 20 ч: Т_С = Т₁ + Т₂ +

+ т₃.

Для получения общего времени (Г₀) нам надо предварительно узнать величину общего продукта (Б₀) и поделить его на общую скорость (У₀). В данном случае общий «продукт» может быть получен как сумма частных «продуктов», которые, в свою очередь, могут быть получены как произведения соответствующих частных скоростей на соответствующее частное время (У_а • Т_х) + (У₂ • Т₂) + (У₃ • Г₃) = 50 д + 200 д + 100 д = = 350 д. Общее время, следовательно, равно 7 часам (Г₀ = 5₀: У₀ = 350 д:: 50 д = 7). Это означает, что если бы все три бригады работали одновременно, то они затратили бы на изготовление деталей 7 часов. Средняя скорость (У_с) равна 17,5 д/час (У_с = Б₀: Т_с — 350 д: 20 ч).

Понятие общего времени и времени суммарного дифференцируется не так легко: испытуемые пытаются получить его по аналогии с общей скоростью и общим «продуктом», т. е. путем суммирования частных затрат времени. Только моделирование величин и их отношений позволяет показать, что общее время имеет место только тогда, когда «продукт» изготовляется с общей скоростью, т. е. одновременно всеми участниками процесса.

Не все учащиеся смогли сразу перенести понятие об отношениях между основными величинами процесса, усвоенное на задачах с одним участником, на ситуацию «совместного действия». Но достаточно было испытуемым один раз поработать на моделях, чтобы понять идентичность отношений между величинами, относящимися или к одному из участников совместного действия, или ко всем вместе.

Для обобщения отношений в ситуации совместного действия мы в конце обучения предлагали учащимся абстрактные качественные задачи типа: «Имеется какое-то совместное действие двух „участников“? По каким данным можно узнать ½?».

На этом этапе обучения все испытуемые справлялись с такими задачами легко. Вот обычно как протекало их решение:

Испытуемый. По Б₂ и Т₂ делением, вот (пишет): У₂ = 5₂: Т₂. Экспериментатор. А если этих данных нет, то можно ли по другим данным узнать У₂1

Испытуемый. По У₀ и У₁… вот (пишет): У₂ = У₀ — 1?₁.

Отработка понятий, связанных с ситуацией совместного действия, заканчивалась на внешнеречевом этапе. Испытуемые не только успешно решали задачи, но и сами составляли их, причем про себя. Это говорит о том, что они уже могли действовать в умственной форме. Всего на речевом этапе каждый испытуемый выполнил 10—13 заданий разного вида.

В результате проведенного обучения учащиеся усвоили таким образом все элементы и все отношения между ними, которые составляют основное содержание общего приема решения задач на «процессы». Мы полагали, что после этого он не вызовет у наших испытуемых затруднений, что впоследствии полностью подтвердилось.

• [1] Определить:
• [2] Сколько участников действует? 2. Начинают и кончают они вместе или нет? 3. Как они действуют: а) помогают? б) противодействуют? 4. Что известно в задаче об общих величинах (50, Т0, У0)? 5. Что известно о частных величинах (Б, Т, V,)? 6. Что требуется узнать в задаче?