Контрольная серия эксперимента

Данная серия эксперимента была предпринята с целью выяснения, насколько правильно были нами выделены основные компоненты умения доказывать. Контрольные задания испытуемым предъявлялись вместе с готовыми чертежами. Это устраняло те трудности, которые могли быть связаны у испытуемых с построением чертежа. В основе построения лежат специальные умения, которые мы у наших испытуемых не формировали.

Контрольные задания, предложенные испытуемым состояли в доказательстве трех следующих теорем: 1) теорема о равенстве двух треугольников по двум сторонам и углу, заключенному между ними; 2) теорема о равенстве углов с соответственно перпендикулярными сторонами; 3) теорема о равенстве вертикальных углов.

Результаты выполнения контрольных заданий Количественная сторона результатов выполнения контрольных заданий испытуемыми была следующей.

Было предложено 50 теорем и 10 задач. Все теоремы были доказаны правильно. Все задачи были решены верно.

Приведем протокольные записи, отражающие типичный ход решения контрольных задач и доказательство теорем испытуемыми этой группы.

Предлагается доказать теорему о равенстве треугольников по двум сторонам и углу между ними.

Теорема формулируется следующим образом: «Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой» (рис. 4.1).

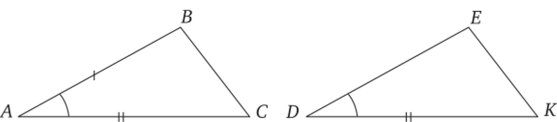
Рис. 4. /.

Испытуемый Ш. Л. (читает условие теоремы и первый пункт правила: «Выдели то, что дано в условии»). Даны два треугольника и еще сказано, что у них соответственно равны стороны.

Экспериментатор. Какие?

Испытуемый. АВ равно DE, а АС равно DK, и углы между ними равны: угол ВАС равен углу EDK (читает второй пункт правила: «Укажи, что требуется доказать»). Доказать надо, что треугольники равны.

Экспериментатор. Дальше.

Испытуемый (читает третий пункт правила: «Назови все признаки, по которым можно доказать то, что требуется». Перечисляет признаки равенства). Здесь накладывать надо треугольники по первому или по второму признаку.

Экспериментатор. Прочти следующий пункт правила.

Испытуемый (читает четвертый пункт правила: «Укажи, как еще эти признаки могут быть заданы („скрыты“) в условии»). Здесь первый признак и второй. Они даны, если равны какие-нибудь элементы фигур, равенство которых требуется установить, а здесь у треугольников равны стороны и углы.

Экспериментатор. Все стороны равны?

Испытуемый. Нет, только две стороны одного треугольника соответственно равны двум сторонам другого треугольника. Еще углы между этими сторонами равны. Здесь не сказано только про ВС и ЕК, но они тоже будут равны, так как между двумя точками можно провести только одну прямую линию.

Экспериментатор. Читай следующий пункт.

Испытуемый (читает шестой пункт правила: «Назови тот признак, который нужно использовать для доказательства»): Здесь по первому и по второму признаку решать.

Экспериментатор. Дальше.

Испытуемый (читает седьмой пункт правила: «Объясни, почему ты считаешь, что этот признак есть в условии»). Эти треугольники надо наложить друг на друга так, чтобы равные стороны и углы у них совпали: АВ совпадет полностью с ПЕ, значит, точка В совпадет с точкой Е, точка А с точкой С, угол ВАС совпадет с углом ЕОК, АС совпадет с ОК.

Экспериментатор. Почему?

Испытуемый. Так как АС равно ОК. Точки С и К совпадут. У треугольников совпали все вершины, значит, и все стороны будут равны.

Экспериментатор. Будут ли равны стороны ВС и ЕЮ

Испытуемый. Они тоже совпадут по второму признаку равенства, так как у этих отрезков совпали конечные точки, а между двумя точками можно провести только одну прямую. Эти треугольники полностью совпали между собой, значит, они равны.

Приведем пример решения задачи испытуемым М. Ш. Особенность этой задачи заключалась в том, что установление равенства выступало в качестве средства ее решения.

Экспериментатор. Правильно. А нельзя ли решить эту задачу без продолжения ОН?

Испытуемый (пауза). Можно, тоже по четвертому признаку. Только я не знаю, где взять второй угол прямой (пауза). Тут нужно вычитать из суммы двух углов. Углы АОК и НОС составляют в сумме 90°.

Экспериментатор. Почему?

Испытуемый. Угол КОН — прямой. Он входит в развернутый угол АОС. Из угла АОС вычитаем угол КОН, получаются два угла: КОА и НОС. В сумме они равны 90°. Теперь решать по четвертому признаку: от КОН отнять угол ВОН и останется угол КОВ, потом от суммы углов АОК и НОС отнять угол НОС, останется угол АОК. От двух равных мы отнимаем по два равных и остаются два равных угла.

Приведем пример доказательства теоремы о равенстве вертикальных углов.

Теорема формулируется так: «Вертикальные углы равны между собой».

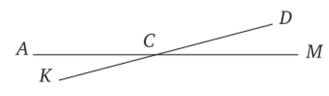
Рис. 4.2.

Испытуемый (читаетусловие теоремы, затем первый пункт правила). Вертикальные углы даны. Еще «скрыто» даны развернутые и смежные углы (показывает на чертеже, затем читает второй пункт правила). Надо доказать равенство вертикальных углов, например: АСК и ВСМ, по признакам равенства надо решать. Можно скажу?

Экспериментатор. Пожалуйста.

Испытуемый. От угла КСО мы отнимаем угол АСО и остается угол ОСМ. Тут четвертый признак. От двух равных (развернутых) мы отнимаем один и тот же угол и остаются равные углы.

зательства. Так было, например, при доказательстве теоремы о равенстве углов с соответственно перпендикулярными сторонами, а также при решении задачи на доказательство. Причем в последнем случае, как это видно из приведенного примера, был дан вариант доказательства, связанный с использованием дополнительного построения, которому мы испытуемых не обучали.

Как видно из приведенных примеров, «пробы и ошибки» при выполнении контрольных заданий отсутствовали. Испытуемые действовали уверенно. Процесс доказательства носил сознательный характер и на всех этапах протекал фактически безошибочно.

Результаты данной части контрольного эксперимента свидетельствуют о достаточности формирования указанных компонентов умения для доказательства теорем, представленных и в форме задач, и в тех формулировках, в которых они обычно даются в школьных учебниках геометрии.

Следует отметить, однако, что сформированное умение применялось лишь к теоремам и задачам на доказательство равенства. В связи с этим необходимо было выяснить возможность более широкого переноса умения доказывать, в частности на теоремы и задачи на доказательство какого-либо другого вида. В известной мере решение этого вопроса подготовлено результатами, полученными в исследованиях, посвященных формированию начальных геометрических понятий. Как известно, усвоение геометрических понятий состоит прежде всего в усвоении соответствующих действий и операций с признаками данного понятия. В исследовании Н. Ф. Талызиной [14] было показано, что при формировании системы однородных геометрических понятий вместе с овладением первыми понятиями данной системы учащиеся овладевают также и определенными операциями мышления, которые затем используются при усвоении последующих понятий этой же системы. Причем перенос этих операций в зависимости от ряда условий может происходить на разном уровне, однако он всегда есть и его наличие приводит к ускоренному усвоению последующих понятий этой системы. В результате достигается более быстрое по сравнению с обычным обучением формирование системы геометрических понятий. Результаты данного исследования давали нам основание предполагать, что подобного рода перенос может иметь место также и при доказательстве теорем. Мы проверили возможность переноса умения доказывать теоремы и задачи, сформированные при доказательстве равенства, на теоремы и задачи на доказательство параллельности.

После выполнения контрольных заданий на равенство испытуемым разъяснили, что доказанные ими теоремы на равенство треугольников, а также вертикальных углов и углов с соответственно перпендикулярными сторонами они могут рассматривать теперь как особые признаки равенства треугольников и углов.

С целью выяснения возможности переноса умения доказывать теоремы на равенство на теоремы и задачи другого вида испытуемым, без дополнительного обучения, были предложены следующие теоремы на параллельность: 1) теорема о равенстве острых и тупых углов с соответственно параллельными сторонами; 2) теорема о равенстве углов с соответственно параллельными сторонами 2(1, если один из них острый, а другой тупой; 3) теорема о параллельности биссектрис двух острых углов с соответственно параллельными сторонами.

Кроме указанных теорем испытуемым было предложено еще четыре задачи на доказательство. Установление параллельности прямых в них явилось или целью решения или его средством. Следует отметить, что отдельные из этих задач требовали для своего решения использование ранее доказанных теорем на равенство.

Напомним, что у испытуемых специально формировались понятия о накрест лежащих углах, соответственных и односторонних. Кроме этого, им давалось также определение параллельности прямых: две прямые параллельны, если они лежат в одной плоскости и при своем продолжении не пересекаются.

Перед выполнением данного вида контрольных заданий испытуемые получали карточку с признаками параллельности.

В качестве признаков параллельности нами были взяты следующие: 1) две прямые параллельны, если они лежат в одной плоскости и при своем продолжении не пересекаются; 2) две прямые параллельны, если при пересечении их третьей прямой накрест лежащие углы равны; 3) две прямые параллельны, если при пересечении их третьей прямой соответственные углы равны; 4) две прямые параллельны, если односторонние углы в сумме составляют 180°; 5) две прямые параллельны, если они перпендикулярны с третьей прямой.

Результаты выполнения испытуемыми второй группы контрольных заданий на определение параллельности были следующими.

Испытуемые в целом довольно успешно справились с контрольными теоремами и задачами на установление параллельности прямых линий: в 63 случаях из 70 ими было дано правильное доказательство и лишь в семи случаях испытуемые с доказательством теорем и решением задач не справились.

Приведем протокол, отражающий типичный ход выполнения контрольных заданий данного вида.

Была предложена задача: «Даны два прямоугольных треугольника ОСП и МОК, имеющие общую вершину О. Известно, что катет ОС треугольника ОСО вместе с катетом ОК треугольника МОК образуют одну прямую линию. Доказать, что катеты СО и МК параллельны между собой».

Испытуемый Б. Т. (.читает условие задачи). Здесь будут катеты СИ и МК параллельны. Решать можно по второму признаку. Здесь накрест лежащие углы будут равны.

Экспериментатор. Какие?

Испытуемый. Углы РСО и ОКМ — накрест лежащие. За секущую мы берем СК. Сказано, что СО и ОК составляют одну прямую линию. Накрест лежащие углы будут равны, так как они оба прямые. Значит, СО будет параллельна МК. Еще можно по четвертому признаку решать.

Экспериментатор. Пожалуйста.

Испытуемый. Тут СО и МК будут параллельны, если продолжить, например, СО и поставить букву X. Тогда получаются односторонние углы: ХСО и МКО, они в сумме составляют 180°.

Экспериментатор. Правильно. А как еще можно решить задачу?

Испытуемый. Еще? Если только по пятому признаку, больше я не знаю.

Экспериментатор. Попробуй.

Испытуемый. СК — секущая и она образует прямые углы с СП и МК, значит, она к ним перпендикулярна. СП будет параллельна МК.

Как видно из приведенного примера, к выполнению контрольных заданий на параллельность испытуемые подходили так же уверенно, как и к заданиям на равенство.

В целом ряде случаев ими были даны не один, а два и более вариантов доказательства.

Выполняя доказательство, испытуемые все время ориентировались на признаки параллельности, используя их в качестве критерия наличия параллельных прямых. Теоремы и задачи, в которых параллельность выступала не в качестве искомого, а как средство его обнаружения, тоже затруднений у испытуемых не вызывали. Важно отметить, что их не смущали задания, выполнение которых требовало использования ранее доказанных теорем на равенство. Теоремы такого рода испытуемые теперь рассматривали как дополнительные признаки равенства, истинность которых уже не требует повторного доказательства.

Хорошие результаты выполнения испытуемыми второй группы заданий на параллельность дают основание рассматривать их как следствие переноса умения доказывать с теорем на равенство на теоремы и задачи другого вида, основным содержанием которых являлось установление параллельности прямых линий.

Следует, однако, отметить, что выполнение контрольных заданий на параллельность не всегда протекало легко и гладко. В ряде случаев доказательство теорем и решение задач вызывало у испытуемых известные затруднения.

Анализ ошибочных доказательств показал, что причина невыполнения заданий отдельными испытуемыми связана главным образом с некоторой недоработкой у них понятия геометрического равенства. Так, в частности, у этих испытуемых было обнаружено не только отсутствие умения заменять ту или иную фигуру другой, равной ей фигурой, но и непонимание возможности такой замены.

Ошибочное выполнение контрольных заданий в семи случаях можно объяснить также тем, что доказательство некоторых теорем требовало использования таких признаков равенства, которые нами не выделялись и не отрабатывались специально.

С испытуемыми, не выполнившими контрольные задания, были проведены дополнительные занятия, направленные на формирование недостающих у них знаний и умений. Затем им снова были предложены те контрольные задания, которые ранее вызывали у них затруднения. При повторном предъявлении испытуемые справились с ними успешно.

Как указывалось выше, все задачи и теоремы, которые испытуемые выполняли в контрольной серии опытов, были затем для сравнения предъявлены учащимся VI и VII классов. Результаты выполнения контрольных заданий учащимися VI и VII классов представлены в табл. 4.1.

Таблица 4.7.

Как видно из таблицы, учащиеся VI класса лишь в 15 случаях из 60 правильно выполнили контрольные задания на равенство и в 35 случаях из 70 справились с теоремами и задачами на параллельность.

Напомним, что испытуемые экспериментальной группы задания на равенство выполнили правильно в 60 случаях из 60, а задания на параллельность — в 63 из 70. Что касается учащихся VII класса, то, как видно из табл. 3.1, результаты выполнения ими контрольных заданий того и другого вида примерно такие же, как и у учащихся VI класса.

С заданиями на параллельность учащиеся VII и особенно VI класса справились несколько успешнее, чем с контрольными заданиями на определение равенства фигур. Объяснить это можно, с одной стороны, тем, что тема «параллельные прямые» в курсе геометрии VI класса изучается в конце учебного года и, следовательно, все знания, связанные с данной темой, еще не были учащимися забыты. С другой стороны, это может быть объяснено и тем, что в курсе геометрии выделяются признаки параллельности. И хотя они специально не отрабатываются, однако при доказательстве конкретных теорем на параллельность и решении задач на доказательство они используются.

Результаты проведенного эксперимента говорят, таким образом, о преимуществе нашей методики перед школьной. Это нашло свое выражение не только в том, что с доказательством теорем и решением задач наши испытуемые справились значительно успешнее учащихся VI и даже VII класса, но и в том, что для формирования у наших испытуемых умения доказывать теоремы на равенство и на параллельность потребовалось затратить примерно в два раза меньше времени, чем это предусмотрено школьными программами при изучении соответствующих разделов.

Результаты, полученные в данном эксперименте, дают нам также основание считать, что выделенные нами компоненты действительно составляют содержание умения доказывать.

В данном исследовании были выделены компоненты умения доказывать теоремы и решать задачи на доказательство только одного вида. Анализ других разделов геометрии позволит выделить в каждом из них аналогичные компоненты. А это значит, что можно научить всех учащихся самостоятельно доказывать большинство геометрических теорем.

Как показало исследование, полная отработка таких компонентов не является всегда необходимой. Усвоение испытуемыми названных компонентов умения доказывать теоремы на определение равенства фигур оказалось достаточным, чтобы испытуемые затем без дополнительного обучения успешно справились с теоремами и задачами на установление параллельности прямых линий. Имевший место в нашем эксперименте перенос умения доказывать теоремы одного вида на теоремы и задачи другого вида объясняется общностью логической структуры признаков понятий, которые являются основой выделения данных теорем и задач в отдельные виды. Содержание понятий «равенство» и «параллельность» совершенно различно, однако логическая структура действия подведения под эти Понятия одинакова. Чтобы установить, равны или нет те или иные геометрические фигуры, нужно проверить, обладают ли они хотя бы одним из признаков равенства. Аналогично, чтобы определить, параллельны или нет две прямые линии, надо также проверить, обладают ли данные прямые хотя бы одним из признаков параллельности. Соответственно одинаковыми были метод развертывания условий, а также последовательность их анализа.

Общность структуры умений, которые использовались при доказательстве теорем того и другого вида, и обусловила, таким образом, описанный нами выше перенос.

При изучении геометрии школьниками очень важно сформировать у них общие приемы доказательства геометрических теорем. Однако формированию такого рода приемов в школьной практике не уделяется почти никакого внимания. Учащиеся не видят ничего общего в доказательстве различных теорем. Каждая теорема воспринимается ими как новая, доказательство которой нужно только заучить. Именно этим и объясняется то, что при изменении чертежа теоремы или введении новых буквенных обозначений учащиеся затрудняются воспроизвести ранее заученное доказательство.

Проведенный эксперимент показал возможность формирования у учащихся общих приемов геометрического доказательства. Выделение общих признаков равенства, формирование действия подведения под понятие «равенство», а также действия «развертывания» условий обеспечивают свободную ориентировку испытуемым в теоремах на установление равенства геометрических фигур. Теоремы данного вида наши испытуемые воспринимали как простые задачи на применение признаков равенства. В школьной же практике общие признаки равенства не только не отрабатываются, но даже и не выделяются. Если учесть также и то обстоятельство, что многие теоремы на равенство относятся в учебниках к различным разделам курса геометрии, то станет ясно, почему учащиеся воспринимают различные теоремы указанного вида как не имеющие друг с другом ничего общего.

Естественно, что в результате многократного столкновения с теоремами того или иного вида у учащихся стихийно формируются приемы доказательства теорем. Однако возникают они при таком способе формирования очень медленно, чаще всего оказываются неполноценными и, как показало данное исследование, формируются далеко не у всех учащихся.

Поскольку в условиях теорем и задач на доказательство признаки искомых геометрических явлений задаются в «скрытом» виде, большое значение приобретает овладение учащимися третьим компонентом умения доказывать действием «развертывания» условий, благодаря которому достигается выявление искомых признаков. Полнота и тщательность отработки данного компонента значительно повышает качество выполнения геометрического доказательства.

Исследование показало необходимость формирования у учащихся не только умения «развертывать» условия в общем виде, но и вести поиск в определенном направлении.

В эксперименте была показана возможность формирования у учащихся умения вести «направленный» поиск в процессе осуществления геометрического доказательства. Последнее достигалось путем отработки действия «развертывания» с опорой на «поисковые области». Такая отработка позволяет рационализировать процесс «развертывания», что приводит к значительному уменьшению времени поиска искомых признаков.

Успех в проведении геометрического доказательства зависит, таким образом, не только от того, насколько правильно раскрыто действительное содержание умения доказывать, но и от того, насколько полно это содержание усвоено. Так, успешное выполнение нашими испытуемыми контрольных заданий объясняется прежде всего тем, что, выделив три основных компонента умения доказывать, мы сделали в то же время каждый из них специальным объектом усвоения.

Взаимосвязь и последовательность применения отдельных компонентов в процессе доказательства задавалась в нашем эксперименте специальным правилом, которым испытуемые руководствовались, выполняя контрольные задания.

В ходе дальнейшего исследования это правило должно быть раскрыто более полно.

Основной же задачей нашей последующей работы является выделение условий формирования более общих приемов, обеспечивающих самостоятельный подход учащихся к более широким классам геометрических теорем и задач на доказательство.

Несомненно, что решение этой задачи позволит повысить уровень геометрического мышления учащихся, а также даст возможность получить больший эффект как в отношении качества обучения, так и в смысле сокращения времени, необходимого для обучения геометрии.