Минимизация сложных высказываний

Совершенные дизъюнктивная и конъюнктивная формы применяются при выполнении задач минимизации сложных логических высказываний. Под минимизацией понимают такие действия над данной формулой, в результате которых получают новую формулу, содержащую меньшее количество букв.

Рассмотрим один из способов минимизации, при котором используется геометрический подход [9].

Представим себе куб (рис. 3.14, а), вдоль ребер которого осуществляется движение. Направления движения указаны стрелками Л, В и С. Исходным пунктом служит вершина куба, к которой направлены стрелки (если пользоваться понятиями аналитической геометрии, можно сказать, что начало системы координат находится в этой вершине).

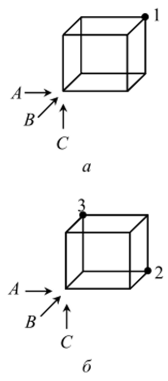
Рис. 3.14. Куб: а) х = АВС;

Как попасть из исходной точки в другую вершину, например в ту, которая обозначена цифрой /? Путь к вершине / проходит последовательно вдоль ребер, совпадающих с направлениями стрелок А, В и С (разумеется последовательность может быть и другой).

Рассмотрим еще две вершины: 2 и 3 (рис. 3.14, б). В вершину 2 можно попасть, последовательно двигаясь по направлениям А и В. Отсутствие движения по направлению С обозначаем как С. Вершине / соответствует тройка букв А, /?, С, вершине 2 — АВС, а вершине 3 — АВС.

б) х = АВС + АВС

Если дано произвольное сложное высказывание, написанное в СДНФ, в которую входят трехбуквенные произведения, то каждому произведению соответствует определенная вершина куба. Справедливо и обратное: каждой вершине куба соответствует произведение трех простых высказываний.

Например, высказывание.

изображается точками /, 2, 3 и 4 куба (рис. 3.15, а), а точкам куба на рис. 3.15, б соответствует формула.

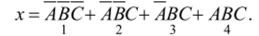
Рассмотрим куб на рис. 3.15, в, на котором отмечены две точки: У и 2. Этим точкам соответствует сложное высказывание.

В этом сложном высказывании можно вынести АВ за скобки, т. е. произвести слияние по букве С:

Для сложного высказывания.

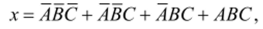
изображенного на рис. 3.15, б, можно выполнить слияние по С (для первого и второго произведений) и по А (для третьего и четвертого произведений):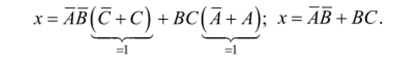

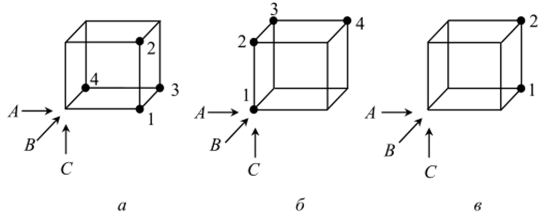
Рис. 3.15. Куб: а) х = АВС + АВС + АВС + АВС; б) х = АВС + АВС + АВС + АВС; в) х=АВС+АВС.

На основании рассмотренных примеров можно написать правило минимизации сложных трехбуквенных высказываний, написанных в СДНФ:

• 1. Отмечаем вершины куба, которые соответствуют трехбуквенным произведениям.
• 2. Если какие-либо две из отмеченных вершин лежат на одном ребре, для этих вершин вместо двух трехбуквенных произведений записываем одно двухбуквеннос (производим слияние по букве, для которой соответствующее ей направление совпадает с направлением ребра, к которому принадлежат отмеченные вершины).

На практике могут встречаться сложные высказывания, отдельные произведения которых содержат по четыре буквы. И в этом случае может быть применен геометрический подход к минимизации сложных высказываний.

Как известно, куб имеет три измерения: ширину, высоту и глубину, которые обозначим буквами А, В и С, соответствующими простым высказываниям. Поэтому введем в рассмотрение искусственный куб с четырьмя измерениями (рис. 3.16, а). Четвертое измерение получается при движении внутрь от вершин большого куба к соответствующим вершинам малого куба.

Рассмотрим использование четырехмерного куба для изображения сложных высказываний. Пусть имеется высказывание.

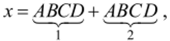
которое дано в СДНФ. Четырехбуквенные произведения соответствуют точкам 1 и 2. И в этом случае движение совершается по стрелкам А, В и С; кроме того, поскольку в четырехбуквенном произведении содержится буква Д имеется движение от достигнутой вершины большого (внешнего) куба внутрь к соответствующей вершине малого (внутреннего) куба. Если в четырехбуквенном произведении содержится буква Д то никакого движения внутрь нет.

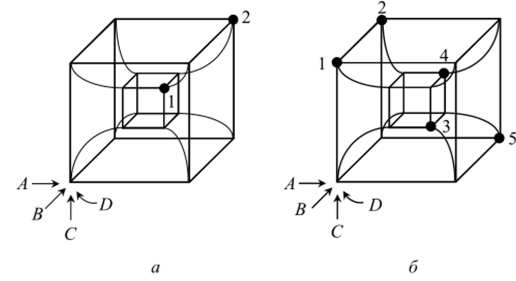
Рис. 3.16. Четырехмерный куб: а) х = A BCD + ABCD; б) x = ABCD + ABCD+ABCD + ABCD + ABCD.

И в этом случае существует обратное соответствие: вершинам четырехмерного куба соответствуют строго определенные четырехбуквенные произведения. Например, кубу на рис. 3.16, б соответствует логическая формула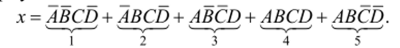

Правило минимизации сложных логических высказываний, содержащих четырехбуквенные произведения, заключается в следующем:

1. Отмечаются вершины куба, которые соответствуют четырехбуквенным произведениям.

2. Если какие-либо две из отмеченных вершин лежат на одном ребре (здесь в понятие «ребро» включается и мысленная линия, которая соединяет соответствующие вершины двух кубов), то для такого ребра вместо двух четырехбуквенных произведений пишется одно трехбуквенное (выполняется слияние в направлении буквы, для которой соответствующее ей направление совпадает с ребром с отмеченными вершинами).

Если сначала произвести слияние по букве Д то получится обыкновенный трехмерный куб.

В качестве примера минимизации рассмотрим сложное высказывание которому соответствует куб на рис. 3.17, а.

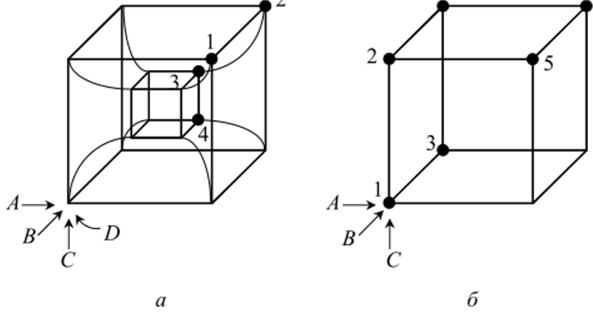
Рис. 3.17. Куб: а) х = ABCD+ ABCD + ABCD + ABCD; б) х= АВС + АВС+АВС+АВС + АВС + АВС.

Минимизация осуществляется с использованием ребер, соединяющих отмеченные вершины. На рис. 3.17, а используются два ребра между точками 1−2 и 3−4. Для этих ребер можно записать.

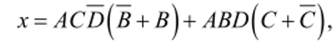
что по существу представляет собой слияние по буквам В и С. Окончательно получаем л = АСD + ABD.

Несмотря на простоту геометрического подхода к минимизации, в некоторых случаях конечный результат зависит от выбора ребер, по которым производится слияние. Рассмотрим для примера сложное высказывание, представленное следующей таблицей истинности:

Тому же высказыванию, записанному в СДНФ,.

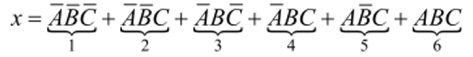
соответствует куб на рис. 3.17, в.

Выполнив слияние по ребрам 1−3, 2−4, 5−6, получим.

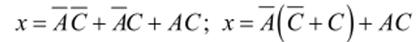
или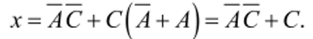

Если выполнить слияние по ребрам 1−2,2−5, 3−4 и 4−6, то получим.

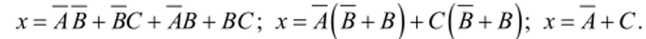
В первом случае слияние выполнено по трем ребрам, а во втором — по четырем. Во втором случае получен более простой результат. Результаты эквивалентны. Проверку можно выполнить, составив таблицу истинности.