Изучение подобия (традиционный и альтернативный подходы)

Вторым основным методом доказательства в геометрии после равенства является подобие, которое является центральным вопросом при изучении геометрических преобразований. Еще раз повторим, что оно рассматривается и как преобразование, и как отношение. Кроме того, изучение подобия связано с изучением тригонометрических функций. Если независимость отношения длин отрезков на стороне угла к длинам их проекций на другую сторону доказывается без использования подобия, то тригонометрические функции острого угла прямоугольного треугольника появляются раньше подобия и их можно использовать для доказательства признаков подобия или, наоборот, подобие используется в тригонометрии. Кратко обозначим основные особенности изложения вопроса о подобии в ныне действующих учебниках и методические рекомендации к изучению темы.

Учебник А. В. Погорелова:

• • подобие — преобразование фигур;
• • конструктивно определяется гомотетия, являющаяся преобразованием подобия и способом получения подобных фигур;
• • признаки подобия доказываются с помощью гомотетии;
• • к данной теме в учебнике приведен хороший набор задач, содержащих ряд новых теоретических фактов.

Возможная методика изучения.

Тщательно разобрать и уточнить доказательство первого признака подобия, составить план доказательства, второй и третий признаки предложить ученикам для самостоятельного изучения по составленному плану.

Подобие прямоугольных треугольников — для самостоятельного изучения с последующей проверкой.

Задачи разбить на несколько блоков, сходных по сюжетам. Там, где это целесообразно, организовать работу по поиску решения задачи, поскольку появился новый метод доказательства — метод подобия.

Рассмотрим пример организации поиска решения (доказательства) при работе со следующим заданием, которое может быть использовано не только при работе по учебнику А. В. Погорелова. Это задача о свойстве высоты, опущенной на гипотенузу треугольника.

Задание 18.1.

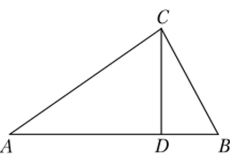
Па рис. 18.1 в прямоугольном треугольнике АВС (АС = 90°) проведена высота CD. Сколько прямоугольных треугольников на рисунке? Укажите подобные треугольники. Какие выводы о связи высоты CD с катетами треугольника и их проекциями на гипотенузу вы можете получить, используя подобие?

Рис. 18.1 Это _{один из} вариантов текста задания. Его можно упростить (конкретизировать) или усложнить. Приведем другие варианты текста задания.

• • На рис. 18.1 в прямоугольном треугольнике ЛВС (АС = 90°) проведена высота CD. Какие следствия вы можете получить?
• • На рис. 18.1 в прямоугольном треугольнике ЛВС (АС = 90°) проведена высота CD. Сколько прямоугольных треугольников на рисунке? Есть ли среди них подобные? Какие следствия из этого условия могут быть получены?

• На рис. 18.1 в прямоугольном треугольнике ЛВС (/.С = 90°) проведена высота CD. Сколько прямоугольных треугольников на рисунке? Найдите среди них подобные. Докажите, что CD² = ADBD. Какие еще соотношения можно получить из факта подобия треугольников?

Учитель может составить и другие варианты заданий. Естественно, опираясь на полученные результаты, предложить ученикам составить новое доказательство теоремы Пифагора. Учитель в этом случае может предложить его в виде задания «с пропусками».

Учебник Л. С. Атанасяна:

• • вводятся пропорциональные отрезки, подобные фигуры на житейской основе, дается аккуратное определение подобных треугольников, формулируется и доказывается лемма об отношении площадей подобных треугольников, на этой основе выполняется доказательство первого, на основе первого — второго признака, третьего через второй;
• • преобладают задачи на вычисление на непосредственное применение признаков подобия, несколько задач на построение;
• • в качестве одного из приложений подобия к решению задач рассматривается теорема о средней линии треугольника.

Возможная методика изучения:

• • лемму об отношении площадей можно оставить без доказательства;
• • хорошо отработать понятие «сходственные стороны» на готовых чертежах, как и применение признаков подобия, вычисление пропорциональных сторон;
• • теорема о средней линии — очень поздно, рассмотреть ее в этой теме с позиций еще одного способа доказательства известного факта;
• • обратить внимание на ряд задач (задача об отношении периметров подобных треугольников, задача о том, что отношение сходственных сторон равно отношению высот, теорема о пропорциональных отрезках, представленная как задача, и серия задач к ней, в частности на деление отрезка в данном отношении, задачи на построение методом подобия, задача об отрезке, соединяющем середины диагоналей трапеции, задача о свойстве биссектрисы угла треугольника). Последнюю задачу следует рассмотреть позже как еще один пример поиска решения задачи, а также пример обобщения результата на биссектрису внешнего угла треугольника. Ситуация самостоятельного поиска решения может быть организована с помощью задачи-шутки кота Сэмюэля. В ней описывается поиск решения задачи неким учеником и его размышления об обобщении полученного результата. Текст этой задачи целесообразно предложить школьникам для самостоятельного чтения и выполнения предложенных в тексте заданий. Также возможен вариант, когда эти рассуждения, опуская игровой момент, полностью приведет сам учитель. Понятно, что для успешного обучения самостоятельной деятельности по поиску решения геометрических задач ученикам следует приводить примеры такого поиска на хороших задачах.

Задача кота Сэмюэля

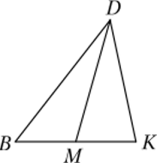
М.

Рис. 18.2

Один ученик захотел повысить свою итоговую отметку по теме «Подобие» и решил найти различные способы решения следующей задачи: доказать, что биссектриса угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Сделав рисунок (рис. 18.2) и составив требуемое.

ВЫ мк

равенство он начал рассуждать так: чтобы доказать это равенство, нужно выделить теоремы, в формулировках которых участвуют частное или произведение отрезков. Взяв несколько листочков для черновика, ученик последовательно написал на них:

теорема Фалеса, теорема синусов, площадь треугольника S = ~аЪ sin у, подобие — и начал заполнять каждый из листочков.

С «Фалесом» он справился быстро. Посмотрите на рис. 18.2 и предложите построения, которые позволят получить конструкцию из теоремы Фалеса. Какие случаи здесь возможны?

Какие треугольники, их стороны и углы следует задействовать, чтобы для доказательства нашего равенства можно было воспользоваться теоремой синусов?

Третий случай оказался сложнее. Чтобы получить требуемое соотношение — сказал себе ученик — мне нужно в формулы площади включить отрезки ВМ и ВО, МК и КО. Конечно, можно сразу включить их в формулу S= -ab sin у, но мне ничего не известно об углах В и К. Но, с другой стороны, у меня есть равные углы BDM и MDK

и можно записать формулы площади S_ABDSi = -BD DM sin ABDM,

1 ^.

S_AMDK= -DM• DKsin /LMDK. Правда, в равенствах появился лишний отрезок ОМ. Избавиться от него можно делением одного равенства на другое. Но как теперь задействовать отрезки ВМ и МК? Попробую выбрать формулу S = от лишнего элемента снова можно избавиться делением. Это доказательство готово.

Записав полученное обоснование, ученик приступил к поиску доказательства с использованием подобия. Если на рисунке нет подобных треугольников — подумал он — то нужно их построить. Самым простым в этом случае является построение треугольников с двумя равными углами, а равенство углов возникает при параллельных прямых и секущей. Значит, нужно провести прямую, параллельную, например, BD через точку К до пересечения с продолжением DM (см. рис. 18.2). Тогда треугольники BDM и МКС будут подобны (почему?), а дальше все получится автоматически.

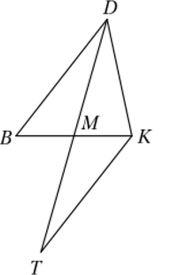
В этот момент зазвонил телефон и, пока ученик разговаривал со своим другом, его любимый кот Сэм играл с черновиками. Он порвал последний листочек, на котором чудом сохранился только чертеж, а листочки с первым и вторым доказательствами утащил и кудато спрятал.

Спасите кота от справедливого гнева ученика и помогите ему восстановить утраченные доказательства. Какое доказательство было записано учеником на сохранившемся листочке?

Вообще говоря, работа с данной задачей вовсе не заканчивается восстановлением доказательств, поскольку можно сформулировать обратное утверждение. Сделайте эго. Попробуйте обосновать его истинность. Какое утверждение вы для этого используете? Запишите результат.

Работа ученика не закончились оформлением решения задачи. Записав результат, он подумал, корректно ли сформулирована задача и нс может ли в ней идти речь о внешнем угле треугольника?

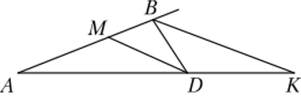
Рис. 183.

Тогда он нарисовал новую картинку — треугольник ABD, биссектрису внешнего угла ВК и решил попробовать построить отрезок DM, параллельный биссектрисе ВК, чтобы можно было вновь попытаться использовать обобщенную теорему Фалеса (см. рис. 18.3). Затем он выписал все возможные, по его мнению, отношения и начат их изучать.

AM ' AD

Объясните, каким образом получились такие отношения: — = —, ^{F J} ВМ KD

АВ АК DM «_м

= —. Проведя действия с первой пропорцией, он получил.

АВ ^лк «_П1#т/. _w

новую = —, в которой его не устраивал отрезок ВМ. Какой из сторон треугольника будет равен этот отрезок? Почему? Какие действия произвел ученик над пропорцией? Сформулируйте полученное им свойство биссектрисы внешнего угла треугольника в виде теоремы. Интересно, а будет ли в этом случае истинно обратное утверждение? Найдите ответ на этот вопрос.

Как видите, ученик нс только успешно справился со своей задачей, по и существенно расширил ее рамки, даже кот, названный, кстати, в честь Марка Твена (интересно, а почему Сэм?), не помешал ему в этом деле.

Кроме того, в качестве заданий для индивидуальной исследовательской работы ученикам следует предложить сформулировать и обосновать иные признаки подобия (как в свое время и иные признаки равенства), признаки подобия для равнобедренных и равносторонних треугольников, для прямоугольных треугольников. Также для самостоятельной работы целесообразно предложить микроисследование о виде четырехугольника и его площади (в учебнике Л. С. Атанасяна в задаче 568 — частный случай). Таким же образом следует организовать работу и с теоремой о среднем геометрическом, о пропорциональных отрезках в круге (примеры поиска доказательства с использованием нового метода — метода подобия).

Учебник И. М. и В. А. Смирновых:

• • определяются подобные треугольники (подобие выступает здесь как отношение);
• • имеет место единый подход к доказательству признаков подобия. Первый признак доказывается на основании теоремы о пропорциональных отрезках. Второй и третий признаки обосновываются с помощью дополнительного построения, аналогичного построению при доказательстве первого признака;
• • обучение применению признаков проходит на различных задачах, среди которых достаточно много заданий по готовым чертежам и задач на вычисление, что позволяет продолжить обучение школьников поиску решения задач;
• • дач ее рассматривается подобие как преобразование плоскости, приводятся его свойства, вводится гомотетия и устанавливается связь подобия и гомотетии;
• • теорема Пифагора доказывается на основе подобия треугольников;
• • тригонометрические соотношения в треугольнике вводятся после изучения подобия.

Возможная методика изучения;

• • актуализируется теорема о пропорциональных отрезках, вводится определение подобных треугольников;
• • доказательство первого признака подобия проводится под руководством учителя. При этом чрезвычайно важно обосновать выбор дополнительного построения — проведение параллельного отрезка. Поскольку для доказательства подобия мы можем воспользоваться только определением, то нам следует найти равные углы и получить пропорциональные стороны треугольников. Равенство углов и пропорциональность сторон возникают при параллельных отрезках и их секущих;
• • доказательство второго и третьего признаков при выполнении предыдущей рекомендации можно предложить для самостоятельной работы. Учитель ставит ученикам вопрос: что получится, если в условиях второго и третьего признаков мы применим построение, аналогичное построению при доказательстве первого признака?
• • закрепление признаков проводится на заданиях по готовым чертежам. При работе с задачами на вычисление и доказательство следует продолжить работу по обучению учеников поиску решения задач с помощью восходящего анализа, нисходящего анализа;
• • материал учебника о «золотом сечении» следует предложить для самостоятельного чтения перед его изучением, а на уроке заслушать развернутые сообщения учеников по теме, которые с помощью учителя они заранее подготовят;
• • доказательство теоремы Пифагора, оформленное в виде задания с пропусками (пример доказательства для учебника Л. С. Атанасяна приведен ниже) можно предложить для самостоятельной работы.

В данном параграфе мы не приводим анализ содержания темы «Подобие» в учебнике А. Д. Александрова, поскольку в логике данного учебника мы покажем иной подход к изучению темы, в основе которого лежит самостоятельная познавательная деятельность школьника, организуемая с помощью специально составленных заданий.

Как известно, введение в курсе геометрии тригонометрических соотношений в прямоугольном треугольнике связано с обоснованием независимости отношения длины наклонной к длине ее проекции от выбора точки на стороне угла. Эта проблема может быть решена средствами подобия, тогда тригонометрические соотношения в треугольнике вводятся в теме «Подобие» (учебник Л. С. Атанасяна) либо с помощью площади треугольника (учебник А. Д. Александрова), а тригонометрические соотношения могут быть введены при изучении теоремы Пифагора, что существенным образом расширит тематику задач и позволит доказать теоремы синусов и косинусов, которые в дальнейшем могут быть применены для доказательства признаков подобия треугольников. Рассмотрим этот вариант построения учебного материала.

Попутно заметим, что само доказательство теоремы Пифагора может быть представлено в виде задания с пропусками для организации самостоятельной работы учеников.

Задание 18.2

На рис. 18.4 выполнены следующие построения: на сторонах квадрата ABCD взяты точки К, L, М> N следующим образом: КВ = LC = MD = = AN = aBL = LM = DN = AK = b.

Определите вид четырехугольника KLMN на рис. 18.4.

По данным на рисунке определите площадь исходного квадрата и треугольников. Используя эти результаты, заполните пропуски в следующих формулах.

Рис-18.4 тогда с² = … + …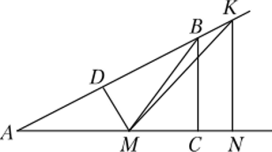

Какую связь между сторонами прямоугольного треугольника вы смогли установить, заполняя пропуски в равенствах?

Эта связь выражает одну из самых известных теорем геометрии — теорему Пифагора. Сформулируйте ее. Из каких этапов состоит доказательство теоремы. На каких фактах оно основано?

Что вам известно о Пифагоре, о доказательствах теоремы? Подготовьте рассказ о том, что такое «пифагоровы треугольники», какой треугольник называется «египетским» и почему, для чего использовали этот треугольник?

Для введения тригонометрических соотношений в треугольнике можно предложить два задания.

Задание 18.3

Как вы можете определить высоту дерева? Какие способы для этого вы могли бы предложить?

Как вы поступите, если дерево окажется в недоступном для вас месте?

Какие измерения и построения на местности вы уже умеете выполнять? А о каких измерениях на местности и приборах для этих целей вы знаете?

Составьте рассказ исторического или приключенческого жанра об измерениях на местности.

Задание 18.4

Из истории вы знаете, что первым массовым учебником математики в России была «Арифметика» Л. Ф. Магницкого, написанная для учеников Школы математических и навигацких наук. Специалисты по навигации должны были знать элементы тригонометрии, чему и был посвящен один из разделов «Арифметики». В нем, в частности, определялись тригонометрические функции острого угла прямоугольного треугольника: синус, косинус, тангенс, котангенс. Найдите в справочниках по математике определения этих понятий. Какие еще тригонометрические отношения вы нашли в справочниках?

Знаете ли вы что-либо из истории Школы математических и навигацких наук?

Чем, но вашему мнению, занимается тригонометрия? Что вы знаете об истории тригонометрии?

В результате выполнения этих заданий школьники формулируют определение синуса, косинуса, тангенса, котангенса острого угла прямоугольного треугольника, устанавливают связь между сторонами и углами. Далее ставится проблема равенств соответствующих отношений для равных углов. Если предварительно этот вопрос был рассмотрен в лабораторной работе, которая выполнялась еще при изучении простейших геометрических построений с помощью циркуля и линейки, тогда для обоснования этой независимости можно предложить задание 18.5 в следующей формулировке.

Задание 18.5.

Исследуя в лабораторной работе отношение катета к гипотенузе и отношение катетов прямоугольных треугольников с общим острым углом, вы установили, что это отношение не зависит от выбора точки на стороне угла. Для обоснования данного вывода выполните следующие задания, используя рис. 18.5.

Рис. 18.5

Выразите площади треугольников АМВ, АМК, используя в качестве высот МД ВС, KN. Следует ли из этих формул равенство Можно ли на основе данного отношения доказать утверждение: синус угла зависит только от величины данного угла ?

Далее самостоятельно вывести теоремы синусов и косинусов поможет ученикам выполнение следующих заданий.

Задание 18.6.

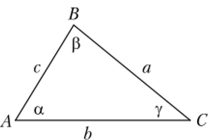
Рис. 18.6

По данным на рис. 18.6 выразите высоту CD треугольника АВС. Докажите истинность.

sin a sin В равенства-= —-—.

а о

Будет ли это равенство выполняться в прямоугольном, тупоугольном треугольнике? Почему?

Как теперь вы можете обосновать, что в любом треугольнике будет si и Л sin В sin С _л

истинным равенство-= —-— =-. Оно выражает теорему си;

а о с

нусов. Сформулируйте эту теорему. Изменится ли доказательство, если один из углов — А или В — будет тупым?

Вспомните признаки равнобедренного треугольника. Можете ли вы с помощью теоремы синусов обосновать какой-либо из признаков? На каком основании вы выбрали данный признак?

Задание 18.7.

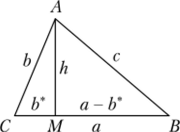
Кроме теоремы синусов существует еще и теорема косинусов, которая формулируется следующим образом: «Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними». В обозначениях рис. 18.7 запишите соответствующее вы- Рис. 18.7 ражение для каждой из сторон треугольника.

Будет ли это утверждение верным, если Z.С = 90°?

Задание 18.8.

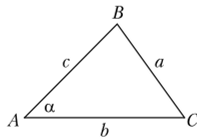
М а Рис. 18.8.

Пользуясь обозначениями на рис. 18.8, заполните пропуски в доказательстве теоремы косинусов.

Из треугольника САМ Ь* = … cos С.

Но теореме Пифагора из треугольника МАВ с²= Л²+ …

По теореме Пифагора из треугольника MAC

h²=b²-…

Тогда с² = И'² + … = Ь² — … = а¹ + Ь² — 2? а? b ? cos С.

Что изменится в доказательстве теоремы, если треугольник АСВ будет тупоугольным (угол С — тупой)?

С помощью теоремы косинусов выразите диагонали параллелограмма через его стороны. Какой будет связь между сторонами и диагоналями параллелограмма?

Раннее введение тригонометрических функций острого угла позволяет расширить запас формул площадей треугольника и частных видов четырехугольников, а также ввести формулу Герона. Вывод формулы Герона также можно представить в форме рассказа ученика о его поиске решения (задание 18.9).

Задание 18.9.

Один восьмиклассник нашел в справочнике формулу Герона и рассказал на уроке, как она выводится. 11а перемене на доске он подготовил чертеж (рис. 18.9) и сделал ряд записей с пропусками, которые заполнял в ходе своего рассказа. Прочтите рассказ ученика и заполните пропуски в сделанных им записях.

«Нам известны две формулы площади треугольника: S = -Acsin… и S = -bh,. Чтобы полу-.

2 2 ^ь 9 Рис. 18.9

чить формулу Герона нам нужно из первой формулы исключить sin а, а из второй высоту треугольника, заменив их другими его сторонами. Рассмотрим первый случай. Стороны треугольника участвуют в формуле теоремы косинусов. Для угла эта формула примет вид а² = Ь² + с² + 26с cos а.

Выразив отсюда cos а, получаем cos, а =-. Чтобы заменить в фор-

2 Ьс

муле площади синус косинусом, воспользуемся тригонометрической единицей:

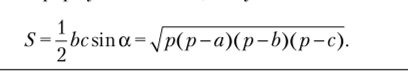
Заменив в этой формуле сумму сторон удвоенным полу периметром,.

2 __.

получаем sina = — Jр (р-а)…(р-с)".

Ьс

Возвращаясь к формуле площади, получим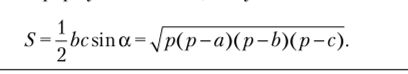

Далее мы рассмотрим возможный вариант изучения подобия. В основу этих рекомендаций будет положена организация самостоятельной деятельности школьников, а также знание ими тригонометрии.

Мобилизовать учеников на изучение понятийного аппарата темы поможет следующее задание.

Задание 18.10.

В четырнадцатой главе первой части своего романа «Таинственный остров» Жюль Верн рассказывает, как один из главных героев Сайрес Смит измеряет высоту плато Кругозора над уровнем моря, точнее говоря, вычисляет эту высоту, используя подобие треугольников. Внимательно прочтите указанный выше фрагмент романа. Установите, какой была процедура вычислений, какие измерения были проведены, какими теоретическими фактами воспользовался инженер Смит для вычислений. Сделайте соответствующий описанной в романе ситуации рисунок.

Как по-иному можно было вычислить высоту скалы? Какие измерения и вычисления следовало для этого провести? Какие инструменты для этого вам бы понадобились?

Какие треугольники называются подобными, какие признаки подобия треугольников существуют? Что называется коэффициентом подобия?

Где вы встречались с подобными фигурами? Какие фигуры называются подобными? Нарисуйте подобные фигуры.

Провести самостоятельный поиск доказательства признаков подобия треугольников с помощью теорем синусов и косинусов помогут следующие задания.

Задание 18.11.

Самым простым признаком подобия треугольников является следующий: «Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны».

Что в соответствии с определением подобных треугольников нужно проверить при доказательстве этого признака?

Вспомните те теоремы, в которых говорится о пропорциональности отрезков. Можете ли вы привести доказательство данного признака, используя, например, теорему синусов? Какие еще теоретические факты вам потребовались при доказательстве теоремы?

Задание 18.12.

В любом справочнике по геометрии, кроме сформулированного в задании 18.9 признака подобия треугольников, вы обязательно отыщете еще два: «Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то треугольники подобны», «Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то треугольники подобны». В нервом случае для обоснования признака нужно либо подводить эти треугольники под соответствующее определение, либо воспользоваться первым признаком подобия треугольников. С помощью какой теоремы вы можете провести обоснование сформулированного признака? Сумели ли вы найти в справочниках или учебниках еще какие-либо доказательства данного признака?

Проведите аналогичную работу с третьим признаком подобия.

Как и при традиционном подходе к изучению подобия, мы рекомендуем закрепление признаков подобия выполнять на готовых чертежах. Большое количество таких заданий представлено в учебниках А. Д. Александрова.