Основные показатели динамики

Для количественной оценки динамики социально-правовых явлений применяются такие статистические показатели, как абсолютные приросты, темпы роста, темпы прироста, которые делятся: на базисные, цепные и средние. В основе расчета этих показателей динамики лежит сравнение уровней ряда динамики. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления (например, число осужденных по статьям УК РФ с 1997 г. — года вступления его в силу). Если сравнение осуществляется при переменной базе и каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные таким образом показатели динамики называются цепными.

Для рядов динамики со значительными колебаниями уровней в качестве базы сравнения применяются средние уровни.

Абсолютный прирост (Ду) равен разности двух сравниваемых уровней ряда.

Базисный абсолютный прирост Д= y_t— У (_у

Цепной абсолютный прирост Дy_t = y_t — y_t__{.

iy _ 'll

Средний абсолютный прирост Ay = ———,.

п-1.

где y_t — уровень сравниваемого периода; y_t__x — уровень предшествующего периода; у§ — уровень базисного периода; у_ь у_п — первый и последний уровни ряда соответственно; п — число уровней ряда.

Темп роста (Г) — отношение уровня ряда одного периода к уровню ряда другого периода, выраженное в процентах.

Базисный темп роста Г/' = — • 100.

Ус,

у

Цепной темп роста Т_г= —-100.

Ум.

Средний темп роста Т — «-ч— • 100.

У

Замечание. Если темп роста и средний темп роста вычисляются в долях (нс умножаются на 100), то они называются соответственно коэффициентом роста и средним коэффициентом роста.

Темп прироста (Г_пр) — отношение абсолютного прироста (Ду) к уровню, принятому за базу сравнения, выраженное в процентах.

Темп прироста показывает, на сколько процентов изменился сравниваемый уровень, но отношению к уровню, принятому за базу сравнения. Он может быть положительным, отрицательным или равным нулю.

Базисный темп прироста 7'fi, _t = —— • 100.

Ус,

Цепной темп прироста Т_{, = —• 100.

Ум.

Средний темп прироста Т_Щ) = Т -100.

Замечание. Если вычислен соответствующий темп роста, то темп прироста равен:

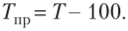
Сведем выражения для вычисления указанных выше показателей динамики в табл. 6.6.

Таблица 6.6

Формулы для вычисления показателей динамики.

Пример. Рассчитать базисные (приняв за базисный период январь), цепные и средние абсолютные приросты, темпы роста и темпы прироста числа зарегистрированных в городе преступлений, используя данные за период с января по май из табл. 6.7.

Решение. Используя формулы, приведенные в табл. 6.6, рассчитаем базисный абсолютный прирост, цепной абсолютный прирост, базисный темп роста, цепной темп роста (табл. 6.7), базисный темп прироста, цепной темп прироста (табл. 6.8).

Расчеты показателей динамики.

Таблица 6.8

Расчеты базисного и цепного темпов прироста.

". _,. _Л_ у₅~У1 325−332.

Средний абсолютный прирост Ау = ^4—— =-= -1,75.

5−1 4.

Средний темп роста Т = -100 = 100 = 99,5 (%).

У V 332.

Средний темп прироста Т_т =7'-100 = 99,5−100 = -0,5 (%).

Наряду с указанными показателями в ряд}' динамики может быть рассчитан средний уровень ряда. Он применим для любого ряда динамики: интервального и моментного.

В интервальных рядах динамики средний уровень ряда (у) определяется делением суммы уровней ряда на их число, т. е. по методу средней арифметической:

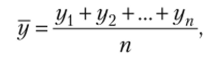
где у_{, у₂>у_п — значения уровней ряда; п — число уровней.

Пример. Рассчитать средний уровень ряда, используя данные о количестве зарегистрированных преступлений из табл. 6.7.

Решение. Поскольку представленный в табл. 6.7 ряд является интервальным, то применим приведенную выше формулу для среднего уровня ряда:

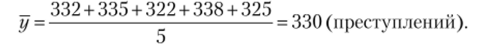
В моментныхрядах для вычисления среднего уровня ряда применяется средняя хронологическая — средняя, вычисленная по значениям, изменяющимся во времени.

В моментном ряду с равными интервалами времени средний уровень — средняя хронологическая моментного ряда — определяется по формуле.

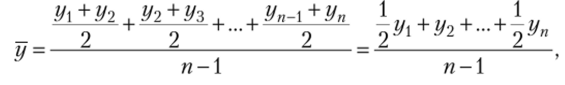
где у_{, у₂уу" — значения уровней ряда; п — число уровней.

Пример. Имеются следующие сведения на первое число соответствующего месяца об уголовных делах, не законченных следственным отделом в срок, установленный УПК РФ:

Дата… 01.01.2014 01.02.2014 01.03.2014 01.04.2014 01.05.2014 01.06.2014.

Число уголовных дел… 18 24 17 28 22 32.

Найти среднемесячное количество уголовных дел, не оконченных в данном следственном отделе в срок, установленный УПК РФ.

Решение. Поскольку имеющиеся сведения представляют собой моментный ряд с равными интервалами, то среднемесячное количество незаконченных уголовных дел рассчитывается следующим образом:

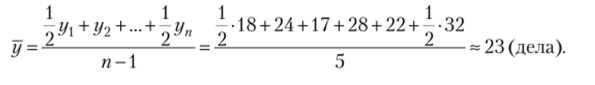
В моментном ряду с неравными интервалами времени средний уровень ряда определяется, но формуле средней хронологической взвешенной:

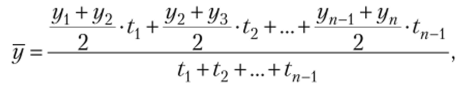
где у_ь у₂, у_п — значения уровней ряда; п — число уровней; ?_1? t₂,…, t_n__x — длительность интервалов времени между уровнями.

Пример. Имеются сведения о количестве выявленных в субъекте РФ нарушениях земельного законодательства юридическими лицами по состоянию на определенные даты:

Дата… 01.01.2004 01.01.2006 01.01.2010 01.01.2011 01.01.2014.

Количество нарушений… 112 137 103 142 124.

Требуется определить среднегодовое количество выявленных в субъекте РФ нарушений земельного законодательства юридическими лицами за период с 01.01.2004 по 01.01.2014.

Решение. Поскольку имеющиеся сведения представляют собой моментный ряд с неравными интервалами, то для расчета искомого значения воспользуемся формулой средней хронологической взвешенной.

Из условия задачи следует: у_х = 112, t_{ = 2 (года); у₂ = 137, t₂ = 4 (года); у₃ = 103, t₃ = 1 (год); у_л = 124, t₄ = 3 (года).

Подставив указанные значения в соответствующую формулу, получим:

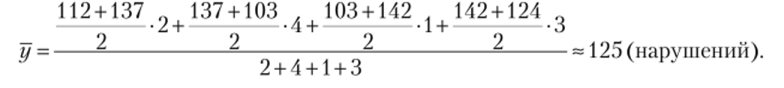
Расчет среднего абсолютного прироста или среднего темпа прироста может быть произведен по двум значениям — по первому и последнему уровням ряда.

Подсчитав количество рядов, в формулу вводится значение на одну единицу меньше: разность значений последнего и первого уровней ряда, деленное на число рядов, уменьшенное на единицу.

При расчете среднего темпа прироста в MS Excel следует использовать функцию «Степень»^[1] (рис. 6.2). Среднее значение темпа роста будет вычисляться по формуле: частное последнего и первого уровней ряда в степени, обратной числу уровней ряда за минусом единицы — 1 /(п — 1). Средний же темп прироста вычисляется по формуле Т_ир =Г-100.

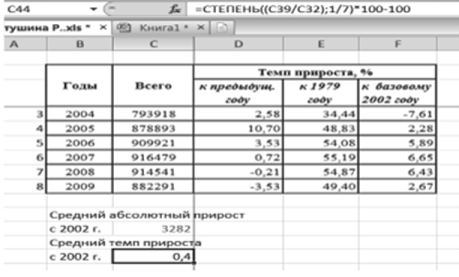
Рис. 6.2. Расчет среднего темпа прироста

Т будет рассчитываться как средняя геометрическая уровней ряда. Формула средней геометрической.

где х — значение уровня ряда; N — число значений уровней ряда.

• [1] Степень — это обратная величина от корня.