Уравнение Шрёдингера для бесспиновой частицы в магнитном поле

Ясно, что магнитное ноле должно влиять на электрон в атоме водорода, причем такое влияние будет, даже если отвлечься от наличия у электрона спина. Ниже и произведен учет влияния магнитного поля на электрон в атоме водорода в приближении нулевого спина у электрона (называемого в таком случае бсссннновым).

Итак, выясним, как влияет магнитное иоле на уровни энергии одноэлектронной бесспиновой системы, описываемой уравнением Шрёдингера, для чего рассмотрим гамильтониан бесспиновой частицы Н^т при наложении на систему магнитного поля.

Из механики известно, что функция Гамильтона заряженной частицы, находящейся в магнитном поле, имеет вид.

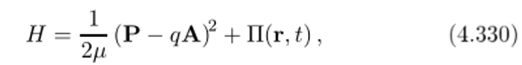
где // и q — масса и заряд частицы, Р — так называемый обобщенный импульс частицы, П (г, t) — потенциальная энергия частицы в потенциальном поле (каковым является, как известно, электрическое поле), А — векторный потенциал поля, ротор которого равен индукции магнитного поля:

Для статического однородного магнитного ноля (направляя вдоль которого ось 2, получим В = B_zк), в качестве векторного потенциала можно выбрать функцию.

где i, j, k — орты декартовой системы координат^177 178.

Не останавливаясь на обосновании того, что обобщенному импульсу в квантовой механике соответствует тот же оператор, что и обыкновенному импульсу, сопоставим по обычному правилу функции Гамильтона (4.330) гамильтониан.

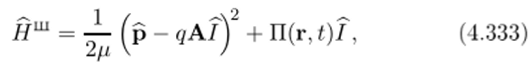
где р — оператор импульса, компоненты которого определяются соотношениями (4.124).

Возведение в квадрат члена в скобках в правой части (4.333) должно дать самосопряженный оператор. Так как векторный потенциал является функцией декартовых координат, он, вообще говоря, не коммутирует с оператором импульса, однако решение задачи 4.6 позволяет понять¹'⁸, что самосопряженным должен быть оператор

^[1][2]

В гамильтониане (4.334) для бесспиновой заряженной частицы, учитывающем действие однородного статического магнитного ноля, появились два новых члена: один — линейный по векторному потенциалу, а другой — квадратичный.

Убедимся, что в статических магнитных нолях квадратичный, но векторному потенциалу член дает пренебрежимо малый вклад в энергию состояния. Для этого воспользуемся оценкой векторного потенциала А ~ В-ai, которая следует из (4.332), если в это выражение вместо координат подставить величину боровского радиуса сц = 0.53−10″¹⁰ м как характерную область, в которой сосредоточена плотность вероятности обнаружения электрона в атоме водорода. Тогда не представляет труда убедиться, что при B_z = 1 Тл величина е²Bdj (2т_е) ~ Ю"¹⁰ эВ. Столь малой величиной (на 11 порядков меньшей абсолютного значения энергии основного состояния атома водорода) можно пренебречь по сравнению с гораздо большими эффектами, о которых пойдет речь ниже. Далее квадратичный по магнитному нолю член в (4.334) учитывать не будем.

Раскрыв действие оператора рА + Ар на волновую функцию ?ф (г) с учетом явного вида оператора импульса р и явного вида (4.332) векторного потенциала, получим:

где было использовано определение (4.194) оператора Ь₂. Последнее соотношение показывает, что ранее был выбран именно самосопряженный оператор рА + Ар, который с точностью до вещественного множителя оказался просто оператором декартовой проекции орбитального момента импульса.

Таким образом, гамильтониан бесспиновой частицы в постоянном магнитном поле принимает окончательный вид.

Два первых слагаемых в гамильтониане (4.335) описывают одноэлектронную систему в отсутствие магнитного поля, а последний член отвечает наложению на систему постоянного магнитного поля, направленного вдоль оси г, индукция которого имеет величину B_z.

Энергия водородоподобного иона в постоянном магнитном поле в бесспиновом приближении Определение вида гамильтониана, описывающего одноэлектронную бесспиновую систему в магнитном поле, позволяет решить вопрос о влиянии постоянного внешнего магнитного поля на уровни энергии водородоподобного иона. Помещение последнего в однородное статическое магнитное поле добавляет к гамильтониану (4.246) дополнительный член из (4.335), в результате имеем.

где H_fl — гамильтониан (4.246) водородоподобного иона в отсутствие внешнего магнитного поля, и было учтено, что заряд электрона q = — е.

В разд. 4.6 было показано, что гамильтониан водородонодобного иона в отсутствие магнитного поля взаимно коммутативен как с оператором квадрата момента импульса L², так и с оператором проекции момента импульса Ь_г. Так как последние два оператора взаимно коммутативны, а сам с собой коммутирует любой оператор, то очевидно, что и гамильтониан (4.336) взаимно коммутативен с операторами L² и L_z. Поэтому гамильтониан.

(4.336) должен иметь общие собственные функции с операторами.

L² и L., как это имело место и для гамильтониана водородоподобного иона (4.246) в отсутствие магнитного ноля.

Таким образом, задача квантования гамильтониана (4.336) сводится к подстановке общих собственных функций операторов.

^л г) *^/-v

L" и L_z в уравнение на собственные значения.

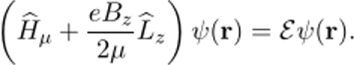
Подстановка одной из общих собственных функций операторов квадрата момента импульса и^{-проекции} орбитального момента импульса¹'⁹ ф = Я (г)У/_тД^, ip), а также учет действия на последнюю оператора L_z (L_zip = пцНф) показывают, что уравнение на собственные значения гамильтониана водородоподобного нона в постоянном магнитном поле сводится к задаче на собственные значения гамильтониана водородоподобного иона без ^179[3]

магнитного поля, но с видоизмененной энергией:

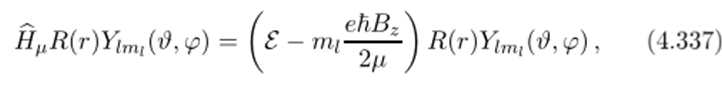
где гщ — магнитное квантовое число.

Квантование водородоподобного иона с «бесспииовым» электроном было выполнено в разд. 4. G, откуда в качестве решения задачи на собственные значения гамильтониана (4.337) получаем: в магнитном поле вырождение по магнитному квантовому числу уровней энергии водородоподобного иона с «бесспиновым» электроном снимается, и уровни расщепляются на 21 4- 1 подуровень, энергия которых определяется выражением.

где квазистациоиарные уровни энергии водородоподобиого иона определяются выражением (4.258), и было использовано определение магнетона Бора (4.319).

Итак, в бесспиновом приближении оказывается, что внешнее постоянное магнитное поле не влияет на уровни энергии водородоподобного иона в s-состояниях, поскольку в последних I = О и пц = 0.

С учетом же спина электрона окажется (см. следующий подразд.4.7.2), что во внешнем постоянном магнитном поле уровни энергии s-состояний водородоподобного иона ]ю, сщепляются на два подуровня, отстоящие от уровня энергии состояния в отсутствие магнитного ноля на величину В частности, при.

B_z = 1 Тл изменение энергии 6-уровня водородоподобиого иона HbB_z = 0.575 • 10″⁴ эВ, что на б порядков превышает эффект, даваемый ранее отброшенным квадратичным членом, и может быть зафиксировано спектроскопическими методами.

• [1] Проверьте, что векторный потенциал (4.332) действительно соответствует постоянному магнитному полю с единственной компонентой вдоль оси z.
• [2] Далее самосопряженность полученного оператора станет очевидной.
• [3] См. стр. 222.