Математические модели ректификационных колонн при разделении многокомпонентных смесей

Описание математических моделей узлов ректификации многокомпонентных криогенных смесей затрудняется из-за недостаточной разработки вопросов массообмена, а порой и фазового равновесия этих систем. Рассмотрим наиболее распространенные модели.

Модель С

Описание модели основано на допущениях, принятых в модели А, с предположением, что унос жидкости постоянен и локальный коэффициент эффективности тарелки для всех компонентов имеет среднее значение. При отсутствии уноса модель представляет собой теоретическую ступень разделения.

Уравнения для j-го компонента разделяемой системы:

;

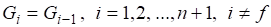
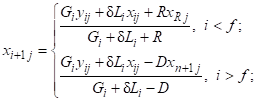
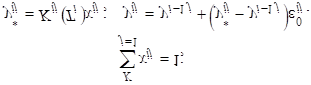
Уравнения описывают покомпонентный материальный баланс.

Уравнения расчета фазового равновесия выбираем в зависимости от свойств разделяемой двухфазной системы (см. разд. 1). Модель имеет один параметр настройки, и блок-схема расчета алгоритма модели близка по своей структуре к блок-схеме модели А.

Модель D

Одним из способов решения задачи распределения компонентов по высоте ректификационной колонны является метод независимого определения концентраций [38], согласно которому система потарелочных балансовых уравнений приводится к линейной или квазилинейной системе относительно xij путем замены.

.

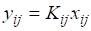
где Kij — константа фазового равновесия j-го компонента.

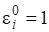
При этом рассматриваем теоретическую ступень разделения при постоянстве потоков пара Gi и жидкости Li.

Уравнения потарелочных материальных балансов по j-му компоненту имеют следующий вид:

для i-й тарелки (см. рис. 2, а).

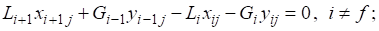
для тарелки питания (см. рис. 3, в) при i = f

.

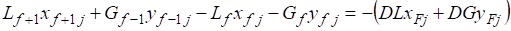
Уравнения материального баланса для конденсатора и испарителя в зависимости от режима работы соответствуют зависимостям (30), (31) и (33), (34).

С учетом зависимости (51) исходную систему уравнений преобразуем относительно определяемых концентраций и после определения коэффициентов.

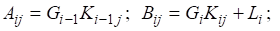
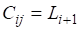
и правой части.

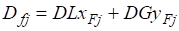
приводим к виду, удобному для решения на ЭВМ:

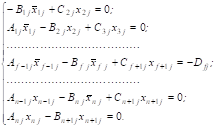
Систему уравнений вида (54) записываем для каждого компонента исходной смеси (j.= 1, 2, …,K); она представляет собой трехдиагональную матрицу коэффициентов Аij, Вij, Cij при переменных концентрациях.

Поскольку рассматриваемая задача является краевой, то систему уравнений (54) решаем с учетом граничных условий, которые определяются режимом работы конденсатора и куба, а в «открытых» колонных аппаратах — условиями ввода потоков питания и вывода продуктов разделения.

Систему уравнений (54) решаем методом прогонки [38], реализованным с помощью процедуры CODIA (рис. 10).

Для решения исходной нелинейной системы необходимо многократно повторять решение системы (54), каждый раз уточняя значения констант равновесия. Поскольку начальное приближение задано произвольно, полученное значение xij для каждого из компонентов не будет удовлетворять условию, когда сумма концентрации на каждой из тарелок будет равна единице или соответствовать заданной точности, т. е.

.

Следующим этапом является нормирование состава на каждой из тарелок по уравнению.

.

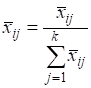
т. е. вычисление нового приближения для профиля концентраций и повторение расчетной процедуры, начиная с определения констант фазового равновесия. Число итераций, необходимых для получения конечного результата, зависит как от заданной точности е, так и от моделируемого режима разделения.

Критерием корректного решения рассматриваемой задачи является сходимость не только потарелочных материальных балансов, но и внешнего материального баланса колонны.

Сходимость решения при моделировании статистического процесса ректификации многокомпонентной смеси в простых колоннах может быть обеспечена также с помощью И-метода [см. уравнения (41)-(46)].

При проведении моделирования процесса ректификации в сложных колоннах и при наличии одного или нескольких боковых выводов продуктов разделения для обеспечения сходимости решения предлагается [39] более сложная реализация И-метода.

При условии, что в колонне (см. рис. 1, б) разделяется смесь, состоящая из распределяющихся компонентов, существует следующая взаимосвязь между откорректированными соотношениями массового потока j-го компонента и полученными на определенном этапе расчета:

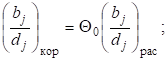
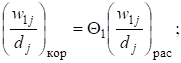
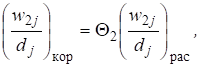
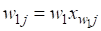
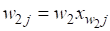
где — массовый поток j-го компонента в потоке w1; - массовый поток j-го компонента в потоке w2.

Откорректированный материальный баланс сложной колонны.

.

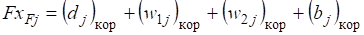
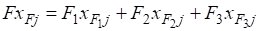
где — массовый поток j-го компонента в потоках питания.

В результате преобразования уравнения материального баланса (60) и его решения [с учетом соотношений (57)-(59)] относительно откорректированного массового потока j-го компонента в дистилляте получаем.

.

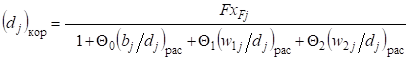
Условие сходимости по каждому потоку продуктов разделения определяем из равенств.

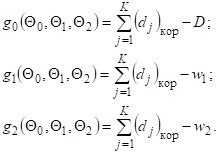
Искомое решение представляет собой положительные значения корректировочных коэффициентов И0, И1, И2, которые одновременно удовлетворяют условию равенства функций (62)-(64) нулю, т. е. g0 = g1 = g2 = 0.

Использование при решении уравнений (61)-(64) способа Ньютона-Рафсона приводит к наилучшим результатам, когда первое значение для каждого И? берется равным единице, т. е. .

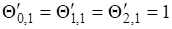
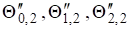
Расчет начинаем с определения функций (61)-(64) и их частных производных, исходя из первого принятого значения И?. Затем решаем уравнение Ньютона-Рафсона и получаем вторые приближения И?, а именно, которые используются для следующего приближения. Если при принятом значении И? получаются отрицательные значения в И??, то следует взять для следующего приближения в И? = И??/2.

Таким образом, зная значения корректировочных коэффициентов и количество j-го компонента, во всех выводимых потоках можно осуществить перерасчет концентраций в получаемых продуктах разделения.

В качестве независимых переменных заданы F, xF, бG, D, G1, f, n. Зная энергетическое состояние питания бG, определяем DL и DG и рассчитываем значение потока пара и жидкости по высоте колонны (блок 2). В блоке 3 задается предварительное значение вектора концентрации жидкости, обычно равное составу потока питания, и в блоке 4 рассчитываются значения констант фазового равновесия разделяемой смеси.

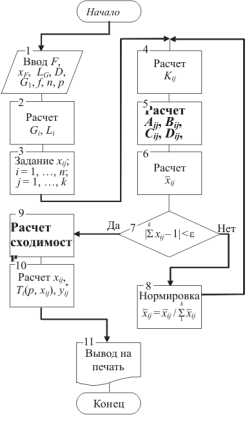
Рис. 10. Блок-схема алгоритма расчета модели D

Далее в блоке 5 производится расчет коэффициентов системы уравнений и определяется вектор концентрации (блок 6). В блоках 7, 8 осуществляется сопоставление потарелочного материального баланса (55), а в случае необходимости — его нормировка и передача информации в блок 4 вычисления нового приближения для профиля концентрации. В блоке 9 в зависимости от типа ректификационной колонны обеспечивается сходимость внешнего и внутреннего материального баланса. Затем исходные данные передаются в блок 10 для уточнения величины расчета температур и определения состава паровой фазы. Блок 11 обеспечивает печать и вывод результатов вычислений.