Потоки событий (Пуассоновские потоки)

Под потоком событий понимается последовательность однородных событий, следующих одно за другим в случайные моменты времени (например, поток запросов к серверу базы данных, поток покупателей в магазине, поток клиентов в парикмахерской и т. п.).

Поток называется ординарным, если события происходят поодиночке. Интервалы 7J, Т₂,…, Т_п ординарного потока могут быть одинаковыми или различными, дискретными или непрерывными, случайными или неслучайными (рис. 11.3).

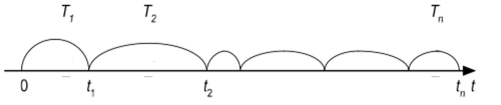
Рис. 11.3. Ординарный поток событий

Поток характеризуется интенсивностью Я — частотой появления событий или средним числом событий, поступающих в систему массового обслуживания (СМО) в единицу времени.

Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени. Примером такого потока может служить поток входящих (выходящих) почтовых сообщений на персональном компьютере (почтовая программа соединяется с сервером через каждые 10, 20, … минут).

Поток случайных событий называется пуассоновским, если число т событий потока, попадаемых на любой участок г оси времени, распределено по закону Пуассона.

где а — среднее число событий, приходящихся на участок времени г.

Пуассоновский поток является стационарным, если плотность потока событий Л = const, тогда среднее число событий а = Лт, и нестационарным, если X = X (t), тогда.

Рассмотрим случайную величину Т — интервал времени между соседними событиями в стационарном пуассоновском потоке — и определим ее функцию распределения: Р (т) = Р (Т < г). Выражение Т < г означает, что в интервале времени г наблюдается хотя бы одно событие потока. Выразим F® через F₀(t) — вероятность того, что в интервале времени г не наблюдается ни одного события потока:

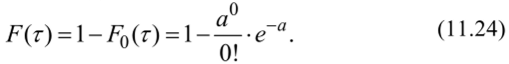
Таким образом, для стационарного пуассоновского потока функция распределения времени между соседними событиями и плотность распределения соответственно равны: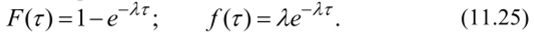

Из (11.25) следует, что интервал времени подчинен экспоненциальному (показательному) закону распределения, параметры которого равны: т_т = а_т = 1 / Я.

Если величины 7) являются зависимыми случайными величинами, то поток называется потоком с последействием, так как для любого момента времени последующее течение потока находится в вероятностной зависимости от предыдущего. Если СВ 7] независимы, то случайный поток называется потоком с ограниченным последействием и плотность вероятности системы можно представить в виде:

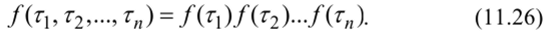
Таким образом, в случае стационарного пуассоновского потока все интервалы 7j, Г₂,…, 7), имеют одинаковые законы распределения f_i(r_i) = /(г,), где 1 = 1, 2,…, п, что является проявлением отсутствия последействия.

Случайный поток событий, который обладает свойством стационарности, ординарности и не имеет последействия, называется простейшим и является стационарным пуассоновским потоком.

ПРИМЕР 6. На кафедральный сервер поступает простейший ноток запросов с интенсивностью 2 = 0,3 запроса в минуту. Какова вероятность того, что за 5 минут: а) не придет пи одного запроса; Ь) придет ровно 5 запросов; с) придет хотя бы один запрос?

РЕШЕНИЕ. Случайная величина X — число запросов к кафедральному серверу за пять минут — распределена по закону Пуассона, параметр которого равен: а = Яг= 0,3 • 5 = 1,5.

a) Вероятность того, что за 5 минут не придет ни одного запроса (т = 0) вычислим по формуле (11.22): Р₀(5) = е¹'⁵ = 0,2231.

1 5⁵

b) Вероятность пяти запросов (т = 5): Р₅(5) == 0,1 412.

c) Вероятность хотя бы одного запроса:

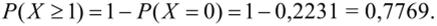
Для простейшего потока с интенсивностью Л вероятность попадания на элементарный (малый) отрезок времени At хотя бы одного события потока равна согласно (11.25):

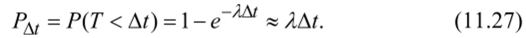
Данная формула получается при разложении экспоненты в ряд Тейлора по степеням At, причем ограничились только двумя первыми членами ряда. Понятно, что формула будет тем точнее, чем меньше At.