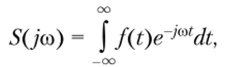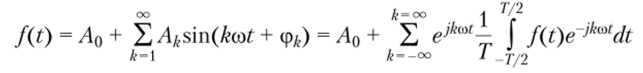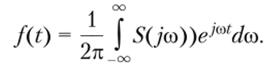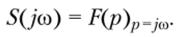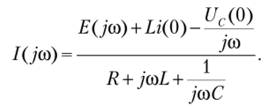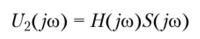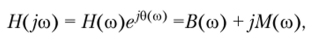Цепи при непериодических (импульсных) воздействиях

При анализе реакции цепи на воздействие импульсных сигналов, а также при расчете переходных процессов (аналогично операторному методу) применяется спектральный (частотный) метод.

Интеграл Фурье

Спектральный (частотный) метод дает возможность преобразовать функцию времени /(?) в функцию частоты S (jco), которую называют спектром функции f (t). Это преобразование выполняется с помощью интеграла Фурье (прямого преобразования Фурье).

который получают из формулы для ряда Фурье.

предельным переходом при стремлении Т к бесконечности. На функцию оо.

J /(?) накладывается ограничение — необходимо, чтобы она была конеч;

— оо на (не бесконечна). Ряд функций не удовлетворяет этому условию.

Для нахождения функций времени /(?) по известному спектру S (jco) используют обратное преобразование Фурье.

Сравнивая формулы преобразований Лапласа и Фурье, заключаем, что преобразование Фурье является частным случаем преобразования Лапласа, т. е.

Поэтому рассмотренные формулы соответствия и свойства преобразования Лапласа справедливы и для преобразования Фурье.

Так, рассмотренный закон Ома в операторной форме теперь будет иметь вид.

Знаменатель этого выражения Z (yeo) = R + у col + 7— представляет со;

усоС бой комплексное сопротивление цепи, применявшееся для расчета цепей синусоидального тока (в установившемся режиме). В то же время это частотная характеристика двухполюсника, которая может быть получена экспериментально при установившемся режиме работы. Если входной сигнал имеет вид некоторого импульса, то, определив его спектр 5(yto) и зная частотную характеристику двухполюсника Z (jco), можно определить спектр тока /(усо) и потом переходной ток i (t). Аналогично для четырехполюсника, зная передаточную функцию /У (усо), можно определить спектр выходного сигнала:

и затем определить зависимость выходного сигнала от времени u₂(t).

Отметим, что спектр функции, передаточная функция и частотная характеристика цени, как и любая комплексная величина, могут быть представлены в нескольких видах, например:

где Н (со) — амплитудно-частотная характеристика (АЧХ); 0(со) — фазочастотная характеристика (ФЧХ).