Задачи для самостоятельного решения

Гамма-функция.

• 00
• 13.1. Используя выражение Г (а) = Jx^a₁e^-Xdx, где, а > 0, вычислить:

о.

• а) rfij; б) Г (1); в) Г (а + 1); г) Г (п + 1).
• 00
• 13.2. Найти величину интеграла Jx^e^dx, где, а > 0, если: a) к = 0;

о б) к = -1.

оо.

13.3. Найти величину интеграла Jx"e^-Xdx, если: а) а = 1,5; б) а = 5.

о.

13.4. Пусть случайная величина имеет плотность распределения вида.

• (однопараметрическое гамма-распределение). Найти константу С, математическое ожидание Мс, и дисперсию D?.
• 13.5. Пусть случайная величина имеет плотность распределения вида

• (двухпараметрическое гамма-распределение). Найти константу С, математическое ожидание Мс и дисперсию Db,.
• 13.6. Найти точечную оценку параметра а распределения

^х«» ¹ г г,.

-е~^х х>0

р₅(х, а) = < Г (а) ' ' Исследовать оценку на несмещенность.

О, х <0.

13.7. Найти точечную несмещенную оценку параметра X показатель;

з ного распределения, если известно, что случайная величина ?, = где.

i=l.

^ ~ Exp (X), имеет распределение.

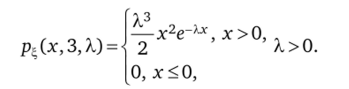
13.8. Проверить эффективность выборочной характеристики.

Х^п

л л~ 1 2 -х>0.

Х-несм ⁼-— гамма-распределения pJx, n, X)=< Г (п) ' 'пе.

^{П Х} [о, х<0,.

eN, >.>0.

Распределение Пирсона.

• 13.9. Доказать, что сумма двух независимых случайных величин, имеющих распределение Пирсона, также подчиняется распределению Пирсона.
• 13.10. Случайная величина Хп распределена по закону х² с числом степеней свободы п = 2. Найти вероятность Р (1 < Хп < 2).
• 13.11. Найти математическое ожидание распределения Пирсона.

ззо.

• 13.12. Найти дисперсию распределения Пирсона.
• 13.13. Доказать, что распределение Пирсона асимптотически нормально.
• 13.14. Пусть случайная величина г| подчиняется нормальному закону распределения: г) ~ JV (0, 1). Найти функцию плотности случайной величины? = г|².
• 13.15. Пусть случайная величина ц подчиняется нормальному закону распределения: r ~ N (0,1). Найти функцию плотности случайной величины ^ = ^~.
• 2
• 13.16. Найти оценку для числа степеней свободы г распределения у}. Найти дисперсию этой оценки. Исследовать полученную оценку на несмещенность.
• 13.17. В двухпараметрическом гамма-распределении р_?(х, аД) = А."
• -x^a~^c~'^/JC х > О,

= Г (а) ' ' а > О, X > 0 подобрать значения параметров, при О, х < О, которых гамма-распределение вырождается: а) в показательное распределение; б) распределение Пирсона.

Распределение Стьюдента.

13.18. Пусть § 0, ?], ^₂. •••> — независимые, нормально распреде;

П ленные случайные величины, ~ N (0, а²), и ? Найти распре;

V ^п i=i.

деление случайной величины у=—.

Л.

• 13.19. Случайная величина t_n имеет распределение Стьюдента с п = 1. Найти вероятность P (t" < 1).
• 13.20. Функция распределения Стьюдента при п = 1 описывает распределение Коши. Найти плотность этого распределения, его математическое ожидание и дисперсию.
• 13.21. Доказать, что распределение Стьюдента с ростом числа степеней свободы сходится к нормальному.
• 13.22. Найти оценку для числа степеней свободы г распределения Стьюдента. При каких г это возможно?

Распределение Фишера.

• 13.23. Пусть i;₂, •••> ^и Ли Лг> •••> Лт — независимые, нормально распределенные случайные величины, ~ N (0, 1), r)_;— ~ N (0, 1). Найти
• 1 п i т

закон распределения случайной величины у = — У &/—Тггё.

п Ы1 т _jml ¹

• 13.24. Пусть случайная величина? имеет распределение Стьюдента с п степенями свободы. Какое распределение имеет случайная величина Г| = ^²?
• 13.25. Случайная величина/, _т имеет распределение Фишера спит степенями свободы. Найти распределение случайной величины
• 1

^п, т ~ г

• 1п, т
• 13.26. Случайная величина/, _т имеет распределение Фишера с п и т степенями свободы. Найти распределение случайной величины
• 13.27. Случайная величина/ «, имеет распределение Фишера спит степенями свободы. Какой вид имеет случайная величина %=/ ^ при т —>оо? Найти математическое ожидание и дисперсию этой случайной величины.
• 13.28. Случайная величина/, _т имеет распределение Фишера с п = 1, т = 1. Найти вероятность Р (0 < / _т < 3).
• 13.29. Случайные величины распределены нормально с одинаковыми дисперсиями. Найти вероятность того, что их выборочные дисперсии, построенные по двум наблюдениям, будут отличаться более чем в девять раз.
• 13.30. При каких условиях, наложенных на п и т, распределение Фишера можно приближенно заменить нормальным распределением?

Теорема Фишера.

• 13.31. Найти дисперсию исправленной выборочной дисперсии S², построенной по случайной выборке объемом п из нормальной генеральной совокупности N (a, ст²).
• 13.32. Найти дисперсию неисправленной выборочной дисперсии а², построенной по случайной выборке объемом п из нормальной генеральной совокупности N (a, a²).
• 13.33. Пусть независимые выборки х_1г х₂, …, х" ~ N (aа²) и у_1г

S²

У2> •••> Ут ~ W (a₂, а²). Доказать, что статистика /__{l m}_i =-±- распределена по закону Фишера сп-1ит-1 степенями свободы.

13.34. Пусть даны независимые выборки х₁, х₂, ???, х_п ~N (a, of)

S² ст²

и У1, У2>->Ут ~JV (a, a^). Доказать, что статистика /_n__1>m__a =^-7 рас;

S² а²

пределена по закону Фишера сп-1иш-1 степенями свободы.

х — а I—.

13.35. Доказать, что случайная величина t=——vn, построенная.

S_n

по выборке из нормальной генеральной совокупности N (a, ст²) с известным математическим ожиданием и неизвестной дисперсией, распределена по закону Стьюдента с п — 1 степенями свободы.

• 13.36. Доказать асимптотическую эффективность несмещенной оценки генеральной дисперсии в случае нормального распределения.
• 13.37. Пусть лг_1; х₂, …, х_п иу₁, у₂, …, у_т — случайные выборки объемами пит соответственно из нормально распределенной генеральной совокупности N (a, а²) с исправленными выборочными дисперсиями S²

и S² Доказать, что исправленная выборочная дисперсия S² _у =—-х.

п + т-2

x[(n-l)S² +(m-l)S²)], построенная по всем наблюдениям, является несмещенной и асимптотически эффективной оценкой теоретической дисперсии а².

• 13.38. Найти закон распределения суммы случайных величин
• (n-l)S² (m-l)S²

а² а²

• 13.39. Пусть имеется к случайных выборок объемами п" где i = 1, 2, …, к, из нормально распределенной генеральной совокупности N (a, a²) с исправленными выборочными дисперсиями Sf. Найти эффективную оценку для дисперсии а².
• 13.40. Пусть независимые выборки х_г, х₂, …, х_п иу_ьу₂, …, у" взяты из одной генеральной совокупности N (a, а²). Доказать, что разность

средних ху ~N⁰, —a²j.

13.41. Пусть Xj, х₂, …, х_п иу_ьу₂, …, у_т — случайные выборки объемами п и т из нормально распределенной генеральной совокупности N (a, о²) с исправленными выборочными дисперсиями S² и S². Доказать,.

х-у

что статистика-. — распределена по закону.

fTT (n-l)S²+(m-l)S²

Vn mV п + т-2

Стьюдента с п + т-2 степенями свободы.

• 13.42. Пусть х_г, х₂, …, х_п ну_1гу₂, …, у_п — случайные выборки объемом п из нормально распределенной генеральной совокупности N (a, а²) с исправленными выборочными дисперсиями S% и S². Построить распределение разности средних. Указать закон распределения.
• 13.43. Показать, что если оценка 0″ эффективна, то ее дисперсия

д 1.

имеет вид DQ_n—.

п

13.44. Привести пример неэффективной оценки 0," дисперсия которой обратно пропорциональна числу наблюдений.

• 13.45. Доказать, что х является эффективной оценкой для параметра р биномиального распределения P (?, = rn) = c™p^mqⁿ-^m.
• 13.46. Для оценивания среднеквадратического отклонения а нор-

Л 1 ^П

мального распределения N (0, а²) получена оценка <�т_п = а— У | х_; |. Полу;

^1.

чить несмещенную оценку а_несм и исследовать ее на эффективность.

• 13.47. Пусть выборка х_1; х₂, …, х_п произведена из генеральной совокупности с равномерным распределением на интервале (0, 0). Найдена смещенная оценка параметра 0: 0″ = х_тах, которая затем исправлена. Как изменится при этом дисперсия оценки?
• 13.48. Пусть выборках_х, х₂, …, х" произведена из генеральной совокупности с равномерным распределением на интервале (0, 0). Предложены две несмещенные и состоятельные оценки 0j = [ 1 н—|х_тах и0₂=2х параметра 0. Сравнить их дисперсии. ^ ^п?
• 13.49. Пусть выборках], х₂, х_п произведена из генеральной совокупности с равномерным распределением на интервале (0, 0). Предложены оценки 0j =fl+—jx_max и 0₂ =2х параметра 0. Провести сравнительный анализ качества оценок: несмещенность, состоятельность, эффективность, асимптотическая нормальность.
• 13.50. Случайные величины Г|₂ ~ N (0,1), независимы и являются

функциями случайных величин ?,_ь %₂: ^ + а?₂ и Г|₂ = - а?₂. Являются ли ?,_ь ?,₂ независимыми случайными величинами и как они распределены?

П

13.51. Доказать, что па% = Ух? -пх².

i=i.

П _л

13.52. Доказать, что ух? =пх² +(n-l)S².

i=i.

13.53. Доказать, что Р{%² < х} = Ф (л/2х — /2п).