Множества. 
Алгебра множеств. 
Отношения на множествах. 
Отображения множеств

Аксиомы равенства. Классы равенств

В математических рассуждениях вне зависимости от уровня формализованное™ текста наиболее часто употребляется отношение равенства. При формализованном описании математических теорий отношение равенства описывается аксиомами, утверждающими рефлексивность равенства и возможность замены равного равным (см. Пример 1.1 в п. 1.5).

Из аксиом отношения равенства вытекают такие его свойства:

• 1) а = а;
• 2) если а = Ь, то b = а;
• 3) если а = Ь и Ь = с, то а = с,

где а, Ь, с — объекты одной природы, или, говоря более точно, символы переменных, у которых общее множество значений.

С логической точки зрения можно выделить три класса равенств:

I. Аксиомы (см. пп. 4.5 и 5.2).

II. Утверждения — логические следствия аксиом:

На. Тождества — равенства, справедливые в силу аксиом при всех значениях входящих в них переменных:

Пб. Теоремы — равенства, являющиеся следствием аксиом при некоторых дополнительных условиях, ограничениях на входящие в эти равенства переменные: а² +Ь² =с², если а, Ь, с — длины соответствующих сторон прямоугольного треугольника.

III. Определения:

Ша. Явные определения, вводящие новый символ: 1 + 1=2, Va > 0 я ⁰ = 1. Шб. Неявные определения — уравнения'.

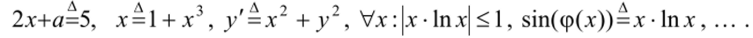
Изложенное выше описание отношения равенство является достаточным для нашего не очень формализованного изложения, и мы будем заменять символы = и = на символ = там, где это не вызовет недоразумений.

Множество элементов

Традиционная математика, элементы которой мы здесь излагаем, оперирует объектами четырех типов: множествами, функциями, отношениями и свойствами. Объекты трех из четырех типов могут быть сведены к объектам четвертого типа. Мы за исходное понятие принимаем понятие множества. Создатель теории множеств [32] немецкий математик Георг Кантор (3.03.1845−6.01.1918) говорил, что «множество — это соединение в целое определенных различных объектов нашей интуиции или нашего мышления». Мы называем эти объекты точками или элементами множества, и записи а е М и ЬёМ означают, что элемент а принадлежит множеству М, а элемент b не является элементом множества М.

Мы не будем ставить теорию множеств на аксиоматическую основу и перечислим некоторые принципы, не заботясь об их полноте и независимости.

1. Каждое множество определяется своими элементами: множества, А и В называются равными, если они состоят из одних и тех же элементов, или в символической записи:

• 2. Мно.жество 0, не содержащее никаких элементов, называется пустым и вводится для формальной записи пустоты (М = 0) и непустоты (М Ф 0) множества М.
• 3. Для любых множеств Р и О существует множество С, единственными элементами которого являются Р и Q, т. е. С = {P, Q}.

Из этого принципа существования двухэлементного множества при Р = Q следует существование одноэлементного множества.

4. Как аксиому принимаем, что никакое множество не является элементом самого себя, т. е. УМ М

В силу этого принципа теоремой будет выбор, а Ф {а} из альтернативы, а = {а} или, а Ф {а}. Действительно, если мы обозначим множество {а} через Л/, тогда из аеМ = {а} = а следует, что аеа.

Определение 3.1. Множество, А называется подмножеством множества М, если оно содержит элементы из множества М и никаких иных.

Формальная запись A d М означает нестрогое включение А во множество Л/, т. е. допускает совпадение множеств А и М. В этом случае множество А называется несобственным подмножеством множества М. Запись Ad М означает строгое включение, при котором А ф М . В этом случае подмножество А называется собственным подмножеством множества М. Для каждого множества М по определению 0 сМ .

5. Существует множество Р (М) всех подмножеств множества М, называемое степенью множества М.

Формальная запись Р (М)={А: А сМ}.

Иногда степень множества обозначают символом 2^м, по аналогии с известным фактом из теории конечных множеств, где данным символом обозначается количество всевозможных подмножеств конечного множества М. Отметим, что во фразе А с М по крайней мере одной из букв обозначено переменное множество.

Конкретные множества мы будем задавать одним из следующих способов:

I. Непосредственным перечислением элементов: 5={^}, М = {0},.

Q = {ц, ы, п, л, е, н о, к, 0, ж, а, р, е, н, ы, й}. Здесь Ми S суть одноэлементные множества, а множество Q содержит 16 элементов.

II. Указанием характеристического, определяющего данное множество свойства: Р = {у: 0 <�у < 1}, М{х: Л (х)}. Во множество М входят те и только те элементы х, которые обладают свойством R(), см. Аксиому 7 п. 3.7.3.

III. В = {0,1, 2,…, 9}, 7V = {1,2,3, S = {a, b_y с,…}. Три точки означают пропущенные или недописанные по каким-то причинам элементы, сущность которых ясна читателю из его предыдущего опыта, а множество S содержит элементы а, Ь, с и еще какие-то элементы.

Упражнение 3.1. Перечислить вес подмножества следующих множеств: А = {а, Ь), С = {х, у, z}, D = {0,1,2,3}.

Верно ли утверждение, что количество N всех подмножеств А я-элементного множества М равно числу N = 2″ (см. Определение 3.1)?