Умение контролировать собственную деятельность

Одним из условий, влияющих на успешность учебной деятельности учащихся, является их способность к самоконтролю: умение своевременно подмечать и устранять ошибки, предвидеть возможные трудности в решении возникших проблем, оценивать и обобщать положительные стороны своей учебной работы и т. п.

Тем не менее многие учащиеся и учителя считают, что функция контроля и оценивания принадлежит исключительно учителю. Любопытный пример в этом плане приводит В. И. Рыжик: «Однажды в двух девятых классах в начале учебного года была проведена письменная работа по повторению. Ученикам, допустившим ошибки при выполнении заданий, было предложено найти их. Результат был таков — из 38 учеников смогли справиться с заданием только 2, остальные, так и не найдя допущенных ошибок, стали решать задачи заново» (Рыжик, 1980, с. 46). О том, что формированию умения осуществлять контроль собственной деятельности не уделяется должного внимания, говорят исследования, проведенные Л. В. Жаровой, При ответе на вопрос: «Проверяете ли вы себя при выполнении самостоятельной работы?», ею были получены следующие результаты: постоянно контролируют свою деятельность только 18% подростков и 26% старшеклассников от общего числа опрошенных. Больше половины ответивших проводят самоконтроль эпизодически, нерегулярно. Выделяется группа школьников, которые никогда не проверяют выполненные учебные задания (Жарова, 1993).

Важность и необходимость формирования у учащихся умения осуществлять самоконтроль постоянно обсуждаются в исследованиях в области математического образования. Так, например, С. М. Чуканцев отмечает, что «самоконтролю надо учить учащихся так же, как мы учим их, например, решать задачи или доказывать теоремы. Важно также, чтобы учащиеся видели и собственное положительное отношение учителя к самоконтролю» (Чуканцев, 1979, с. 51).

Во многих современных моделях обучения умению осуществлять самоконтроль уделяется особое внимание. Например, в «развивающей модели» обучения умение осуществлять самоконтроль входит в оценку уровня сформированности учебной деятельности. В. В. Давыдов пишет о необходимости формирования у учащихся умения учиться, где одним из компонентов является умение осуществлять самоконтроль (Давыдов, 1996).

В исследованиях Г. В. Репкиной и Е. В. Заики выделены уровни сформированности действия контроля. В основу классификации этих уровней положены возможности учащихся в способах оценки своей учебной деятельности как при работе с новой задачей, так и при выполпенни освоенных или неоднократно повторенных действий. Особое внимание Г. В. Репкина и Е. В. Заика обращают на умение учащихся работать с ошибками — находить их по просьбе взрослого или самостоятельно, объяснять причину возникновения ошибки и исправлять ее (Репкина, Заика, 2003).

Одним из дидактических принципов системы Л. В. Занкова является «осознание учащимися процесса учения», Этот принцип предполагает «…концентрирование внимания детей не только на вопросах: „Что изучается?“ и „Понимаю ли я то, что изучаю?“, но и на вопросах; „Зачем я это изучаю?“, „Как то, что я изучаю сейчас, связано с тем, что я уже знаю?“, „Что привело меня к ошибке и как я должен действовать, чтобы ошибок больше не было?“» (Аргинская, 1995, с. 11).

В работах Л. О. Денищевой, Н. Ю. Лизуры, Л. А. Лошкаревой, С. Г. Манвелова, В. А. Осинской, А. К. Осницкого, Н. А. Тарасенковой, Л. М. Фридмана, П. М. Эрдниева рассматриваются процедуры, которые могут быть включены в педагогический процесс развития навыков самоконтроля. Так, например, С. Г. Манвеловым предложена схема (рис. 5), отражающая возможность перехода от внешнего контроля к самоконтролю (Манвелов, 1997, с. 141).

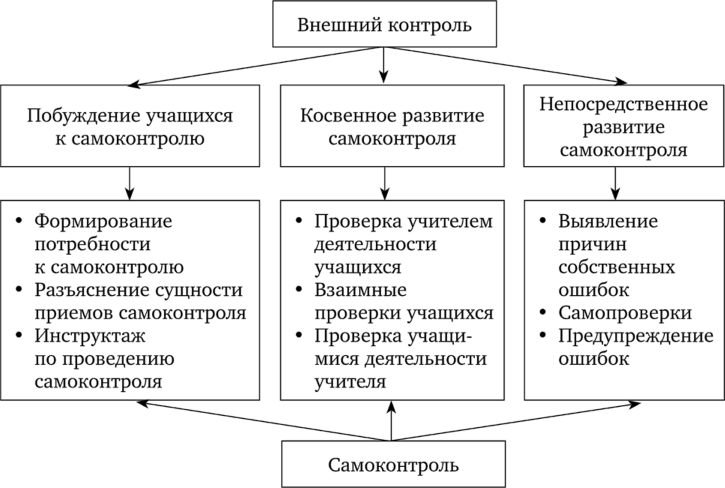
Рис. 5. Схема перехода от внешнего контроля к самоконтролю.

Данная схема дает возможность определить некоторые требования к учебным текстам, способствующим формированию у учащихся опыта осуществлять самоконтроль, причем этот опыт должен постепенно обогащаться средствами учебных текстов разных типов.

Рассмотрим некоторые типы текстов, которые знакомят школьников со способами самоконтроля и развивают у них способность осуществлять разные формы самоконтроля интеллектуальной деятельности.

Прежде всего, нужны тексты, которые помогали бы школьникам научиться приемам осуществления контроля в рамках отдельных тем. К таким типам текстов относится «текст — способы самоконтроля». Приведем фрагменты текстов, дающих учащимся возможность выработать приемы самоконтроля. В частности, особое внимание было уделено постановке обратных задач как средства организации самоконтроля. Через специальные тексты учащиеся могут выделить этот прием контроля для проверки взаимосвязанных действий (тема «Натуральные числа и десятичные дроби», 5-й класс).

1) Составьте задачи по предложенным решениям:

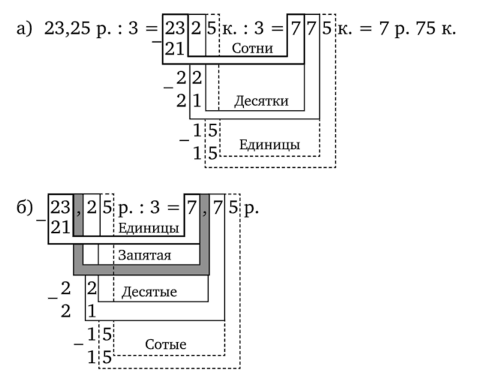
• 2) Проверьте результаты:
  • • сложением;
  • • вычитанием;
  • • умножением;
  • • делением.
  • (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 276.)

Работая над этими текстами, учащиеся должны обратиться к определениям действий деления и умножения, обосновывая способы проверки.

Аналогичная работа проводится в курсе алгебры. Приведем фрагменты таких текстов (тема «Знакомимся с алгеброй», 7-й класс).

Проверьте, правильно ли выполнено деление:

• 1) 39am : 13 = 3am;
• 2) 3a: a = 3;
• *?
• 3) 3—cz: 3 = 1—cz ;
• 11 11
• 4) 50np: (2p) = 25n;
• 5) x⁸y: (x⁵y) = x³;
• 6) 26x⁴y²: (2x³y) = 13xy;
• 7) (5a + 5b — 5c): 5 = (a + b — c);
• 8) (6ax — 9bx — 15x): (3x) = 2a — 3b — 5;
• 9) (95ax + 133ax² — 76a²x — 209a²x²) : (19ax) = 5 + lx — 4a — llax;
• 10) (am — bm): (a — b) = m;
• 11) (x² — 8x + 7): (x — 7) = x — 1;
• 12) (2a² + 2a²b + 2ab² + 2b³): (2a² + 2b²) = a + b.
• (Знакомимся с алгеброй, 2004, c. 177.)

Проверьте, правильно ли выполнено разложение на множители:

• 1) 1992 = 23−3-83;
• 2) 40аЪ² = 4Ъ • ЮаЪ = 40аЪ • Ъ = 2 • 20аЬ²;
• 3) 2с² — Зс = с (2с — 3);
• 4) х² + х — 6 = (х — 2)(х + 3);
• 5) ах + ay + bx + by = (а + Ь)(х + у);
• 6) а² — Ь² = (а-Ь)(а + Ь).
• (Знакомимся с алгеброй, 2004, с. 160.)

Среди приемов самоконтроля средствами учебного текста можно отметить прием «примерной оценки искомых результатов», то есть оценка результатов с точки зрения здравого смысла. С этим приемом учащиеся знакомятся с помощью специальных заданий.

Округлите сумму до целых, десятых, сотых. Результаты запишите в таблицу.

• • 0,1 + 0,239 + 0,17;
• • 57,2 + 2,4 + 7,314;
• • 15,27 + 0,033 + 6,5.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 236.).

Не вычисляя произведение, запишите два натуральных числа, между которыми оно находится:

• 1) 12,9 • 3,4;
• 2) 4,6 • 2,54;
• 3) 27,25 • 4,7;
• 4) 0,37 • 97,8;
• 5) 25,1 • 3,98 • 1,05;
• 6) 0,27 • 0,68 • 0,9.

Сделайте проверку.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 261.).

Не производя точных вычислений суммы (1,5702 + 2,13 547), исключите неверные ответы: 37,15 671; 3,71 567; 2,61 504; 3,61 504.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 236.).

Как показать, что неравенства решены неверно?

• 1) х² + 5х-36 < 0, х е [-4; 9];
• 2) 40 + х — Зх² < 0, х е^-оо; -l^-ju (2; + оо);
• 3) -л/1з7х²+137>0,хеЯ.
• (Квадратичная функция, 2004, с. 143.)

При обсуждении таких заданий желательно, чтобы учащиеся построили программу своих действий: исключили те ответы, которые сразу бросаются в глаза как неверные, привели возможные основания для выбора оставшихся.

Как известно, одной из сложных операций для учащихся является деление натуральных и десятичных дробей. Они затрудняются в подборе цифр в частном, постановке запятой в частном и т. д. Так, рассматривая «трудные» случаи деления натуральных чисел, Е. С. Березанская отмечает, что нужно обратить особое внимание учащихся на случай деления чисел, когда в частном получается число, в записи которого имеется один или несколько нулей в середине. Далее Березанская советует «следить за тем, во-первых, чтобы учащийся определил заранее, сколькими цифрами будет записано частное, а потом проверил, совпадает ли ответ с его предварительным подсчетом; во-вторых, чтобы учащийся, снося единицы какого-либо разряда в остаток и получая промежуточное делимое, которое не делится на делитель, не забывал записывать 0 на месте соответствующего разряда в частном» (Березанская, 1922, с. 156).

В связи с этим можно привести фрагменты текстов, которые помогают школьникам научиться «прикидывать» результаты деления (тема «Натуральные числа и десятичные дроби», 5-й класс).

Замените звездочки цифрами:

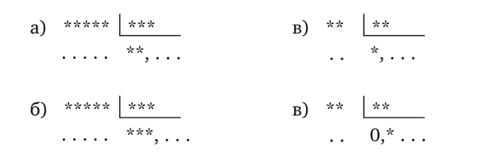
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, с. 276).

Составьте такие примеры деления, чтобы в частном получилось:

• а) один знак до запятой;
• б) два знака до запятой;
• в) три знака до запятой.
• (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 275.)

При работе с уравнениями, неравенствами, функциями учащиеся осуществляют проверку, исходя из определений соответствующих понятий, их свойств. Формирование ориентиров в такой деятельности осуществляется с помощью текстов, где обсуждаются возможные способы проверки. Приведем три примера таких текстов. Первый из них взят из темы «Квадратичная функция», раздел «Знакомимся с системами уравнений» (6-й класс).

Какие из следующих утверждений верны?

1. При решении систем уравнений нужно всегда делать проверку — подставлять найденные решения в уравнения системы.

• 2. При решении системы уравнений методом подстановки проверку можно не делать.
• 3. При возведении обеих частей одного из уравнений системы в квадрат всегда нужно делать проверку.
• 4. При делении обеих частей одного из уравнений системы на выражение, содержащее переменную, или при почленном делении одного уравнения на другое проверку можно не делать.
• (Квадратичная функция, 2004, с. 260.)

В итоге работы над этим текстом учащиеся должны вернуться к определению равносильности систем уравнений и оформить памятку по осуществлению самопроверки при их решении.

Еще одним важным видом умения контролировать собственную деятельность является умение видеть ошибки, сознательно избегать возможных ошибок. По этому поводу А. М. Матюшкин пишет: «Очень важно приучить ребенка не бояться допускаемых им ошибок и не стремиться исправлять ошибку учащегося с помощью нравоучений. Боязнь допустить ошибку сковывает инициативу ученика в постановке и решении им интеллектуальных проблем» (Матюшкин, 1972, с. 83).

Э. Фишбейн и А. Барам рекомендуют использовать так называемый «метод конфликтов», предлагая учащимся анализировать неправильные ответы, намеренно создавая ситуации, в которых им придется выяснить возможные причины допущенных ошибок (Fischbein, 1987; Barash, 2002).

Действительно, анализ ошибок помогает школьникам быть чувствительными к проблемам, задает им «болевые» точки, знание которых является профилактикой ошибочных действий. Такой тип учебных текстов можно назвать «текст — поиск ошибок». Приведем фрагменты подобных текстов. Первый текст предназначен для учеников 5-го класса (тема «Натуральные числа и десятичные дроби»).

При вычислении следующих сумм допущено не менее двух ошибок. Найдите их.

• а) 4,81 + 0,607 = 5,417;
• б) 3,12 + 1 — 3,22;
• в) 11,54 + 0,368 = 11,908;
• г) 0,3 + 0,08 = 0,11.
• (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 235.)

При выполнении данного задания важно обсудить пути поиска ошибок. При этом необходимо выделить случаи, которые явно бросаются в глаза, и подумать о способах проверки в других случаях.

Следующий фрагмент текста учит поиску ошибок в выполнении математических процедур (тема «Квадратичная функция», 9-й класс).

Найдите ошибку в решении неравенства 4 — х² > (2 + х)².

Решение:

(2 — х)(2 + х) > (2 + х)² |: (2 + х);

• 2 — x > 2 + x;
• 2x < 0] x < 0.

Ответ: (—со; 0).

В чем причина ошибки? Дайте правильное решение неравенства.

Составьте задание, предупреждающее ошибки в решении неравенств второй степени.

(Квадратичная функция, 2004, с. 142.).

Заметим, что после нахождения ошибок и объяснения причин их появления очень важно, чтобы учащиеся привели правильные решения, обосновывая их. Это придаст им уверенность в своих дальнейших действиях.

При изучении графиков функций важно, чтобы у учащихся были сформированы ориентиры, позволяющие им проконтролировать правильность выполненных построений. К таким ориентирам можно отнести: выделение точек пересечения графиков функций с осями координат, расположение угла наклона прямой к оси абсцисс, расположение графика на координатной плоскости, направление ветвей параболы.

Приведем пример таких текстов, используемых при изучении графиков линейной и квадратичной функций (тема «Функция», 9-й класс).

Три ученика построили графики функцииу = -2,5х следующим образом:

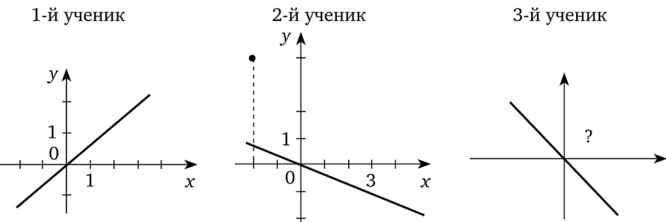
Учитель, посмотрев работы, сразу определил, что у первого ученика ошибка. Для проверки работы второго ученика он сделал дополнительные построения и выявил ошибку. На третьей работе он поставил большой вопрос.

Объясните, какие ошибки допустили ученики.

Как можно проконтролировать себя при построении графика функцииу = кх? (Функция, 2004, с. 221—222.).

Обсуждая причины ошибок в каждом случае, учащиеся обращают внимание на то, что учитель у первого ученика нашел ошибку сразу. Это следовало из расположения графика на координатной плоскости. График функцииу = — 2,5х должен быть расположен во второй и четвертой четвертях.

Дополнительные построения при анализе работы второго ученика позволяют увидеть у него ошибку: при х = 1, у Ф —2,5. Это дает учащимся еще один ориентир для организации самопроверки при построении графика прямой пропорциональности.

В третьей работе не соблюдены требования к построению системы координат. Задача для оценки такого графика становится неопределенной.

Приведем фрагмент текста, позволяющего выбирать ориентиры контроля при построении графика квадратичной функции (тема «Квадратичная функция», 9-й класс).

Ученик построил график функции у = 2х² — 12х + 18.

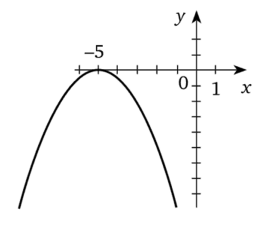
Верно ли построен график?

На какие свойства графика вы обратите внимание, отвечая на этот вопрос? Выясните, существуют ли точки графика, не удовлетворяющие уравнению у = 2х² — 12х + 18?

Обратите внимание на направление ветвей параболы, на точки пересечения с осями координат, на координаты вершины.

Если вы считаете, что график построен неверно, то постройте его правильно.

(Квадратичная функция, 2004, с. 87).

К текстам, стимулирующим учащихся проверить себя, относятся игры с жесткими правилами: «домино», «лото», «лабиринт», «зашифрованное слово» и т. п. В рамках этих текстов у учащихся имеется возможность узнать, правильный ли получен результат, и в случае неудачи начать поиск ошибок. Приведем пример одной из таких игр (тема «Натуральные числа и десятичные дроби», 5-й класс).

Выполните деление десятичной дроби на натуральное число:

• 17,85 :17;
• 1,2369: 93;
• 183,6: 204;
• 86,448: 80.

Используя шифр, расставьте у результатов деления соответствующие буквы и прочитайте запрятанное в задании слово:

Как вы думаете, почему зашифровали именно это слово? (Математика-5. Ч. 2. Натуральные числа и десятичные дроби, с. 276.).

Полнота контроля и мотивация к его осуществлению во многом зависят от того, как себе представляет ученик желаемый результат, то есть каков у него образ результата действия, насколько он видит пространство возможных затруднений и ошибок.

Важной стороной этой деятельности является готовность оценивать адекватность найденного результата решения задачи ее условию. Многие учащиеся, как отмечается в различных исследованиях, не имеют привычки проводить анализ полученных результатов (особенно ярко эта особенность проявляется при решении текстовых задач). Так, 3. П. Матушкина приводит следующий пример: «Не только учащиеся, ио и студенты — будущие учителя, как правило, „успешно“ решают задачу: „В трех баках было вместе 50 литров бензина, причем в первом баке было на 10 литров больше, чем во втором. Когда из первого бака вылили в третий 26 литров, во втором и третьем стало поровну. Сколько бензина было в первом баке?“ Составив уравнение: х — 10 = (50 — х — - (х — 10)) + 26 и получив ответ: в первом баке было 32 литра, учащиеся не сомневаются в его реальности. На самом же деле данная задача не имеет решения» (Матушкина, 2003, с. 74).

Приведем примеры двух текстов, в которых учащимся предлагается проанализировать действия над математическими объектами с точки зрения предупреждения возможных ошибок. Рассмотрим фрагмент текста, посвященный анализу преобразований, выполняемых над уравнениями (тема «Алгебраические дроби», 7-й класс).

Решите уравнения:

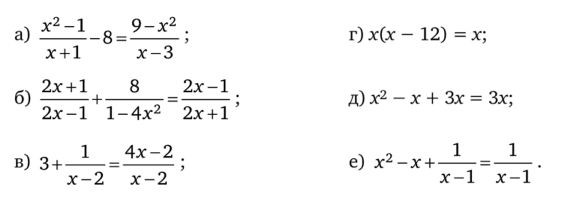
Какие преобразования вы при этом выполняли:

• а) переносили слагаемые из одной части уравнения в другую;
• б) умножали (делили) обе части уравнения на одно и то же число, не равное нулю;
• в) осуществляли приведение подобных целых алгебраических выражений;
• г) умножали обе части уравнения на целое алгебраическое выражение;
• д) делили обе части уравнения на алгебраическое выражение;
• е) иные преобразования?

Какие из преобразований, на ваш взгляд, позволяют переходить от данного уравнения к равносильному ему уравнению? Какие из них могут привести к уравнению, не равносильному исходному?

(Алгебраические дроби, 2003, с. 177.).

Работу над этим текстом желательно построить как протокольную (то есть все дети выполняют задания и отвечают на вопросы в письменном виде). Важно увидеть самостоятельные решения учащихся, их выводы, а затем провести обсуждение в классе. Можно устроить и «провокацию», предложив для обсуждения неверные решения некоторых из данных уравнений. В итоге полезно назвать список преобразований, которые следует выполнять с осторожностью. Приведем фрагмент еще одного текста этого типа:

Выберите верные утверждения:

• 1. Произведение всегда больше каждого из множителей.
• 2. Произведение не всегда больше каждого из множителей.
• 3. Если один из множителей меньше единицы, то и произведение меньше единицы.
• 4. Если каждый из множителей меньше единицы, то произведение обязательно меньше единицы.

Ложные высказывания опровергните с помощью примеров.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2005, с. 260.).

В каждом из этих текстов учащимся предлагается подвергнуть анализу результаты выполненных действий. Работа с подобными текстами поможет школьникам в проведении контроля собственной умственной деятельности, так как мобилизует их внимание на анализ результатов собственных действий.

Опыт учащихся по поиску способов контроля может быть обобщен в специальных текстах, которые были названы «текст — выбор способа самоконтроля». Приведем фрагмент такого типа текстов по теме «Натуральные числа и десятичные дроби» (5-й класс).

Как бы вы стали проверять решение любого примера на сложение и вычитание? Окажутся ли полезными для вас такие советы:

• 1) при сложении и вычитании в столбик сохраняйте позицию запятой;
• 2) делайте проверку сложения перестановкой слагаемых, проверку вычитания — сложением;
• 3) делайте приближенную оценку результата.

Что бы вы добавили к этим советам?

В какой последовательности вы бы стали им следовать?

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 236.).

Рассмотренные нами тексты дают возможность учащимся осуществлять выборочный самоконтроль, развивают у них способность с одного взгляда оценивать предлагаемые решения. П. П. Блонским были выделены четыре стадии проявления самоконтроля применительно к усвоению материала. Первая стадия характеризуется отсутствием всякого самоконтроля. Вторая стадия — полный самоконтроль. На этой стадии учащиеся проверяют полноту и правильность усвоенного материала. Третья стадия — выборочный контроль. В этом случае учащийся контролирует, проверяет только главное по вопросам. На четвертой стадии видимый самоконтроль отсутствует, тем не менее он осуществляется на основе каких-то незначительных деталей (Блонский, 1979, с. 259—260). Подчеркнем, что именно на четвертой стадии происходит переход (интериоризация) произвольного интеллектуального контроля в непроизвольный интеллектуальный контроль, что может рассматриваться как особая форма обогащения метакогнитивного опыта учащихся и, соответственно, как свидетельство качественного роста их интеллектуальных возможностей.

Таким образом, к учебным текстам и заданиям, создающим условия для обогащения такого компонента метакогнитивного опыта, как способность контролировать собственную интеллектуальную деятельность, мы относим следующие:

• • текст — способы самоконтроля;
• • текст — поиск ошибок;
• • текст — выбор способа самоконтроля.