Формирование когнитивных схем математических понятий и способов математической деятельности

Когнитивная схема, с одной стороны, дает школьникам возможность хранить в памяти устойчивые, типичные характеристики изучаемых математических явлении, воспроизводить типичный пример данного класса объектов. С другой стороны, когнитивная схема должна стать основой для опознания нового понятия, создавать контекст для приобретения новых знаний. Наконец, когнитивная схема должна быть гибкой, чтобы… Читать ещё >
Формирование когнитивных схем математических понятий и способов математической деятельности (реферат, курсовая, диплом, контрольная)
Одним из показателей развития понятийного мышления является наличие у учащегося адекватных когнитивных схем. Под когнитивными схемами понимается такая форма организации и хранения прошлого опыта, которая позволяет учащимся активно включать его в решение возникающих проблем.
Когнитивная схема, с одной стороны, дает школьникам возможность хранить в памяти устойчивые, типичные характеристики изучаемых математических явлении, воспроизводить типичный пример данного класса объектов. С другой стороны, когнитивная схема должна стать основой для опознания нового понятия, создавать контекст для приобретения новых знаний. Наконец, когнитивная схема должна быть гибкой, чтобы интеллектуальное поведение могло адаптироваться к новым условиям деятельности.
Проблеме выделения разных видов когнитивных схем и их описанию посвящены исследования Дж. Брунера, Б. М. Величковского, М. С. Минского, У. Найссера, Ж. Пиаже и др. Рассмотрим назначение некоторых когнитивных схем в процессе изучения учащимися числовых систем.
Дж. Брунером введено понятие фокус-примера как прототипа, в котором сконцентрированы наиболее существенные признаки изучаемого объекта; примера, который дает возможность составить представление о классе изучаемых объектов, о сути изучаемого явления. Обсудим приемы организации такого типа текстов, которые получили название «текст — введение фокус-примера».
Так, в качестве фокус-примеров десятичных дробей с одним знаком после запятой могут быть использованы дроби 2,6 и 0,5, так как они являются прототипом данного класса десятичных дробей. Дробь 222,22 может стать фокус-примером десятичных дробей, так как, анализируя ее особенности, можно выделить важнейшее свойство десятичных дробей — в позиционных системах записи чисел значение цифры зависит от того, какую позицию в записи числа она занимает.
Далее, средствами текста создаются условия для того, чтобы учащиеся могли воспринять эту дробь как фокус-пример. В частности, эта дробь помещается в таблицу разрядов.
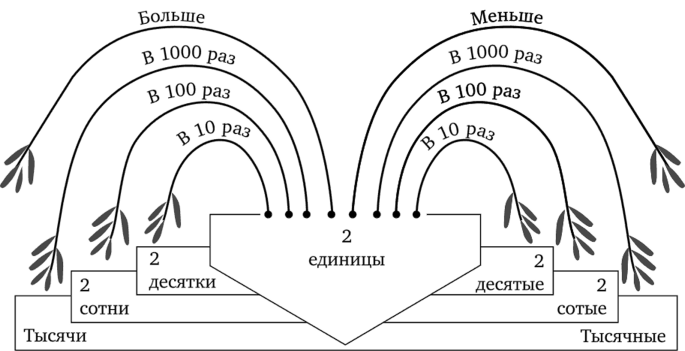
Тысячи. | Сотни. | Десятки. | Единицы. | '. | Десятые. | Сотые. | Тысячные. | Десятитысячные. |
Кроме того, используется рисунок-схема, на котором иллюстрируется свойство десятичных дробей.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 70.).
Наконец, в тексте предлагается своего рода визуальная модель, которая помогает учащимся сфокусировать свое внимание на существенных признаках данной дроби и тем самым запомнить особенности записи десятичных дробей.
- — Как красиво и просто: десятки — десятые, сотни — сотые, — сказала фрекен Снорк.
- — Что это просто, я согласен, но где ты увидела красоту? — возразил Снорк.
Фрекен Снорк укоризненно взглянула на брата и нарисовала картину.
— Смотри, Снорк, а запись-то десятичных дробей похожа на фонтан: «струи» симметрично бьют из единиц, — восхитился Муми-тролль.
Мудрая красота: если известно, как устроено число слева от запятой, то легко понять и устройство числа справа от запятой, — покивал головой Ондатр.
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 70.).
Особенно важен выбор фокус-примера при введении новой темы. Он должен попасть в зону ближайшего развития учащихся, стать основой для разворачивания собственных действий по использованию прошлых и новых знаний.
Так, фокус-пример понятия «отношения» может возникнуть при рассмотрении ситуаций, в которых приходится действовать по «рецепту».
Кондитер. В рецепте из поваренной книги написано: «Для приготовления вишневого варенья нужно взять сахар и вишню в весовом отношении 2: 3». Объясни мне, пожалуйста, сколько нужно взять сахара и сколько — вишни?
И что это такое — отношение?
Математик. Слова «взять в весовом отношении 2: 3» означают, что на каждые две весовые меры сахара нужно взять три весовые меры вишни. Кондитер. Так сколько сахара нужно взять?
Математик (улыбаясь). Сколько захочешь.
Кондитер. Замечательно! А вишни? Тоже сколько захочу?
Математик. Правильнее будет сказать, что ты волен выбрать единичную меру, которой будешь потом измерять и вес сахара, и вес вишни. Если ты за единичную меру выберешь один килограмм, то нужно будет взять 2 килограмма сахара и 3 килограмма вишни. Но ты можешь выбрать и любую другую меру.
Кондитер. Например, есть такая английская мера веса — фунт. Если выбрать за единицу меры ее, то нужно будет взять 2 фунта сахара и 3 фунта вишни. Правильно?
Математик. Совершенно верно. Скажи теперь, сколько нужно взять сахара и вишни, если за единичную меру принять не один фунт, а, например, три фунта?
Кондитер. Но разве можно принимать три фунта за одну единицу? Ведь три совсем не равно одному!
Математик. А почему бы и нет? Могу ведь я сказать: «одна трехфунтовая гиря». И мерить вес всех компонентов трехфунтовыми гирями.
Кондитер. Действительно… Но тогда надо рассуждать по-прежнему: возьмем 2 единицы сахара (что составит 3−2 = 6 фунтов) и 3 единицы вишни (что составит 3−3 = 9 фунтов).
Математик. Неважно, сколько здесь по отдельности берется сахара или вишни, а важно то, что они во всех случаях, когда варенье приготовлено по рецепту, сохраняют между собой одно и то же отношение.
Кондитер. А если взять сахара больше, что тогда произойдет?
(Математика-6. Ч. 2. Рациональные числа, 2005, с. 79—80.).
Еще одним видом когнитивных схем является фрейм. Фрейм — это форма хранения стереотипных знаний о некотором классе ситуаций: его «каркас» характеризуют устойчивые, всегда имеющие место отношения между элементами объекта или ситуации, а «узлы» (или слоты) этого каркаса — вариативные детали данного объекта или ситуации. Для формирования фреймов используется такой тип учебного текста, как «текст — создание фрейма». Для получения фреймов может быть использован прием варьирования действий с одним и тем же математическим объектом, например, при работе с понятием «позиционная запись числа». Одной из форм хранения стереотипных знаний о свойствах позиционной записи натурального числа является таблица разрядов. Ее разворачивание вправо приводит к появлению нового вида чисел — десятичных дробей (вариативность), при этом сохраняются известные свойства позиционной записи чисел (инвариантность).
Приведем фрагмент текста, с помощью которого создается когнитивная схема (фрейм) позиционной записи чисел (тема «Натуральные числа и десятичные дроби», 5-й класс).
Рассмотрите таблицу разрядов.
Тысячи | Сотни | Десят ки | Еди ницы | '. | Деся тые | Сотые | Тысяч ные | Десятиты сячные |
> | ||||||||
Какую закономерность в заполнении строк таблицы вы заметили? Как появился новый разряд?
Для чего нужна в таблице запятая?
Вы уже обратили внимание на то, что в таблице появилось новое число: 0,4 — нуль целых четыре десятых?
Это число называется десятичной дробью.
Объясните, как появилось это число в таблице разрядов.
Как бы вы заполнили следующую, пустую строку таблицы? (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 210.).
Возможность получения новых разрядов в записи десятичных дробей подчеркивается тем, что таблица разрядов изображается в тексте в виде рулона, и это способствует созданию у учащихся адекватной когнитивной схемы о взаимосвязях между натуральными числами и десятичными дробями, о свойствах десятичных дробей.

Следует заметить, что формированию фреймов способствуют тексты, содержащие вопросы, позволяющие выделить инвариантные и вариативные характеристики математических объектов. Приведем примеры подобных вопросов в теме «Делимость чисел» (6-й класс).
- 2. Может ли наименьшее общее кратное двух чисел:
- а) быть равным 0;
- б) быть равным 1;
- в) быть равным одному из чисел;
- г) быть больше каждого из чисел?
Проиллюстрируйте ответы примерами.
- 3. Как найти число, которое делится и на 72, и на 108?
- 4. Можно ли восстановить числа, если известны их наибольший общий делитель и наименьшее общее кратное?
- (Математика-6. Ч. 1. Делимость чисел, 2005, с. 112.)
Еще одним частным случаем когнитивных схем являются алгоритмы, инструкции, правила. Для формирования таких когнитивных схем был разработан тип текстов, получивший название «текст — процедура». Прежде всего сюда относятся тексты, в которых описываются основания соответствующих процедур.
В учебной книге «Математика-5. Ч. 1. Натуральные числа и десятичные дроби» предложено параллельное (совместное) изучение действий над натуральными числами и десятичными дробями. Такая форма организации учебного текста создает условия, позволяющие учащимся выявить основания для получения алгоритмов действий над десятичными дробями. Методическими приемами, способствующими выделению того общего, что объединяет алгоритмы действий над натуральными числами и десятичными дробями, является организация сравнения этих действий в условиях использования специальных визуальных средств и фокус-примеров.
Изучение деления многозначных натуральных чисел и десятичных дробей на однозначное число — это одна из сложных тем школьного курса арифметики. Причиной ошибок, допускаемых при ее изучении, является то, что учащиеся не осознают основную идею, — деление выполняется поразрядно.
Учебный текст начинается с задачи, мотивирующей поиск алгоритма деления десятичных дробей на однозначное число.
Как из доски длиной 1,48 м сделать 4 одинаковые полочки?
В тексте предлагается несколько решений: деление на основе практических соображений, деление на основе связей между единицами метрической системы мер, сведение деления десятичной дроби на однозначное число к делению многозначного числа на однозначное. Последнее решение дает возможность актуализировать известную учащимся процедуру деления натуральных чисел: «деление выполняется поразрядно». Причем эта когнитивная схема должна быть развернута достаточно полно, чтобы стать основой для формирования более сложной когнитивной схемы. Приведем фрагмент текста, содействующего актуализации опорной когнитивной схемы действия деления натуральных чисел.
Теперь делим поразрядно.
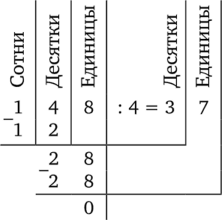
1 сотня нацело на 4 не делится, то есть в частном не будет цифры, стоящей в разряде сотен. А будут ли цифры в разряде десятков?
В делимом 14 десятков. 14 делится на 4. Получаем в частном 3 десятка. Из 14 десятков нацело разделилось 12 = 4 • 3.
- 2 десятка в остатке.
- 2 десятка переводим в единицы, получается 20 единиц, и присоединяем к ним 8 единиц делимого.
- 28 делится на 4 нацело. В частном получается 7, а в остатке 0. Деление закончено.
- — Получается, что Снусмумрик «распотрошил» число 148 на такие слагаемые, каждое из которых делится на 4, — сообразил Муми-тролль, — у него получилось:
- 148 = 12 дес. + 28 ед. = 120 + 28,
потом каждое слагаемое разделилось на 4:
- 148: 4 = (120 + 28): 4 = 120: 4 + 28: 4 = 30 + 7 = 37.
- (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 171.)
Данный текст восстанавливает в памяти учащихся алгоритм деления многозначного числа на однозначные. Затем предлагается текст, который вводит новые элементы (шаги) в алгоритм деления многозначного натурального числа на однозначное: деление многозначных натуральных чисел на однозначные, зная десятичные дроби, можно выполнить без остатка. При этом делимое в примерах текста остается прежним, а меняется лишь делитель.
Затем фрекен Снорк начала делить число 148 на 5. Вот что получилось:
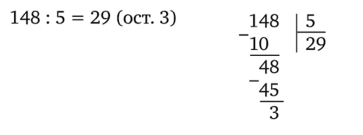
— А я попробую поделить в таблице разрядов. Оно как-то основательнее получается, — сообщил Муми-тролль, взял число 148, разделил его на 5 в таблице и записал ответ. Деление в таблице получилось без остатка, но появилась дробная часть:
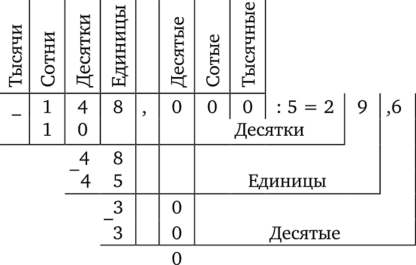
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 173.).
Деление вновь выполняется в таблице разрядов. Причем делимое остается прежним, а меняется лишь делитель. Это дает возможность учащимся увидеть общее и особенное в разных случаях деления натуральных чисел на однозначное число. Завершает текст вывод.
Если при делении натурального числа на однозначное натуральное число получается остаток, то ставь в частном запятую, а остаток переводи в единицы следующего, меньшего разряда и продолжай деление.
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 174.).
Следующий текст создает условия для формирования алгоритма деления десятичной дроби на однозначное число. Главное в данной когнитивной схеме — поразрядность деления, постановка запятой в частном. В связи с этим соответствующий текст вновь содержит таблицу разрядов. В приводимых примерах деления в делимом меняется лишь место запятой, а делитель остается одним и тем же. Это поможет школьникам увидеть закономерность в постановке запятой.
— Послушайте! — заметил Снусмумрик. — Так ведь если работать в таблице разрядов, то понятно, как делить десятичные дроби на однозначное число.
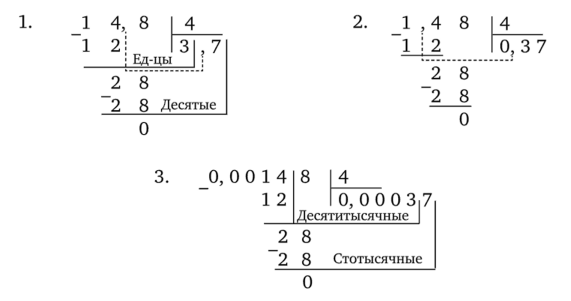
Деление десятичной дроби на однозначное натуральное число выполняем так же, как и деление натуральных чисел, но как только заканчивается деление целой части, в частном ставим запятую.
Если закончили «сносить» цифры делимого, а остаток еще не равен нулю, то последовательно приписываем в делимом справа один нуль за другим и продолжаем деление. Появление нуля в остатке означает, что деление закончено.
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 174.).
Для развития умений использовать алгоритм нужны тексты, которые позволяют учащимся осознать важнейшие его шаги. Приведем фрагмент одного из таких текстов о делении на однозначное число.
Рассмотрите равенства:
- 3208: 8 = 4 010; 0,3208: 8 = 40 100;
- 32,08: 8 = 4 010; 0,3 208: 8 = 40 100;
- 3,208: 8 = 40 100; 320 800: 8 = 401 000.
Поставьте запятую, отбросьте лишние нули.
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 175.).
Познавательная деятельность по получению когнитивной схемы — алгоритма — строится также на основе текстов, позволяющих учащимся приобретать знания о различных результатах, получаемых при его исполнении.
Приведем фрагмент текста, в котором создаются условия для обсуждения результатов выполнения деления многозначного числа и десятичных дробей на однозначное число: это может быть натуральное число, конечная десятичная дробь и бесконечная периодическая дробь.
У Тофслы с Вифслой с примерами 1,48: 9 и 148: 9 творилось что-то невообразимое.

Никто не мог понять, в чем тут дело, и тогда примеры 148: 9 и 1,48: 9 бросили в Волшебную Шляпу, и вот что получили в ответ:
148: 9 = 16,(4); 1,48: 9 = 0,16(4).
Тут вмешался Муми-папа:
- — Делить 148 и 1,48 на 9 столбиком можно сколь угодно долго, и процесс никогда не закончится. Припоминаю, что математики придумали для такого случая обозначение:
- 16,(4) и 0,16(4)
и название: бесконечные периодические дроби, число 4 — их период.
— Выходит, что при делении могут получиться и конечные десятичные дроби, и бесконечные периодические? — спросили хором Муми-тролль и Снусмумрик.
И Муми-папа ответил, что они, как никогда, правы.
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 175—176.).
С помощью создания и анализа парадоксальной ситуации, возникшей в тексте, учащиеся выходят на важный случай деления натуральных чисел и десятичных дробей.
Теперь необходимо составить целостную картину о результатах, получаемых при делении натуральных чисел. Приведем пример задания, в котором учащиеся учатся опознавать различные случаи деления в зависимости от полученных результатов.
Выполните деление и запишите результат в один из трех столбцов в зависимости от вида частного:
столбец № 1 столбец № 2 столбец № 3.
- 10: 5 = 2 10: 4 = 2,5 10: 6 = 1,(6)
- а) 125: 11; б) 273: 70; в) 42 535: 47; г) 1012: 21;
- д) 628: 25; е) 20 600: 2500; ж) 420: 32; з) 88 886: 98;
- и) 91 000: 90; к) 90 000: 36.
- (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 275.)
Следует заметить, что к текстам, способствующим формированию таких когнитивных схем, как инструкции, правила, алгоритмы, относятся тексты, в которых учащимся предлагается выполнить процедуру опознания математических объектов, к которым данный алгоритм или правило могут быть применимы.
Приведем примеры таких текстов в теме «Положительные и отрицательные числа» (6-й класс), где учащимся предлагается провести классификацию математических выражений, значение которых может быть найдено с помощью определенного правила.
Выпишите суммы, в которых слагаемые имеют:
- • одинаковые знаки;
- • разные знаки.
- 1. -26+(-14); 4. -32 + (-28);
- 2. -25 + 17; 5. 107 + (-107);
- 3. -25 + 163; 6. 0 + (-3).
В какой из групп — а) или б) — вы можете только по виду записи определить знак суммы?
Выпишите числовые выражения, в которых для нахождения их значений нужно найти:
- • сумму модулей;
- • разность модулей.
- 1. 13 + 18; 9. 109 + (-82);
- 2. 23+ (-16); 10.35 + 18;
- 3. (-173) + (-2); 11. (-36) + (-78);
- 4. 0 + (-29); 12. -107 + 0;
- 5. 345 + 0; 13. 623 + (-623);
- 6. -23 + 23; 14. 0 + 34;
- 7. 13 — 23 — 16; 15. -12 + 101 — 82.
- 8. -12 + 2;
Найдите значения данных числовых выражений.
(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005, с. 134—135.).
Итак, текст — процедура должен мотивировать поиск алгоритма, создавать условия для выявления его оснований, предъявлять учащимся визуальные средства хранения полученной информации или стимулировать их деятельность по получению соответствующих образов, предлагать задания для освоения процедуры и различных случаев ее использования, включать процедуры опознания тех математических объектов, к которым может быть применим данный алгоритм.
Работа с текстами — процедурами развивает у учащихся умение строить алгоритмы, представлять их разными способами, придерживаться полученных алгоритмов, что является важным качеством математического мышления.
Еще одним типом текста, направленным на формирование когнитивных схем, является «текст — конспект», в рамках которого учащиеся анализируют конспекты, составленные кем-то, а также самостоятельно составляют собственные конспекты.
Такая работа в серии учебных книг МПИ-проекта начинается в теме «Положительные и отрицательные числа» (6-й класс), где учащиеся работают с конспектами одного из персонажей, и продолжается в остальных книгах, меняя свою форму. Это могут быть «грамотки», «записки» и т. п. Приведем фрагмент одного из таких текстов — конспект Мальвины.

(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005, с. 44.).
Таким образом, выделены типы текстов, способствующие созданию когнитивных схем для хранения в памяти видовых и родовых примеров изучаемых понятий, воспроизведению инвариантных и вариативных знаний о математических объектах, построению алгоритмов и правил выполнения математических действий, а также систематизации усвоенного материала. В том числе:
- • текст — введение фокус-примера;
- • текст — фрейм;
- • текст — процедура;
- • текст — конспект.