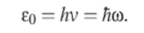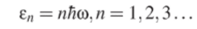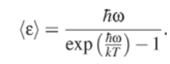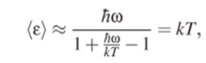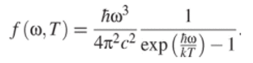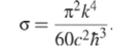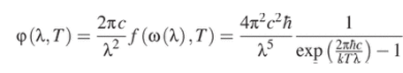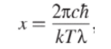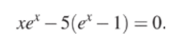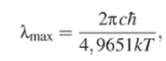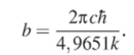Квантовый расчет функции Кирхгофа. 
Формула Планка

Ситуацию спас Планк, предположив, что энергия может излучаться только порциями — квантами. Энергия такого кванта.

Здесь h — так называемая «перечеркнутая** постоянная Планка, равная 10^-34 Дж-с. Соответственно, И — «неперечеркнутая** постоянная Планка, И = 2лТг. Любая порция энергии должна быть кратна энергии кванта так же, как любой электрический заряд должен быть кратен заряду электрона: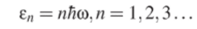

Это сразу меняет среднюю энергию моды.

Переход к классической физике соответствует отказу от дискретизации энергии, т. е. пределу h —? 0. При этом, как легко видеть.

как и в классической термодинамике. С учетом нового выражения для (е) функция Кирхгофа принимает вид.

Последнее выражение называют формулой Планка. График такой функции после перехода от частот к длинам волн (раздел 6.7.3) совпадает с экспериментальной кривой рис. 6.63.

Квантовый расчет энергетической светимости. Теоретическое обоснование законов Стефана — Больцмана и Вина.

И итерируя по частотам функцию Планка, получаем для энергетической.

светимости абсолютно черного тела следующее выражение

Но это в точности соответствует закону Стефана-Больцмана (раздел 6.7.3), причем постоянная Стефана—Больцмана здесь выражена через более фундаментальные постоянные.

Разумеется, подстановка в правую часть численных значений постоянных дает для о значение, близкое к экспериментальному. Самое существенное здесь, однако, то, что величина R* конечна.

Чтобы определить длину волны, на которую приходится максимум излучения в спектре абсолютно черного тела, необходимо перейти в функции Кирхгофа к зависимости от длины волны.

и исследовать ее на экстремум. Решая уравнение dy/dX = 0 и переходя в нем к безразмерной переменной х

получаем для нее трансцендентное уравнение.

Численное решение этого уравнения дает х % 4,9651. Таким образом.

т.е. и здесь теоретически воспроизведен закон Вина, причем постоянная Вина выражена через более фундаментальные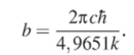

Пирометрия.

Под этим понимают совокупность методов бесконтактного определения температуры. Можно определять температуру, измеряя светимость тела и используя закон Стефана — Больцмана. Такую температуру называют яркостной. Другой способ — определять длину волны, на которую приходится максимум в спектре излучения тела. Если эта длина лежит в оптическом диапазоне, она определяет видимый цвет тела. Поэтому подобную температуру называют цветовой.