Обработка результатов наблюдений и оценка погрешностей измерений

Измерения с однократными наблюдениями

Большинство измерений является однократными. В обычных условиях их точность вполне приемлема. Результат однократного измерения 0 записывается следующим образом:

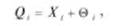
где X, — значение /'-го показания; 6, — поправка.

Необходимым условием проведения однократного измерения служит наличие априорной информации. К ней относится, например, информация о виде закона распределения вероятности показания и мере его рассеивания, полученная из опыта предшествующих измерений. Такой информацией может служить, например, класс точности средства измерения.

Оценку погрешности результата измерения выполняют при разработке методики выполнения измерений. Источниками погрешностей являются модель объекта измерения, метод измерения, средство измерения, оператор, влияющие факторы условий измерений, алгоритм обработки результатов измерений. Как правило, погрешность результата измерения оценивается при доверительной вероятности Р = 0,95.

При выборе доверительной вероятности Р учитывается степень важности результата измерений. Например, если результат измерения связан с безопасностью жизнедеятельности человека, то значение доверительной вероятности Р должно быть увеличено.

За результат измерения в этом случае принимают результат однократного наблюдения л-(с введением поправки, если она имеется), используя предварительно полученные (например, при разработке методики выполнения измерений) данные об источниках, составляющих погрешность.

Доверительные границы неисключенного остатка систематической погрешности результата измерения В (Р) вычисляют по формуле.

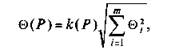
где к (Р) — коэффициент, определяемый принятой Р и числом т составляющих неисключенного остатка систематической погрешности; в, — найденные нестатистическими методами границы /'-й составляющей неисключенного остатка систематической погрешности. При Р = 0,9 к (Р)= 0,95, при Р = 0,95 к (Р)= 1,1 при любом числе слагаемых т. При Р = 0,99 значения к (Р) определяются.

Если составляющие неисключенного остатка систематической погрешности распределены равномерно и заданы доверительными границами &,(Р,), то доверительную границу результата измерения вычисляют по формуле.

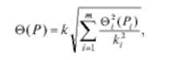
где к и к, — те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности Ри /^соответственно; т — число составляющих неисключенного остатка систематической погрешности.

Среднее квадратичное отклонение результата измерения с однократным наблюдением вычисляют одним из следующих способов:

— если в технической документации на средство измерения или в методике выполнения измерения указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т. д.), то среднее квадратичное отклонение определяют по формуле:

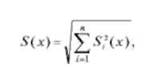
где п — число составляющих случайной погрешности; 5, — значения среднего квадратичного отклонения этих составляющих.

Доверительную границу случайной погрешности результата измерения е (Р) в этом случае вычисляют по формуле.

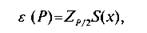
где 2Р/2 — значение нормированной функции Лапласа в точке Р/2, при доверительной вероятности />(0,90 < Р< 0,99) определяется по формуле.

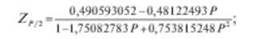
— если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами е (Р) при одной и той же доверительной вероятности Р, то доверительную границу случайной погрешности результата измерения с однократным наблюдением при доверительной вероятности Р вычисляют по формуле.

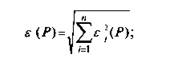
— если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений п (< 30, то.

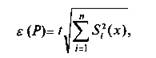
где / - коэффициент Стьюдента, соответствующий наименьшему числу наблюдений п из всех п, 5((х) — оценки средних квадратичных отклонений случайных составляющих погрешности результата наблюдения, определяемых по формуле.

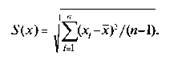
Если в эксперименте невозможно или нецелесообразно определять среднее квадратичное отклонение составляющих случайной по;

грешности, а определено сразу суммарное среднее квадратичное отклонение, то в формуле (7.7) п = 1;

— если случайные составляющие погрешности результата наблюдений представлены доверительными границами e (P,)t соответствующими разным вероятностям Я" то сначала определяют среднее квадратичное отклонение результата измерения с однократным наблюдением по формуле.

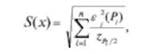
гдегч/2 — значения функции Лапласа. Затем вычисляют е (Р) по формуле (7.4).

Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ.

Если < 0,8, то неисключенным остатком систематической S (x) погрешности В (Р) пренебрегают и окончательно принимают е (Р) за погрешность результата измерения А (Р) при доверительной вероятности Р.

Если ^-^-> 8, то пренебрегают случайной погрешностью и принимают А (Р) = в (Р).

Если 0,8 < < 8, то доверительную границу погрешности результата измерений вычисляют по формуле.

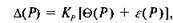
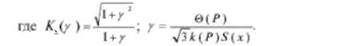
По вычисленному значению находят значения Кх (у).