Модель Самуэльсона — Хикса

В модели Кейнса предполагается, что инвестиции в экономику являются постоянной величиной. Это существенно сужает круг реальных макроэкономических процессов, исследуемых с помощью этой модели. В рассматриваемой модели Самуэльсона — Хикса делается попытка освободиться от данного ограничения и предполагается, что инвестиции состоят из постоянной части /₀ и переменной части, пропорциональной приросту ВВП текущего года по сравнению с прошлым:

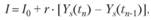
где i — так называемый коэффициент акселерации инвестиций (0 < i < 1). Тогда можно записать уравнение модели Самуэльсона — Хикса, аналогичное уравнению (8.65) модели Кейнса:

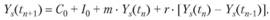(8.70).

С математической точки зрения модель (8.70) представляет собой линейное конечно-разностное уравнение второго порядка с постоянными коэффициентами. Приведем это уравнение к стандартному виду, для чего перейдем по аналогии с предыдущей моделью к относительным безразмерным переменным.

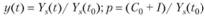
и сдвинем начало отсчета времени на один год назад. Кроме того, для упрощения записи дальнейших преобразований обозначим t_n = п, тогда уравнение (8.70) примет следующий вид:

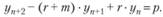(8.71).

Как и в модели Кейнса, решение данного уравнения представляет собой сумму его частного решения и общего решения соответствующего однородного уравнения. Характер общего решения однородного уравнения зависит от дискриминанта этого уравнения.

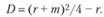
Если D > 0, то колебательных решений нет и объем рынка товаров и услуг монотонно стремится к своему асимптотическому значению, равному стационарному решению уравнения (8.71). Это решение может быть найдено из предположения стационарности (y_n+2 = y_n+1 = y_n):

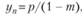(8.72).

что совпадает с соответствующим выводом (8.68) по модели Кейнса.

Если D < 0, то в течение некоторого переходного периода решение имеет колебательный затухающий характер, вследствие чего решение уравнения (8.71) с дальнейшим ростом времени стремится к стационарному значению (8.72).

Как отмечалось, в реальных условиях выполняются ограничения на коэффициент акселерации инвестиций и предельную склонность к потреблению: 0 < r < 1; 0 < т < 1. Поэтому дискриминант однородного уравнения в рассматриваемой модели может принимать как положительные, так и отрицательные значения. Пример численного расчета по модели Самуэльсона — Хикса с использованием средств пакета Excel при значениях параметров r = 0,495; т = 0,636 (D = -0,175) осуществлен и представлен графически в [1, с. 365]. Таким образом, можно сделать вывод о том, что модель Самуэльсона — Хикса в состоянии объяснить наличие колебаний на рынке товаров и услуг.

Модель Солоу

Динамическое равновесие, описываемое в предыдущих классических моделях, было достаточно устойчивым для ранних стадий развития рыночной экономики, когда эти модели неплохо описывали реальные макроэкономические процессы. Для последующих периодов развития кейнсианские модели роста оказались малопригодны ввиду нестабильности динамического равновесия в этих моделях. Р. Солоу показал, что такая нестабильность является следствием отсутствия взаимозаменяемости факторов производства, поскольку в этих моделях вообще не рассматривались трудовые ресурсы. Рассмотрим основные положения макроэкономической модели Солоу.

Модель Солоу является односекторной моделью экономического роста, когда экономическая система рассматривается как единое целое и производит один универсальный продукт. Этот продукт может как потребляться, так и инвестироваться, при этом экспорт и импорт в явном виде не учитываются.

Состояние экономики в модели Солоу задается следующими эндогенными переменными:

Y — валовой внутренний продукт (ВВП);

С — фонд непроизводственного потребления;

I — инвестиции;

L — число занятых в экономике;

К — основные производственные фонды (ОПФ).

Все эндогенные переменные считаются функциями времени; для упрощения записи аргумент времени опущен.

Кроме отмеченных эндогенных переменных, в модели используются также следующие экзогенные параметры:

v — годовой темп прироста числа занятых в экономике (-1 < v < 1);

? — доля выбывших за год основных производственных фондов (0 <? < 1);

? — доля валовых инвестиций в ВВП, или норма накопления (0 <? < 1).

Экзогенные параметры являются управляющими и не зависят от времени.

В модели Солоу предполагается, что годовой выпуск продукции определяется однородной производственной функцией первого порядка Кобба — Дугласа:

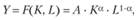(8.73).

где, а — коэффициент эластичности ВВП по основным производственным фондам. Определенная таким образом производственная функция удовлетворяет очевидному равенству.

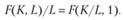(8.74).

Рассмотрим изменения ресурсных показателей за малый промежуток времени At. Согласно определению темпа прироста занятых в экономике.

, или (при 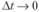) 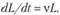(8.75).

Решение дифференциального уравнения (8.75) описывает экспоненциальный рост занятых в экономике:

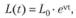(8.76).

где L₀ — заданное начальное число занятых в экономике. Таким образом, в модели Солоу численность занятых в экономике в любой момент времени t является известной величиной.

Износ ОПФ за время ?t равен m · К · ?t, а прирост инвестиций за это же время составляет I · ?t. Поэтому прирост ОПФ за время ?t будет равен.

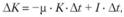
откуда при ?t > 0 можно получить дифференциальное уравнение, описывающее динамику основных производственных фондов:

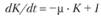при начальном условии К (0) = K_Q. (8.77).

Инвестиции и фонд потребления следующим образом выражаются через ВВП:

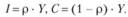(8.78).

Таким образом, полную систему уравнений модели Солоу при условии, что ВВП определяется функцией Кобба — Дугласа, образуют уравнения (8.73), (8.76), (8.77) и (8.78):

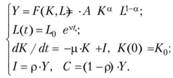(8.79).

Систему уравнений (8.79) можно упростить путем деления всех входящих в нее величин на численность занятых в экономике L, т. е. записать эту систему в расчете на одного занятого (см., например, равенство (8.74)).

Систему уравнений модели Солоу можно решить методом последовательных приближений, используя электронные таблицы Excel. Особый интерес представляет поиск стационарных решений (траекторий) модели Солоу, т. е. таких траекторий, на которых фондовооруженность является постоянной величиной и равна, следовательно, своему начальному значению К(0) = К₀. Для стационарных решений dK/dt = 0, следовательно, на стационарных траекториях выполняются очевидные равенства:

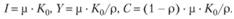(8.80).

Анализ стационарных решений модели Солоу позволяет сделать вывод, что на стационарной траектории все основные макропоказатсли растут по экспоненциальному закону пропорционально трудовым ресурсам L (t).

Если в качестве критерия оптимальности развития экономики принять максимум удельного непроизводственного потребления С/L, то в результате несложных математических выкладок можно получить для оптимальной нормы накопления (доли инвестиций в ВВП) равенство.

?_опт =? (8.81).

Равенство (8.81) выражает тот факт, что оптимальная норма накопления в стационарном режиме для производственной функции Кобба — Дугласа равна коэффициенту эластичности по основным производственным фондам. Этот вывод, полученный в результате анализа стационарных решений модели Солоу, носит название «золотого правила» экономического роста.