Проект 2.3. Перекрестная валидация (скользящий контроль)

Еще один метод валидации использует идею случайного разбиения данных на две части, обучающую и тестовую. Результаты, полученные на обучающем множестве, применяют к тестовому множеству и сравнивают с тем, что известно для тестового множества. Для того чтобы каждый объект попадал в обучающее и тестовое множества с одинаковой частотой, пользуются специально разработанным методом перекрестной валидации, по-русски называемым иногда скользящим контролем.

Так называемая К-частная перекрестная валидация организована следующим образом. Случайным образом разбиваем множество объектов на К частей Q (k) одинакового размера^[1], k = 1, …, К. По традиции, К выбирают равным 2, 5 или 10.

В цикле по k каждая часть Q (k) используется как тестовое множество, а объединение остальных образует обучающее множество. Рассматриваемый метод анализа данных применяют к обучающему множеству (стадия обучения), а результат применяют к тестовой выборке. Средняя оценка, но всем тестовым множествам составляет оценку качества метода по К-частной перекрестной валидации.

Случай, когда К равно числу объектов N, особенно популярен. Ранее он назывался джек-найф (Jack-knife — складной нож), но сейчас чаще пользуются названием «выставлять-по-одному» (leave-one-out). Это название отражает суть метода: проводится Дообучений анализируемого метода на множествах, полученных исключением из X ровно одного объекта.

Применим метод 10-частной перекрестной проверки к задаче оценки математического ожидания вышерассмотренных трех наборов данных short.dat. Для начала разобьем множество из 50 объектов на 10 непсресекающихся классов по пять объектов каждый. Важно, чтобы объекты попадали в классы разбиения случайным образом. Это может быть достигнуто несколькими способами. Например, сначала инициализируются 10 пустых классов. Затем объекты один за другим помещаются в случайно выбираемый класс. Другой способ: случайно перемешиваем все индексы объектов и разделяем перемешанное на 10 частей, в каждой по пять объектов. Для каждого класса Q (k) (k = 1, 2, …, 10), находим среднее значение и стандартное отклонение на всех остальных 45 объектах. Найденные 10 средних и стандартных отклонений усредняются.

Результаты представлены в табл. 2.8. Показатели, рассчитанные для исходного распределения и с использованием 10-частной перекрестной валидации, схожи. Означает ли это, что в использовании этого метода нет надобности? В данном случае — возможно, но когда речь идет о доверии к результатам более сложных методов анализа данных, результаты могут различаться существенным образом. Кроме того, отметим, что квадратичные отклонения на десяти тестовых множествах для Гауссова и двумодального распределения близки друг к другу, а для степенного закона — сильно различаются и варьируют от 391,60 до 2471,03.

Рис. 2.15. Размах [2, 12], разделенный на пять бинов

Квадратичные отклонения от математического ожидания, построенные для исходного множества и с использованием 10-частной перекрестной валидации

Таблица 2.8

Вопрос 2.9. Каков размер бина на рис. 2.15?

Ответ. Равен 2.

Вопрос 2.10. Рассмотрим признак х, изменяющийся в пределах между 1 и 10. Разделим размах х на 9 бинов (в этом случае длина бина — 1). Частоты х в бинах в порядке нумерации равны: 10, 20, 10, 20, 30, 20, 40, 20, 30. Ответьте на вопросы:

• (i) Сколько всего наблюдений х?
• (ii) Что можно сказать о медиане х?
• (iii) Посчитайте минимальную и максимальную оценки среднего значения х.
• (iv) Что можно сказать о 20%-ных квантилях х?
• (v) Как выглядит распределение х, если число бинов равно 3? Какова качественная дисперсия (индекс Джини) для этого распределения?

Ответы.

• (i) Всего 200 наблюдений.
• (ii) Медиана лежит между 100-м и 101-м значением в упорядоченном списке, т. е. в шестом бине, следовательно, между 6 и 7.
• (iii) Минимальная оценка математического ожидания рассчитывается по минимальным значениям признака в бинах: (1 • 10 + 2−20 + 3- 10 + 4−20 + 5−30 + + 6 • 20 + 7 • 40 + 8 • 20 + 9 • 30) / 200 = 5,7.

Максимальная оценка рассчитывается по той же формуле, только значения признака во всех бинах увеличиваете на 1. Получаем: 5,7 + 1 = 6,7.

• (iv) 20% от 200 равно 40. Это означает, что 20%-ный квантиль с левого края — это 4,20%-ный квантиль с правого конца попадает в восьмой бин, следовательно, лежит между 8 и 9.
• (v) Данное распределение для случая трех бинов будет 40, 70, 90 или, в относительных частотах, 0,2, 0,35, 0,45. Следовательно, индекс Джини равен 1 — 0,2² — - 0,35²— 0,45² = 0,635.

Вопрос 2.11. Центральные значения. Из 100 покупателей новогодних подарков 50 потратили по 60 долл., 20 потратили по 100 долл., и 30 — по 150 долл, каждый. Найдите (i) среднюю, (ii) медианную и (iii) модальную траты. Подсказка: Как, учитывая то, что покупатели объединены в три группы, сделать вычисления центров более эффективными?

Ответы.

Среднее. Для начала найдем доли покупателей, потративших по 60, 100 и 150 долл, каждый. Получим 0,5, 0,2 и 0,3 соответственно. Среднее может быть вычислено так: сложим все затраты, взвесив их соответствующими пропорциями. Получим: с = 60 • 0,5 + 100 0,2 + 150 — 0,3 = 30,0 + 20,0 + 45,0 = 95.

Медиана. Согласно определению медиана 100 чисел — это значение посредине между 50-м и 51-м объектом в отсортированном списке. В нашем случае на этих местах стоят 60 и 100, поэтому медиана затрат — 80 долл.

Мода. Модальное значение — наиболее вероятное, т. е. 60.

Вопрос 2.12. Рассмотрим два геологических разреза, для одного из которых имеется семь образцов, а для другого — пять. Содержание определенного минерала в образцах разреза А описано вектором а = (7,6; 11,1; 6,8; 9,8; 4,9; 6,1; 15,1), а в разрезе В — b = (4,7; 6,4; 4,1; 3,7; 3,9). Среднее содержание этого минерала в А составляет 8,77, а в В — 4,56. Протестируйте гипотезу «содержание минерала в разрезе А больше, чем в разрезе В» на 95%-ном уровне доверия с использованием бутстрэпа.

Ответ. Поскольку множества маленькие, число испытаний должно быть выбрано не слишком большим. При 200 испытаниях 95%-ный доверительный интервал образован 6-м и 195-м значениями в списке отсортированных средних значений бутстрэпа. В нашем случае это интервал (6,66, 11,09) для А и (3,82, 5,44) для В. Поскольку все элементы первого интервала больше всех элементов второго, гипотеза может считаться подтвержденной. (Данное решение не совсем корректно, так как в утверждении «разрез А богаче разреза В» есть неточность. Например, можно считать, что А богаче В на 95%-ном уровне доверия, если случайная выборка из А богаче случайной выборки из В в 95% случаев. Тогда 95%-пого интервала не достаточно, поскольку он покрывает только 0,95 • 0,95 = = 90,25% всех возможных пар средних значений бутстрапа.) Посмотрим на минимальные и максимальные средние значения бутстрапа. Размах средних значений равен (6,33, 11,94) для А и (3,82, 5,82) для В. Интервалы не пересекаются, один лежит строго правее другого, что означает, что гипотеза доказана, даже и при ограничениях метода.

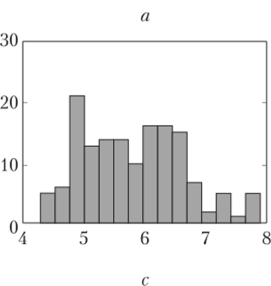
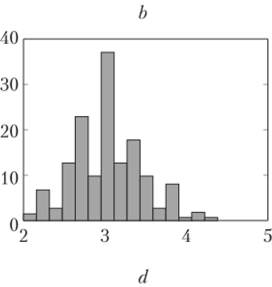
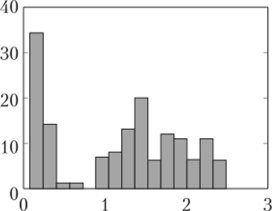
Рис. 2.16. Гистограммы всех четырех признаков в данных «Ирисы»:

с и d явно бимодальны Вопрос 2.13. Распределения признаков в данных об ирисах. Рассмотрите гистограммы признаков из данных об ирисах и покажите, что два признака бимодальны.

Ответ. Используем команду МатЛаба.

" for k=l:4;subplot (2,2,k);hist (iris (, k), 15);end; % 15 здесь — задаваемое число бинов и получим рисунок типа рис. 2.16. Очевидно, что третий и четвертый признаки бимодальны.

Вопрос 2.14. Студент решил провести вычислительный эксперимент. Он случайным образом сгенерировал относительные частоты категорий для качественного признака с тремя категориями. Для этого он сгенерировал три случайных числа в интервале (0, 1) и затем нормировал их общей суммой трех чисел, чтобы в результате получить сумму 1. Если, например, сгенерированы 0,7116, 0,1295, 0,6598, то после деления на их сумму 1,5009 получатся величины 0,4741, 0,0863, 0,4396, дающие в сумме 1. Правильны ли действия студента?

Ответ. Нет, не совсем, поскольку создается сдвиг в сторону равных частот. На рис. 2.17, а представлено распределение первой из пары частот, найдснных описанным методом: два случайно сгенерированных числа делятся на их сумму. Распределение далеко от равномерного распределения, представленного на рис. 2.17, Ь. (Можете объяснить разницу?).

Правильным был бы, например, следующий метод генерации случайной тройки чисел. Сначала генерируем два случайных числа; сортируем их по возрастанию. Добавим 0 и 1 к выборке: г₀ = 0 < г_{ < г₂< г₃ = . Затем определим искомые частоты как разности между соседними элементами, p_k = r_k — r_{k {} (k = 1, 2, 3). Например, если сначала были сгенерированы величины 0,8775 и 0,5658, искомые частоты будут определены как р_х = 0,5658, р₂ = 0,8775 — 0,5658 = 0,3117, и р₃ =1 — 0,8775 = = 0,1225. При этом все получаемые частоты так же равномерно распределены, как и исходные две. Этот метод легко распространить на любое числа категорий.

Рис. 2.17. Гистограммы выборок из 10 000 элементов:

а — первый элемент из случайной пары после деления на сумму двух величин; b — равномерная случайная величина.

Кстати говоря

• 2.1. Распределение признака
• 2.1.1. Мальчик сидит со своим отцом за столом, прорабатывая уроки по изучению общественных отношений. Когда они приступают к главе об управлении страной, мальчик спрашивает:
  • — Пап, а сколько людей работает в правительстве США?

Отец без малейшего колебания отвечает:

• — Примерно половина из них.
• 2.1.2. Всероссийское радио начинает передачи и сообщает:
  • — В Москве — 15 часов, в Свердловске — 16, в Томске — 17, в Иркутске — 18, во Владивостоке — 23, в Петроиавловске-Камчатском — полночь.

Человек слушает, слушает и говорит:

• — Ну и бардак в стране!
• 2.1.3. На вопрос «Пользуетесь ли вы Интернетом?» утвердительно ответили 100% россиян. Таков результат опроса, проведенного недавно в Интернете.
• 2.1.4.
• — Знаете ли Вы, что по статистике каждый двухсотый мужчина имеет рост выше двух метров?
• — Еще бы мне не знать! Он каждый раз сидит передо мной в кинотеатре.

• [1] Это можно сделать, начав с пустых множеств Q (k), повторно в цикле по k = 1 / К случайновыбирая из множества объект (без возвращения) и помещая его в Q (k) процесс заканчивается, когдане остается нераспределенных объектов.