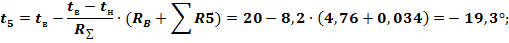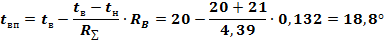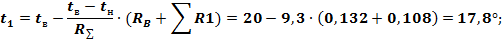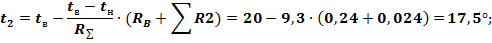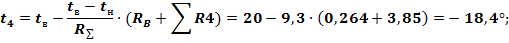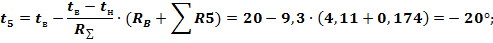Случай апериодического движения (n > k)

Если (случай большого сопротивления среды), то корни характеристического уравнения (17) являются действительными и отрицательными. решение уравнения (16) в этом случае имеет вид:

.

Взяв производную по времени от (21) и использовав начальные условия, можно определить постоянные интегрирования С1 и С2.

Сценарии развития событий в этом случае показаны на рис. 8.

Из графиков видно, что движение точки в этом случае носит не колебательный характер и точка с течением времени асимптотически приближается к положению равновесия: .

При этом кривая — 1 соответствует случаю, когда; кривая 2 соответствует случаю, когда; кривая 3 соответствует случаю, когда. Во всех трех примерах принято, что x0 > 0.

Случай апериодического движения (n = k)

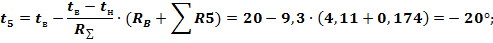
Если (это также случай большого сопротивления среды), то корень характеристического уравнения (17), то есть является кратным, действительным и отрицательным. решение уравнения (16) в этом случае имеет вид:

.

Взяв производную по времени от (22) и использовав начальные условия, можно определить постоянные интегрирования С1 и С2. В этом случае, найдя предел по правилу Лопиталя, получим.

.

Следовательно, и в этом случае движение точки носит неколебательный характер, и точка с течением времени асимптотически приближается к положению равновесия. Сценарии развития событий в этом случае такие же, как и на рис. 8.