Иллюстрация принципа наглядности

Матрицы, ступенчатые матрицы, приведение матрицы к ступенчатому виду — вещи конструктивные и сами по себе наглядные.

Метод Гаусса, или метод последовательного исключения неизвестных, является универсальным практическим методом решения произвольных систем линейных уравнений (СЛУ). По своему значению и эффективности его можно сравнить разве только со знаменитым алгоритмом Евклида — методом нахождения НОД для целых чисел и многочленов. Будем рассматривать СЛУ и матрицы с действительными коэффициентами. Суть метода Гаусса заключается в приведении произвольной матрицы к ступенчатому виду при помощи элементарных преобразований ее строк:

• 1) прибавление к некоторой строке любой другой;
• 2) умножение любой строки на действительное число, отличное от нуля;
• 3) вычеркивание или приписывание нулевой строки.

Заметим, что при помощи первого и второго преобразований, примененных несколько раз, можно переставить строки. Скажем, надо поменять местами строки А₍ и А_;. Прибавим к i-й строке ;-ю:

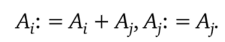
Прибавим к;-й строке i-ю строку, умноженную на -1:

Прибавим к i-й строке j-ю и умножим j-ю строку на -1:

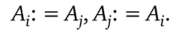
Наряду с элементарными преобразованиями строк можно использовать элементарные преобразования столбцов. Будем пользоваться теми и другими преобразованиями, как удобнее.

Сначала отметим широкое практическое применение метода Гаусса. Во-первых, это универсальный метод решения систем линейных уравнений — метод исключения неизвестных. Здесь к ступенчатому виду приводится расширенная матрица СЛУ. Во-вторых, способ нахождения ранга матрицы или системы векторов (приводим матрицу к ступенчатому виду, сколько останется строк — таков ранг матрицы). Кроме того, метод Гаусса можно использовать при нахождении обратной матрицы. Можно рассматривать его как способ вычисления определителей (сведением к треугольному виду).

Помимо широкого практического применения метод Гаусса с успехом может быть применен при доказательстве многих теорем линейной алгебры.

Сначала обосновывается, что элементарные преобразования над уравнениями системы линейных уравнений приводят к эквивалентной системе, т. е. не меняют множества ее решений. Далее показывается, что любую систему линейных уравнений с помощью конечного числа линейных преобразований можно привести к ступенчатому виду. И мы можем проводить анализ системы линейных уравнений: является ли система совместной или несовместной, определенной или неопределенной.

Как следствие, доказывается:

Теорема 1 (о существовании ненулевых решений однородной

СЛУ). Однородная система линейных уравнений, в которой число неизвестных больше числа уравнений, имеет ненулевое решение.

Доказательство. Приводим систему линейных уравнений к ступенчатому виду при помощи элементарных преобразований. При этом мы не могли получить уравнение вида:

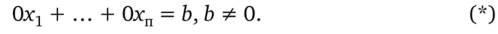
Хотя, возможно, мы получали нулевые уравнения. Поэтому число уравнений в ступенчатой СЛУ меньше либо равно числу уравнений изначальной СЛУ. А, значит, в ступенчатой СЛУ число уравнений меньше числа неизвестных. Выражая свободные неизвестные через главные, убеждаемся, что СЛУ имеет бесконечно много ненулевых решений.

Вводим понятия строчечного (и столбцового) ранга матрицы как максимального числа линейно независимых строк (столбцов), рассматриваемых как векторы.

Легко проверяется, что линейные преобразования над строками и столбцами не меняют ни строчечный, ни столбцовый ранг матрицы. После чего «наглядно» доказывается (сравните это доказательство с приведенным выше более абстрактным доказательством).

Доказательство. Приведем матрицу к ступенчатому виду. Строчечный ранг матрицы равен числу ненулевых строк, скажем г. Столбцы можно рассматривать как r-мерные вектора, а потому столбцовый ранг не превосходит г — строчечный ранг. Транспонируем матрицу. Для нее столбцовый ранг также не превышает строчечный. Значит, столбцовый и строчечные ранги равны.

Теорема 3 (Кронекера—Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу расширенной матрицы.

Доказательство. Необходимость. Приведем расширенную матрицу системы к ступенчатому виду. Так как СЛУ совместна, то мы не можем получить уравнения типа (*). Следовательно, число (ненулевых) строк в полученных ступенчатых расширенной матрице и основной матрице системы одно и то же.

Достаточность. Приведем расширенную матрицу системы к ступенчатому виду. Так как ранги основной и расширенной матриц системы равны, то число ненулевых строк в основной матрице равно числу строк в расширенной матрице системы. Следовательно, у нас нет уравнения типа (*), значит, СЛУ совместна.

Теорема 4. Если система линейных уравнений совместна, то данное уравнение от этих же неизвестных является ее следствием тогда и только тогда, когда оно представимо в виде линейной комбинации уравнений системы.

Доказательство. Необходимость. Приписав новое уравнение к рассматриваемой совместной системе т линейных уравнений, имеющей ранг г, получим равносильную систему из т + 1 уравнения. Приведем полученную систему к ступенчатой системе. Первые ее г уравнений получаются из уравнений начальной СЛУ, а последнее уравнение окажется нулевым. Но это нулевое уравнение получается (в конце концов) прибавлением к новому уравнению некоторой линейной комбинации m исходных уравнений. Обратная импликация очевидна.

Теорема 5 (о фундаментальной системе решений). Если ранг г основной матрицы однородной СЛУ меньше числа ее переменных п, то СЛУ имеет фундаментальную систему решений, состоящую из п — г решений.

Доказательство. Приведем СЛУ к ступенчатому виду. Получим г ненулевых строк. Будем придавать свободным неизвестным поочередно значение 1, а остальным — 0. Получим матрицу решений из п — г строк. Строки линейно независимы, и любое другое решение СЛУ является линейной комбинацией этих решений.

Теорема 6. Квадратная матрица является невырожденной тогда и только тогда, когда ее строки (столбцы) линейно независимы.

Доказательство. Пусть дана квадратная матрица порядка т. С помощью элементарных преобразований строк она приводится к треугольному виду. Элементарные преобразования сохраняют как ранг, так и невырожденность матрицы. Остается заметить, что определитель треугольной матрицы равен произведению ее диагональных элементов.

Теорема 7 (о ранге матрицы). Ранг матрицы равен максимальному порядку ее миноров, отличных от нуля.

Доказательство. Рассмотрим частный случай, когда все т строк матрицы Л линейно независимы. Приводим матрицу Л к ступенчатому виду с помощью элементарных преобразований типа 1 и 2. Затем переставляем столбцы так, чтобы получилась трапецеидальная матрица.

В. При этом ранг матрицы не меняется. Беря в матрице В первые т столбцов, получаем невырожденную треугольную матрицу порядка т.

Пусть теперь А — произвольная матрица иг — максимальный порядок ее ненулевого минора. Можно считать, что этот минор расположен в г первых строках матрицы, которые необходимо будут линейно независимыми по теореме 6. Остальные строки матрицы А являются линейными комбинациями первых г строк. Если это не так, добавим к г первым строкам еще одну строку матрицы, не являющуюся их линейной комбинацией. Тогда (по первому случаю) найдется минор порядка г + 1, отличный от нуля, что невозможно.

В заключение заметим, что все сказанное справедливо для конечномерных векторных пространств и СЛУ над произвольным полем Р вместо R. Линейная алгебра излагается в известных учебниках А. И. Мальцева, И. М. Гельфанда, А. И. Кострикина, Л. Я. Куликова, А. В. Архангельского, С. Ленга, Г. Стренга и других.

И. Изложение темы «Определители». Хорошо известны три определения понятия определителя числовой квадратной матрицы: обычное (сумма произведений элементов матрицы по подстановкам индексов), индуктивное (через разложение по строке или столбцу) и аксиоматическое (как знакопеременная полилинейная функция столбцов или строк). Каждое из них имеет свои преимущества и недостатки. Классическое определение определителя п-го порядка конструктивно, позволяет легко доказать исходные свойства определителей, но при п > 4 малопригодно для вычислений. Индуктивное определение также конструктивно, более эффективно для вычислений, но при таком подходе усложняются доказательства основных свойств. Наконец, аксиоматическое определение не конструктивно, требует доказательства теоремы существования и единственности, но хорошо работает при выведении ряда общих свойств определителей.

Можно предложить следующую схему изучения определителей.

• 1. Традиционное введение определителей.
• 2. Доказательства по определению нескольких простейших свойств определителей и разложения определителя по строке.
• 3. Формальное выведение из этих свойств других основных свойств определителей.
• 4. Общая лемма и теорема об определителе произведения матриц.
• 5. Эквивалентность обычного, индуктивного и аксиоматического определений.
• 6. Приложение определителей: правило Крамера, условия обратимости матрицы, формула для обратной матрицы.

Рассмотрим подробнее реализацию данной схемы.

Определители естественным образом возникают при решении систем линейных уравнений с числовыми коэффициентами методом последовательного исключения неизвестных. При решении систем линейных уравнений с двумя и с тремя неизвестными появляются определители второго и третьего порядка. При этом получаются разложение определителя третьего порядка по строке и правило Крамера. Определитель третьего порядка определяется стандартно как выражение (число) от своих элементов, записываемое (вычисляемое) с помощью простого мнемонического правила. Здесь, как в зародыше, заложена вся стройная теория определителей.

Напомним классическое определение. Пусть А = (а^) — произвольная квадратная матрица п-го порядка с действительными коэффициентами a_tj. (Вместо поля R действительных чисел может быть взято любое поле.) Определителем матрицы А называется число D (A), равное сумме п всевозможных произведений а.цa_2i2 элементов матрицы А,

взятых по одному из каждой ее строки и каждого столбца, со знаками s (ос) перестановок их индексов а = (i_v i_n):

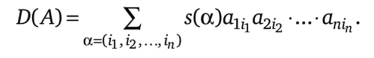
Такой определитель называется определителем п-го порядка. При фиксированном натуральном п определитель п-го порядка удобно считать матричным отображениемD: M"® —" Rpuih функцией П (Л₁₅…, А_п) от п п-мерных столбцов.

На основе определения непосредственно доказываются следующие исходные свойства определителей.

1. D (A_t) = D (A), т. е. определитель транспонированной матрицы равен определителю самой матрицы.

• 2. D (A_1}…, гА_к…, АД — rD (Ai,…, A_i}…, A_n).
• 3. D (A_b…, A_t + B_i3…, АД = D (A_1}…, A_i}…, АД + D (AВ_к…, A_n).
• 4. D (A_V…, A_ir., A,._vA_n) = 0.
• 5. Определитель треугольной матрицы равен произведению ее диагональных элементов, в частности D (E) = 1.

Теорема 1. Для любой квадратной матрицы А = (аД п-го порядка имеет место разложение ее определителя по i-й строке:

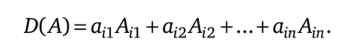
Из свойств 1—5 легко выводятся дальнейшие свойства определителей.

• 6. D (A_b…, A_j}…, A_i}…, А_п) = -D (A_1}…, А_{,…, Ар…, АД при i < j.
• 1. D (A_1}…, A_t + rAp…, АД = D (A_1}…, A_t,…, АД npuj * i.

m m

8. D (A₁,…, ^r_kB_k,…, A_n) = ^_lr_kD (A₁,…, B_k,…, АД.

k=1 k=1

• 9. Если столбцы (строки) квадратной матрицы линейно зависимы, то ее определитель равен нулю.
• 10. Правило вычисления определителей: с учетом свойств 6 и 7 определитель приводится к треугольному виду и применяется свойство 5.

Свойство 1 позволяет в сформулированных выше утверждениях говорить о строках матрицы вместо столбцов.

Теперь мы приведем одну абстрактную лемму, которую применим к доказательству двух важных теорем. В этом месте мы придерживаемся общего подхода Ленга к теории определителей [308, глава XIII, § 4]. Полностью же подобное изложение методически неприемлемо для первоначального изучения средними студентами. Однако использование в преподавании отдельных приемов доказательства свойств определителей из [308] вполне оправданно.

Лемма. Пусть даны матрица, А = (аД п-го порядка и п-мерные столбцы В_ь…, В_п. Положим Q = а_пВ_г +… + a_inB_n для i = 1,…, п. Тогда

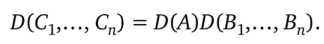
Доказательство. Имеем.

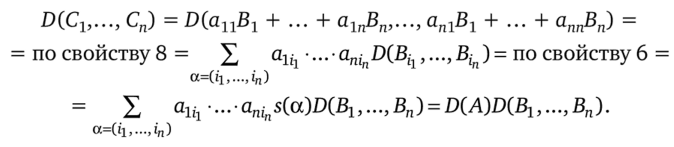
Теорема 2. D (AB) = D (A)D (B) для любых двух квадратных матриц п-го порядка, А и В.

Доказательство. Возьмем матрицу АВ и единичные п-мерные столбцы Е_г =(1, 0, …, 0)^f, Е₂ = (0,1,…, О У,…, Е_п=( 0, .0,…, l)^f. Положим.

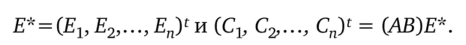
Тогда по лемме.

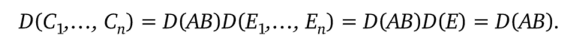
С другой стороны, учитывая формальную ассоциативность (АВ) Е*=А{ВЕ*) и дважды применяя лемму, получаем.

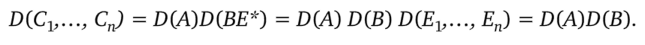
Далее покажем, что три данные выше определения определителя равносильны. Из теоремы 1 следует эквивалентность обычного и индуктивного определений. Свойства 2—5 означают, что определитель гс-го порядка D является знакопеременной полилинейной функций от п п-мерных столбцов, причем D (E_b…, Е_п) = 1.

Теорема 3. Любая знакопеременная полилинейная функция F от п п-мерных столбцов, для которой F (_E_b…, Е_п) = 1, совпадает с D.

Доказательство. Поскольку в доказательстве леммы используются лишь свойства 6 и 8 определителя D, вытекающие из свойств 2—4, то имеем.

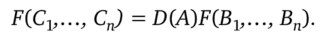
Пусть А_а,…, А_п — произвольные n-мерные столбцы и А = (A₁…A_n)^t. В качестве В, возьмем единичные п-мерные столбцы Е_{ (i = 1,…, п). Тогда.

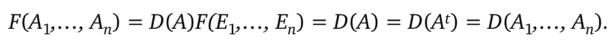
Тем самым получаем абстрактную характеризацию понятия определителя, означающую, в частности, уникальность этого математического объекта.

Рассмотрим, наконец, некоторые важнейшие применения определителей. Следующие теоремы 4—6 доказываются только на основе свойств определителей и теорем 1 и 2.

Теорема 4 (правило Крамера). Пусть система п линейных уравнений с п неизвестными записана в матричной форме АХ=В, и (с_а,___, с_п) —.

решение этой системы. Тогда для каждого i — 1,…, п справедливо равенство С; х D(А) = D (A0, где матрица А¹ получена из матрицы, А заменой i-го столбца столбцом В ceo6odHbLX членов. Поэтому в случае D (A) Ф 0 единственное решение системы АХ = В вычисляется по формуле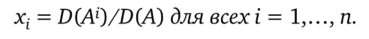

Теорема 5 (критерии вырожденности матрицы). Для любой квадратной матрицы, А равносильны следующие условия:

• 1) Л — вырожденная матрица, т. е. D (A) = 0;
• 2) матрица, А необратима;
• 3) строки (и/или столбцы) матрицы, А линейно зависимы.

По закону контрапозиции получаем необходимые и достаточные условия невырожденности произвольной квадратной матрицы.

Теорема 6 (формула для обратной матрицы). Для любой невырожденной квадратной матрицы А=(а^ п-го порядка

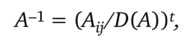
где A₍j — алгебраическое дополнение элемента ау матрицы Л.