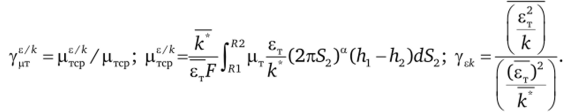Осреднение уравнений движения по сечению канала

Осреднение левой части обобщенного уравнения

Пусть канал, в котором течет газовая смесь, ограничен двумя поверхностями вращения с радиусами RjCSj, t), R₂(S_b t), причем R₂(S_1; О > > Ri (S_1} t) > 0. Для осреднения по сечению канала уравнений (4.1), (4.3), (4.4), (4.5), (4.6), домножим уравнение (4.10) на (2nS₂)" и проинтегрируем по S₂ в пределах otR] до R₂. Воспользовавшись известной теоремой о дифференцировании интеграла по параметру [237], получим осредненное обобщенное уравнение переноса в газовой смеси.

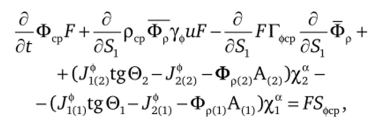
где.

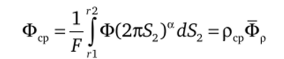
— среднее по сечению значение;

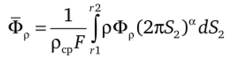
— среднемассовое значение Ф_р;

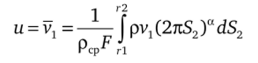
— среднемассовая скорость.

Здесь и далее индекс «ср» означает среднее по площади сечения значение переменной, а черта сверху — среднемассовое, то есть осредненное по площади с весом, равным плотности, и отнесенное к средней плотности значение переменной. При этом.

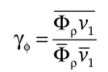
есть коэффициент неравномерности профиля Ф_р в сечении канала. В частности.

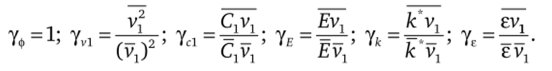
Среднее значение коэффициента переноса Г_фср определяется как отношение среднего по сечению значения продольного потока Ф_р к продольной производной среднемассового значения Ф_р

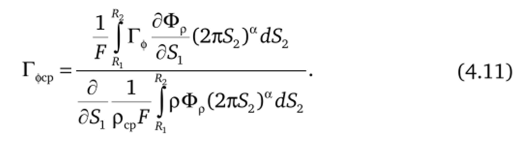
6Ф_Р

= -Гф—^L — поток ф_р в направлении S" i = 1, 2.

dSj

Индексы (1), (2) означают, что параметр вычисляется на поверхности канала с радиусом R_: или R₂ соответственно. Углы 0_Ъ 0₂ есть углы между касательной к образующей боковой поверхности канала и осью Si; Xi — периметр поверхности радиусом Я,;

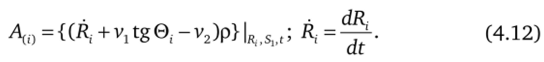
Величины 5_фСр выписаны ниже для каждого уравнения в отдельности.

Особенности, возникающие при осреднении уравнений

При осреднении уравнения движения полагаем, что значения давления на стенках канала мало отличаются от среднего давления в сечении. В этом случае для канала с непроницаемыми твердыми стенками, на которых выполняются условия прилипания, осредненное уравнение движения запишется в виде.

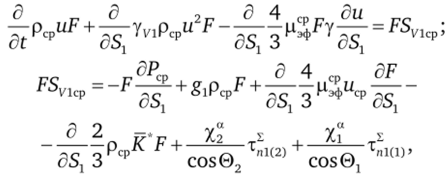
где у = V_lcp/и; Tn_1(i) — проекции напряжений трения на поверхностях R_t канала на продольную ось S_x.

При осреднении по сечению источникового члена уравнения диффузии S_C1 (см. табл. 4.1) введем в рассмотрение средний по отношению к потоку бародиффузии коэффициент бинарной диффузии.

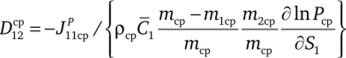
и средний коэффициент термодиффузии.

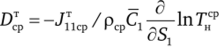
где Т_н^ср — среднекалометрическая температура. Тогда в канале переменной площади с непроницаемыми стенками правая часть осредненного уравнения диффузии запишется.

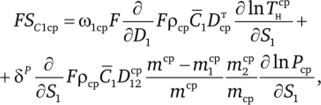
где 6^Р = 1, если бародиффузия учитывается, и б^р = 0 в противном случае.

Осреднение по сечению правой части уравнения энергии проведем при следующих допущениях.

• 1. Предполагаем, что на стенках канала выполняются условия прилипания и существует ламинарный подслой, так что поток диффузии кинетической энергии на стенке в направлении нормали к стенке равен нулю J"() = 0.
• 2. Полагаем, что среднемассовая поперечная скорость много меньше среднемассовой продольной, так что (Ti₂v₂)_{cp cp}, и соответствующим членом диссипативной функции можно пренебречь.
• 3. Полагаем, что распределением давления поперек канала можно пренебречь и считать давление на стенках к — 1, 2 равным среднему Рк ⁼ Рср-

В этих условиях правая часть осредненного уравнения энергии в канале с непроницаемыми стенками запишется.

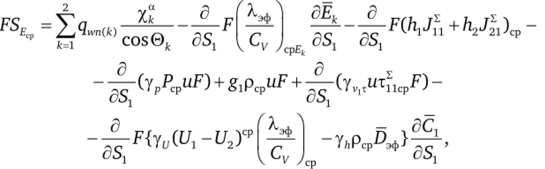
Х^СР где q_lvnm = -^Nu_k(T_wk-T'_p), T'_p=T_cp + ru²/2С_Рср —тепловой поток от стен;

ки к в газ; d₃ — эффективный диаметр канала; г — коэффициент восстановления температуры; Т_ср — среднекалориметрическая температура в сечении; T_wk — температура стенки к в сечении; Е_к — среднемассовое значение кинетической энергии;

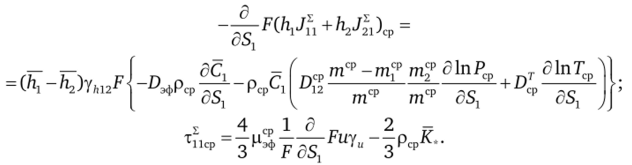
Фигурирующие в (4.13) коэффициенты у_р, y_vlT, y_u, y_ft, у_Л12 определяются следующим образом:

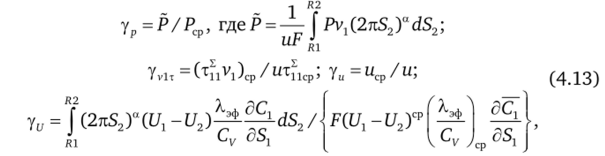
где (L7j — и₂)^ср — среднее значение разности внутренних энергий компонент, сосчитанное по среднекалориметрической температуре;

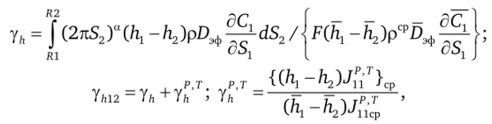
где — поток массы за счет термо-и бародиффузии.

Осреднение правой части S_k уравнения (4.5) баланса кинетической энергии турбулентности (см. табл. 4.1) связано с осреднением по сечению канала произведений производных скорости и может быть корректно проведено лишь с помощью введения большого числа разнообразных коэффициентов неравномерности профилей Vj и v₂, либо с использованием дополнительных предположений о структуре течения. И то и другое делает нецелесообразным использование уравнений к—е модели турбулентности в общем случае при построении квазиодномерных моделей течений в каналах.

В задачах, основным содержанием которых является корректное описание турбулентного перемешивания на контактном разрыве в ядре потока в течение достаточно короткого периода существования контактного разрыва, можно сделать следующие допущения. Ввиду кратковременности процесса (например, процесса выстрела) пограничный слой на стенках канала остается тонким, так что генерация и диссипация турбулентности в пограничном слое и в ядре потока не связаны между собой. Турбулентность в ядре потока обусловлена турбулизацией потока газа на входе в канал (например, генерацией турбулентных пульсаций на поверхности горения пористого заряда торцевого горения) и дальнейшим развитием турбулентных пульсаций в процессе одномерного, или близкого к одномерному, течения в ядре потока. При этом турбулентность в ядре потока можно считать изотропной, причем.

Тогда слагаемое, задающее генерацию кинетической энергии турбулентности в правой части (4.5), запишется.

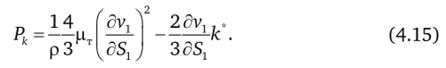
С использованием представления (4.15), правая часть Sуравнения баланса кинетической энергии турбулентности после осреднения запишется.

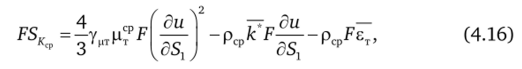
где Уц_Т Цтср/Цср> Мтср Рср^'п ^ Мер определяется по (4.11).

Осреднение уравнения (4.6) баланса диссипации турбулентности проводится по общей схеме При этом правую часть уравнения (4.6) записываем при тех же допущениях, что и в уравнении (4.5), то есть с учетом выражения (4.15). При этом.

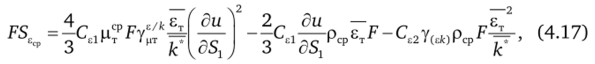
где.