Рассроченные взносы. 
Срок уплаты взносов меньше срока страхования

Вариант немного более сложен, чем предыдущий. За счет наличия в договоре страхования двух временных интервалов с разными финансовыми потоками (период уплаты взносов и временной отрезок после него) резерв «распадается» на две формулы, соответствующие каждому из периодов.

Рассмотрим принципы формирования резерва в период уплаты взносов. Для нашего примера примем период уплаты взносов равным 5 годам и выберем для расчета резерва момент t = 3. Изобразим договор страхования на рис. 2.12.

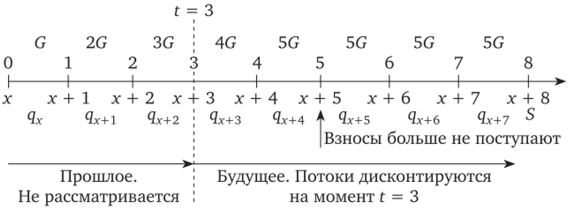
Рис. 2.12. Финансовые потоки страховых выплат для договора с рассроченными взносами. Срок уплаты взносов меньше срока страхования. Этап уплаты взносов.

На рис. 2.12 видно, что первые пять лет выплата по смерти возрастает, а далее стабилизируется на количестве уплаченных взносов. Таким образом, используя логические выкладки предыдущего варианта договора страхования, находим для выплат по смерти: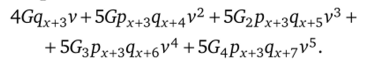

Разобьем данное выражение на две части:

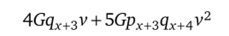
— выплата по смерти возрастает и.

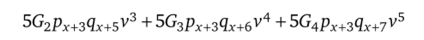
— выплата по смерти постоянна. Рассмотрим каждую часть в отдельности.

Первая часть, 4Gq_x+3v + 5Gp_x+3q_x+4v². Применим такой же подход, как и в версии программы страхования с полным периодом уплаты взносов: разделим каждое слагаемое на два слагаемых, а затем все выражение — на две части:

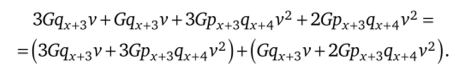
Свернем полученные выражения в уже известные формулы:

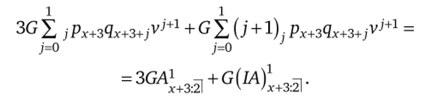
Вторая часть, 5G₂p_x+3q_x+5v³ + 5G₃p_x+3q_x+6v⁴ + 5G₄p_x+3q_x+7v⁵. Здесь, воспользовавшись свойствами вероятности.

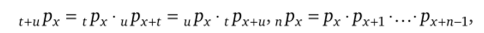
где х, t, и, пе N, вынесем за скобки множитель 5G₂p_x+3v²: 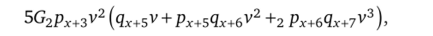что преобразуется в.

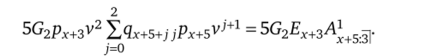
Таким образом, выплата по смерти для данного примера будет выражаться как.

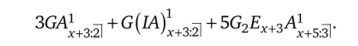
Представим общий вид: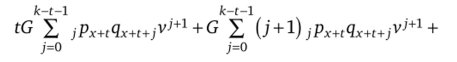

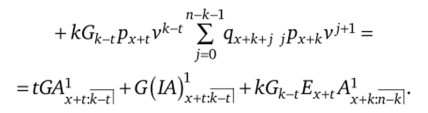
Выплаты по дожитию, как и в предыдущих примерах, SsPx₊3V⁵=S₅E_x+3, их общий вид: S_n__tE_x+t.

Рассмотрим ОСС взносов. На рис. 2.13 представлена схема поступления взносов. Она почти такая же, как и в предыдущем примере. Разница заключается в том, что здесь взносы уплачиваются не весь срок страхования, а его часть (5 лет). Это необходимо учитывать при формировании резерва.

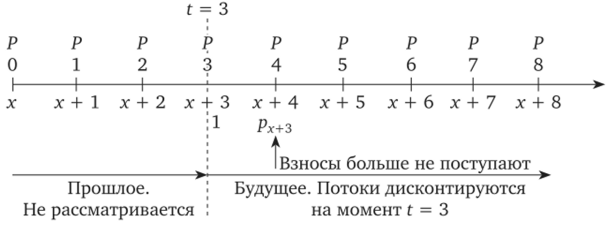
Рис. 2.13. Финансовые потоки страховых взносов для договора с рассроченными взносами. Срок уплаты взносов меньше срока.

страхования На схеме видно, что для момента t = 3 остается два взноса, которые должен уплатить клиент. Один взнос непосредственно в момент t = 3, другой — через год:

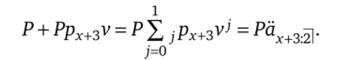
В общем виде:

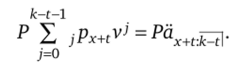
Итак, найдены все составляющие для формулы резерва: ОСС выплат по смерти, ОСС выплат по дожитию, ОСС взносов. Собираем резерв для рассматриваемого примера: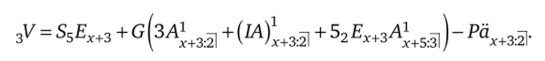

В общем виде:

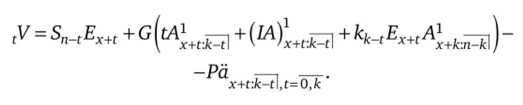
Мы рассмотрели формирование резерва на этапе, когда взносы уплачиваются страхователем. Теперь выведем формулу резерва на этапе, когда уплата взносов закончена. Снова построим схему данного этапа договора страхования (рис. 2.14).

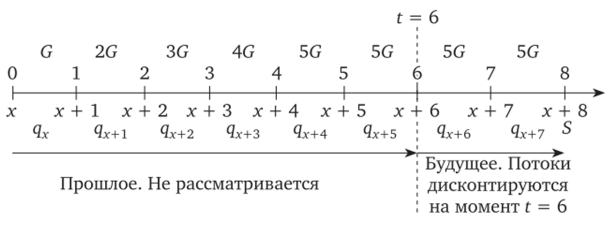
Рис. 2.14. Финансовые потоки страховых выплат для договора с рассроченными взносами. Срок уплаты взносов меньше срока страхования. Этап после уплаты взносов.

Рисунок 2.14 показывает, что из всех финансовых потоков на данном этапе остаются выплаты по смерти и дожитию, потока взносов нет. Следовательно, ОСС взносов равна 0. Ожидаемая выплата по дожитию формируется, как и прежде, S₂p_x+eV² = S₂E_x+6, а в общем виде S_n__tE_x+t.

Рассмотрим выплаты по смерти для нашего примера исходя из схемы:

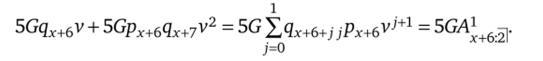
В общем виде:

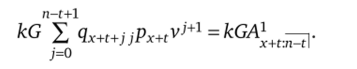
Таким образом, для рассматриваемого примера формула резерва: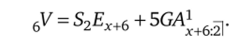

В общем виде:

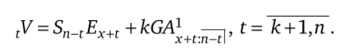
Все приемы, использованные в данном примере, могут применяться при выводе формул для расчета математического нетто-резерва и для других наборов условий по страховым выплатам и взносам.