Определение ошибки и численности выборки

Любое выборочное исследование, как бы старательно оно ни проводилось, содержит ошибку (погрешность). Эта погрешность вызвана исключительно тем обстоятельством, что исследуется не вся совокупность, а только ее небольшая часть. При этом погрешность связана с объемом выборочной совокупности (чем она больше, тем погрешность меньше), однако следует понимать, что одно из главных преимуществ выборочного наблюдения состоит в том, что изучению подвергается небольшая часть генеральной совокупности. Если выборка составляет 10%, а тем более 20% всей совокупности, возникает вопрос о ее целесообразности, практической возможности исследования и затратах на его проведение.

Важным вопросом при планировании выборочного исследования является исчисление и определение объема выборки. Многие неправильно считают, что величина выборки пропорционально зависит от объема генеральной совокупности. Такое мнение ошибочно. Объем выборки рассчитывается по достаточно простым формулам, и знание численности генеральной совокупности, например для повторного отбора, не является необходимым. Попутно заметим, что в статистике различаются большие выборки (п > 30), и малые выборки (п < 30). Впрочем, эта граница не является общепринятой.

Приведем три основных формулы выборочного наблюдения при повторном и бесповторном отборе (табл. 8.2).

Таблица 8.2

Основные формулы выборочного наблюдения

Показатель.	Повторный отбор	Бесповторный отбор
Средняя ошибка выборки, |д.
Предельная ошибка выборки, Л.
Численность выборки, (п, п')

В формулах а² — дисперсия (генеральная или выборочная), N — численность генеральной совокупности, пип' — численности повторной и бесповторной выборки, t — коэффициент доверия, связанный с вероятностью, Д — предельная ошибка выборки.

При определении доли (%) напомним, что а² = pq, где р — доля единиц, обладающих данным признаком, a q — доля единиц, не обладающих данным признаком.

Начнем с определения необходимой численности выборки. Как уже указывалось, объем (численность) случайной выборки определяем по простой формуле, и для ее исчисления необходимо знать три величины — t, а², А. Величина t — коэффициент доверия, связана с вероятностью, с которой мы намерены работать. По специальным таблицам (интеграл вероятности или функция Лапласа) фиксируем вероятность и находим t, например при вероятности 0,9 по таблице находим число 1,65. Это самая простая часть работы. Далее следует проставить в формулу величину дисперсии а² генеральной совокупности. Но ведь это сделать невозможно, ибо мы ее не знаем; можно было бы заменить ее выборочной дисперсией, но это тоже невозможно сделать, так как самой выборки еще нет. В некотором виде получается замкнутый круг. Какие есть способы найти хотя бы приближенные оценки дисперсии? Во-первых, можно использовать данные аналогичных нашему исследованию, во-вторых, можно обратиться к экспертам в данной области, в-третьих, можно «на глаз» отобрать 20—30 значений, по которым определяется требуемое значение в первом приближении (так называемое пилотажное исследование).

Приведенная выше методика определения численности выборки, ошибки выборки, а также фиксации желаемой нами вероятности при определении доверительных интервалов оценки ни в коем случае не должна создавать впечатления, что задача определения этих значений легка и однозначна. Как раз наоборот — все много сложнее. Поэтому представляется, что следовало бы дать сразу более детальное разъяснение возможных трудностей, способов их преодоления и нахождения оптимального решения.

Любое выборочное исследование, какие бы оно ни ставило перед собой конкретные и узкие задачи, неизбежно сталкивается с тем обстоятельством, что наиболее существенные признаки (а их несколько, 3—4, а иногда и более) выражены в разных единицах измерения, не говоря о том, что некоторые из них количественные, а другие качественные (пол, семейное положение, религиозная принадлежность и т. п.). Поэтому требуется рассчитывать отдельно необходимую для каждого признака численность выборки (наприте²

мер, по формуле и = ——-) ^и заранее оценивать размер дисперсии и допустимую погрешность, и часто бывает, когда для одного признака численность выборки, например, равняется 50, а для другого признака — 600. Очевидно, что при окончательном определении выборочной совокупности надо найти разумный компромисс и отдать предпочтение, конечно, наиболее существенным, главным признакам. Кроме того, весьма желательно определить для этих признаков допустимые доверительные интервалы и определить необходимую точность, которую возможно в некоторых случаях снизить или даже отказаться от данного признака.

Рассмотрим предельную ошибку выборки Д, которая определяет точность исследования и является разностью между неизвестным значением параметра и его оценкой, которую мы намерены получить в результате подсчета выборочных данных. Предельная ошибка состоит из двух частей р и t. Показатель р — эго средняя ошибка, a t — коэффициент доверия, заранее определяемый нами с таким расчетом, чтобы отклонение выборочной оценки от параметра было бы не очень большим. Предельная ошибка может выражаться в абсолютных величинах (рубли, граммы, метры), а может быть выражена в относительных величинах (например, допускается ошибка в 1, 5, 10%). Так, например, если параметр предположительно равен 500 денежным единицам, вполне возможно, что 10 денежных единиц это допустимая погрешность. Она может быть выражена как 2% или как 0,02, если 500 будет приравнено к 1.

Как раз здесь и кроется опасность неправильного определения этой ошибки для всех признаков. Если для одного признака вполне допустима ошибка в 5%, то для другого признака подобная ошибка повлечет за собой очень большое увеличение объема выборки. Покажем это на примере, где генеральная совокупность N= 7000. Рассмотрим два существенных признака', размер заработной платы и долю людей, удовлетворенных своей работой.

Известно скажем, что величина средней заработной платы оценивается в 25 тыс. руб. с, а = 4 тыс. руб. Принимая предельную ошибку в 5% и вероятность (надежность) 0,9, получаем, что объем выборки должен быть равен 28 (используется формула для определения численности повторной выборки, так как п и ri практически совпадают); а если бы мы зафиксировали вероятность 0,954, то объем выборки составил бы 41. Выборка невелика по объему, ибо совокупность однородна, что показывает коэффициент вариации 16%.

Рассмотрим второй признак. Известно (или получено при пробном исследовании), что только 12% людей были удовлетворены своей работой. При той же вероятности 0,954 и предельной ошибке в 5% численность выборки должна была составить 165 человек (при повторном отборе п = 169) — практически разница несущественна.

Необходимо отметить, что выбор точности в 5% скорее дань традиции и удобству, чем, возможно, реальной необходимости. Так при ошибке в 6% п = 117, а при ошибке в 4% численность выборки составляла бы 264. С учетом того, что увеличение выборки значительно удорожает исследование, к минимизации ошибки следует стремиться не всегда, а только тогда, когда это вызвано существом дела. В тех случаях, когда ошибка (для средней) выражена в процентах, в формуле для определения численности выборки вместо дисперсии должно быть проставлено значение коэффициента вариации (для согласования размерности).

Следует указать, что доверительная вероятность также оказывает большое влияние на величину выборки. Однако не стоит чрезмерно увеличивать надежность, это приводит к завышению объема выборки. Что касается величины дисперсии, то ее уменьшение возможно в двух случаях, а именно: когда сама генеральная совокупность сравнительно однородна, а также когда генеральная совокупность предварительно была разделена на районы, страты, серии и вместо общей дисперсии используется средняя из внутригрупповых.

Оценка неизвестной дисперсии для каждого признака зависит главным образом от квалификации статистика и сочетания его знаний, опыта и интуиции со знаниями специалиста-предметника, глубоко погруженного в данную тематику. Если же говорить об общих подходах, то, как уже упоминалось, оценка дисперсии для качественных признаков при не очень малых долях р vq дает как правило хорошие результаты. Так, при доле качественного признака 0,5; 0,4; 0,3 дисперсия составляет 0,25; 0,24; 0,21 соответственно, что не оказывает заметного влияния при определении ошибки и численности выборки. Что касается количественных признаков, то следует прежде всего ознакомиться с мнением заслуживающих доверия экспертов или с аналогичными исследованиями, проводившимся ранее или в других местах. Часто используется для определения дисперсии величина, а ~ R/6 (для симметричного распределения) или, а ~ R/5 (для распределения со значительной асимметрией).

Аналогично поступаем и с определением предельной ошибки выборки Л (в знаменателе), заранее определяя (чаще всего в процентах, в долях или в абсолютном выражении) допустимо приемлемую для каждого конкретного случая ошибку. В социальноэкономических исследованиях чаще всего допустимая ошибка находится в интервале от 1 до 10%, по умолчанию — 5%-ный уровень значимости. Определяя ошибку, естественно, исследователь стремится к ее снижению, минимизации. Однако следует помнить, что снижение ошибки ведет к значительному увеличению выборки, например, снижение ошибки на 1% может привести к увеличению выборки на 40%.

Проставив все полученные значения в формулу, получаем необходимый объем выборки. Необходимо особо отметить, что в формуле для определения численности выборки нет величины N— т. е. объема генеральной совокупности. Величина N появляется в формуле бесповторного отбора и способствует некоторому уменьшению численности выборки.

Рассчитав необходимый объем выборки, соизмеряем требуемый ее размер с нашими возможностями (чаще всего материального свойства): будут ли достаточны имеющиеся средства или нет? Если ответ будет отрицательным, то следует либо уменьшить коэффициент доверия, например с 1,65 до 1,44 (г.е. доверительную вероятность с 0,9 до 0,85), либо увеличить ошибку выборки, например с 5 до 7—8%. Поясним сказанное на примере.

Пример 8.1.

В вузе на дневном отделении обучаются 6820 студентов. Это генеральная совокупность. Ректорат интересуется многими аспектами жизни студентов, в частности их религиозностью (всех конфессий). Была проведена случайная бесповторная выборка п = 173 человек. При опросе 71 человек ответил, что они религиозны, а остальные заявили, что они не религиозны. Требуется определить с заданной вероятностью долю (%) религиозных студентов во всем вузе.

Решение

Прежде всего определяем долю религиозных студентов в выборке.

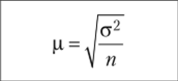
Доля неверующих студентов соответственно q = 1 — р. 1 — 0,41 = 0,59 или 102: 173 = 0,59. Фиксируем доверительную вероятность 0,92. По таблице интеграла вероятностей находим t = 1,76.

Далее выписываем формулу предельной ошибки бесповторной выборки для определения доли.

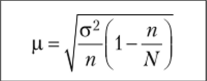
где pq — дисперсия альтернативного признака (0,41 • 0,59), и проставляем конкретные значения:

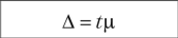
Поскольку выборочная доля р верующих составила 41%, а предельная ошибка 6,5%, то мы вправе сказать, что с вероятностью 0,92 доля верующих во всем вузе составляет 41 ±6,5%, или от 34,5 до 48,5%. Если ректорат не удовлетворен таким результатом (величина ошибки велика, а границы широки), то мы сможем предложить снизить ошибку до любого приемлемого уровня, но при условии, как правило, удорожания исследования, чаще всего за счет увеличения объема выборки. Например, при ошибке 3,25% необходимый объем выборки составит 692 (173 • 4), т. е. снижение ошибки в 2 раза влечет за собой увеличение выборки в 4 раза.

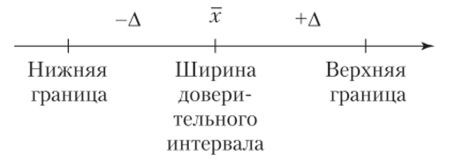
Подводя некий промежуточный итог сказанному выше, заключаем, что полученная предельная ошибка выборки (А = tx) используется для построения доверительного интервала, относительно которого можно утверждать с определенной, достаточно большой вероятностью, что он накрывает неизвестное значение параметра, т. е. значение неизвестной нам точно характеристики генеральной совокупности. Если, например, взять выборочное среднее значение, обозначенное х, и предельную ошибку А, то схематически эту ситуацию можно представить так:

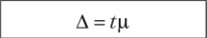
Этот результат является заключительным итогом определения возможной величины математического ожидания (т.е. неизвестного параметра). Утверждение, что он находится в таких границах, делается с определенной вероятностью. Попутно заметим, что границы интервала симметричны относительно средней оценки. Однако при оценке доли, если эта доля невелика, например меньше 0,1 (10%), расчет по формулам, указанным выше, дает недостаточно точные результаты. В действительности интервалы должны быть несимметричными, и они рассчитываются разными способами. На этом вопросе мы остановимся далее.

Следует также упомянуть, что отношение x/ji называется достоверностью средней величины, а величина к/х является точностью опыта — этот показатель выражает величину ошибки средней арифметической в процентах от самой средней арифметической. Точность опыта, не превышающая 5%, считается удовлетворительной.

Рассмотрим еще раз ситуацию, когда требуется установить доверительный интервал для доли (%). Например, производство некой продукции первого сорта на данном предприятии составляет 40%. Следовательно, 60% приходится на остальную продукцию.

В данном случае дисперсия определяется как pq = а². При выборке в 60 единиц средняя ошибка повторной выборки составляет.

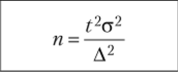
При условии, что N = 1000, средняя ошибка бесповторной выборки практически оказалась бы такой же; поправка (1 — n/N) дает снижение лишь на 0,0001.

Доверительные границы для доли при условии, что р и q не сильно отличаются друг от друга, как было показано выше, составляют 0,4 ± 0,0632 (0,3368 — 0,4632), т. е. отклонение от средней симметрично. Однако при величине доли меньше чем 0,1 и при сравнительно небольшой выборке (30—50), а таких случаев довольно много на практике (доля брака, доля двоек, доля людей альбиносов, процент (доля) студентов, свободно владеющих 3—4 иностранными языками и т. п.), следует использовать биномиальное распределение (или пуассоновское). В этом случае доверительные границы не являются симметричными. Определение нижней и верхней доверительной границы Р_н и Р_в определяется по асимптотической (приближенной) формуле.

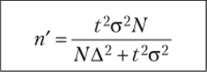
Эта формула несколько громоздка, но особенных трудностей при нахождении доверительных границ нет. Приведем пример.

Пример 8.2.

Выборочная совокупность составляет 40 единиц, а событие Л (например, брак или какое-либо другое редкое событие — р < 0,1) наблюдается три раза (k = 3). Необходимо с вероятностью 0,95 (t = 1,96) определить доверительные границы бракованных изделий во всей партии. По данным выборки доля бракованных изделий.

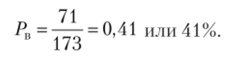
Подставляя конкретные значения, имеем.

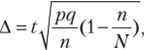
Р_п = 0,024 (2,4%); Р_в = 0,2 (20%), т.с. количество брака во всей партии (генеральной совокупности) будет находиться в пределах от 2,4 до 20%. Как очевидно, границы очень широки и не симметричны (2,4 < 7,5 < 20).

При тех же условиях, но для выборки п = 100 границы находились бы от 1 до 8% при значении k = 3 (3%).

В тех случаях, когда исследуется редкий признак, который не обнаружен в случайной выборке, но он (это известно заранее) присутствует в генеральной совокупности, и нет возможности провести повторное исследование или увеличить объем выборки, применяется несколько искусственный прием — определяется максимально возможное значение такого признака в генеральной совокупности по формуле.

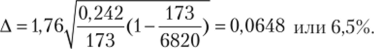
Например, при вероятности 0,95 t = 1,96, и при объеме выборки, например 100, имеем.

т.е. доля этого признака в генеральной совокупности может варьироваться от 0 до 3,7%.