Математическая модель метода electre III

Концепция псевдо-критериев основывается на том, что оценки альтернатив не обладают абсолютной точностью, что обеспечивает возможность различной трактовки разницы между оценками альтернатив. Для учета этого факта при определении отношения предпочтения S используются границы безразличия и предпочтения, которые позволяют учитывать степень превосходства одной альтернативы над другой по каждому… Читать ещё >
Математическая модель метода electre III (реферат, курсовая, диплом, контрольная)
Метод ELECTRE III является развитием метода ELECTRE II и предоставляет возможность более точного ранжирования альтернатив, которая достигается благодаря использованию псевдо-критериев, позволяющих учитывать неструктурированные данные.
Концепция псевдо-критериев основывается на том, что оценки альтернатив не обладают абсолютной точностью, что обеспечивает возможность различной трактовки разницы между оценками альтернатив. Для учета этого факта при определении отношения предпочтения S используются границы безразличия и предпочтения, которые позволяют учитывать степень превосходства одной альтернативы над другой по каждому критерию.
Для каждого критерия Kn вводится определяемая экспертно граница безразличия — qn, обозначающая несущественную с точки зрения ЛПР разницу между оценками двух альтернатив по этому критерию, которая позволяет сделать вывод о равнозначности сравниваемых альтернатив по данному критерию.
Для каждого критерия Kn вводится определяемая экспертно граница предпочтения — pn, обозначающая существенную с точки зрения ЛПР разницу между оценками двух альтернатив по этому критерию, которая позволяет сделать вывод о строгом превосходстве одной альтернативы над другой по данному критерию.
Поскольку граница предпочтения обозначает существенную с точки зрения ЛПР разницу между оценками альтернатив, а граница безразличия — несущественную разницу, граница предпочтения должна быть всегда больше границы безразличия:
pn > qn, n=1,N. (16).
Ранжирование альтернатив методом ELECTRE III основано на последовательном сравнении каждой пары альтернатив. В рамках этого сравнения для каждой пары альтернатив по каждому критерию Kn вычисляется индекс согласия SOn(Vi, Vk) по следующей формуле:
Для критериев с направлением максимизация:
1, если (Fin — Fkn)? pn
SOn(Vi, Vk) = (Fin — Fkn) / pn, если qn < (Fin — Fkn)< pn (17).
0, если (Fin — Fkn)? qn
Для критериев с направлением минимизация:
1, если (Fkn — Fin)? pn
SOn(Vi, Vk) = (Fkn — Fin) / pn, если qn <(Fkn — Fin)< pn (18).
0, если (Fkn — Fin)? qn
Таким образом,.
0? SOn(Vi, Vk)? 1. (19).
В (17) — (19) i=1,L, k=1,L, n=1,N.
Если SOn(Vi, Vk) = 1, то альтернатива Vi строго лучше альтернативы Vk по критерию Kn. Если, то присутствует нестрогое предпочтение альтернативы Vi альтернативе Vk по критерию Kn. Если SOn(Vi, Vk) = 0, то нет оснований полагать, что альтернатива Vi лучше альтернативы Vk по критерию Kn. Соответственно, чем выше значение индекса согласия SOn(Vi, Vk), тем альтернатива Vi лучше альтернативы Vk по критерию Kn.
После вычисления индексов согласия для каждой пары альтернатив по каждому критерию вычисляется индекс несогласия, отражающий, насколько одна альтернатива хуже другой по рассматриваемому критерию. При сравнении альтернатив Vi и Vk индекс несогласия по критерию Kn обозначается NEn(Vi, Vk) и вычисляется по следующей формуле:
Для критериев с направлением максимизация:
0, если (Fkn — Fin)? qn
NEn(Vi, Vk) = (Fkn — Fin) / vn, если qn < (Fkn — Fin) < vn (20).
1, если (Fkn — Fin)? vn
Для критериев с направлением минимизация:
0, если (Fin — Fkn)? qn
NEn(Vi, Vk) = (Fin — Fkn) / vn, если qn < (Fin — Fkn) < vn (21).
1, если (Fin — Fkn)? vn
Таким образом,.
0? NEn(Vi, Vk)? 1. (22).
В (20) — (22) i=1,L, k=1,L, n=1,N.
Если NEn(Vi, Vk) = 0, то нет оснований полагать, что альтернатива Vi хуже альтернативы Vk по критерию Kn. Если, то существуют основания полагать, что альтернатива Vi хуже альтернативы Vk по критерию Kn. Если NEn(Vi, Vk) = 1, то критерий Kn накладывает вето на утверждение, что альтернатива Vi лучше чем Vk. Соответственно, чем выше значение индекса несогласия NEn(Vi, Vk), тем альтернатива Vi хуже чем Vk по критерию Kn.
Для оценки превосходства одной альтернативы над другой по всем критериям вводится общий индекс согласия C (Vi, Vk), который рассчитывается как сумма произведений веса каждого критерия Pn, на индекс согласия по данному критерию SOn(Vi, Vk), где n — номер соответствующего критерия.
C (Vi, Vk) = (23).
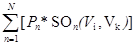
0? C (Vi, Vk)? 1 (24).
В (23) — (24) i=1,L, k=1,L.
Если C (Vi, Vk) = 1, то альтернатива Vi строго предпочитается альтернативе Vk по всем критериям, а если C (Vi, Vk) = 0, то нет оснований полагать, что альтернатива Vi лучше альтернативы Vk. Соответственно, чем выше значение общего индекса согласия C (Vi, Vk) тем альтернатива Vi предпочтительнее альтернативы Vk.
Для оценки того, насколько одна альтернатива хуже другой по всем критериям, вводится общее отношение нон-несогласия ND (Vi, Vk):
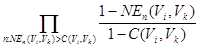
ND (Vi, Vk) = (25).
0? ND (Vi, Vk) < +? (26).
В (25) — (26) i=1,L, k=1,L.
Если ND (Vi, Vk) = 0, то как минимум один критерий накладывает вето на утверждение что альтернатива Vi лучше чем Vk. Если отношение нон-несогласия стремится к +?, то по всем критериям SOn(Vi, Vk) = 1 (т.е. по всем критериям альтернатива Vi строго лучше альтернативы Vk). Соответственно, чем меньше значение общего отношения нон-несогласия ND (Vi, Vk), тем альтернатива Vi хуже альтернативы Vk.
Для определения наличия отношения предпочтения между двумя альтернативами в методе ELECTRE III требуется одновременно учесть отношение согласия и отношение нон-несогласия, что осуществляется путем введения новой переменной — общего отношения предпочтения PR, вычисляемой путем перемножения общего индекса согласия и отношения нон-несогласия по соответствующей паре альтернатив:
PR (Vi, Vk) = ND (Vi, Vk)* C (Vi, Vk), i=1,L, k=1,L. (27).
0? PR (Vi, Vk) < +?, i=1,L, k=1,L. (28).
PR (Vi, Vk) = 0 в том случае, если как минимум 1 критерий накладывает вето на утверждение что альтернатива Vi предпочтительнее альтернативы Vk (ND (Vi, Vk) = 0) и/или нет оснований полагать, что альтернатива Vi лучше альтернативы Vk ни по одному из критериев (C (Vi, Vk) = 0).
Для определения отношения предпочтения между двумя альтернативами вводится задаваемая экспертно граница отношения предпочтения л, определяющая минимально достаточное с точки зрения ЛПР значение общего отношения предпочтения.
Согласно методу ELECTRE III, альтернатива Vi считается «не хуже чем» Vk, если значение PR (Vi, Vk) не меньше границы отношения предпочтения л. Граница отношения предпочтения определяется ЛПР и может быть как константой, так и функцией от некоторой переменной. Чем выше граница отношения предпочтения, тем выше «строгость» ранжирования альтернатив.
Процедура ранжирования альтернатив (присвоение альтернативам рангов) в методе ELECTRE III производится с использованием порядка, описанного в 2.1 для метода ELECTRE II.