Моделирование физических задач

КРАТКОЕ ИЗЛОЖЕНИЕ ПРОГРАММНОГО МАТЕРИАЛА С МЕТОДИЧЕСКИМИ УКАЗАНИЯМИ СТУДЕНТУ

На протяжении всей своей жизни человек ежедневно сталкивается с моделями и сам создает новые.

Важную роль при проведении исследований играют гипотезы (от греч. hypothesis — основание, предположение), т. е. определенные предсказания, предположительные суждения о причинно-следственных связях явлений, основанные на некотором количестве опытных данных, наблюдений, догадок. Формулирование и проверка правильности гипотез основываются, как правило, на аналогиях.

Под моделью (от лат. modulus — мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект-оригинал, сохраняя некоторые важные для данного исследования типичные его черты.

Процесс построения и использования модели называется моделированием (или замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием).

Модели в физике применяются во всех разделах:

в механике реальные тела заменены двумя моделями: материальная точка и твердое тело;

в термодинамике — идеальный газ;

в электричестве реально заряженные тела заменены моделями, называемыми «точечный заряд» и «распределенный заряд»;

в атомной физике существовало несколько моделей атомов: Томпсона, Резерфорда, планетарная модель, а также различные модели ядра — капельная и оболочечная.

Рассмотрим основные цели, преследуемые при моделировании в научной сфере.

• 1. Применение моделей при изучении и прогнозировании поведения сложных процессов и явлений.
• 2. Модели позволяют выявлять наиболее существенные факторы, формирующие те или иные свойства объекта, поскольку сама модель отражает лишь некоторые основные характеристики исходного объекта.
• 3. Если свойства объекта с течением времени меняются, то особое значение приобретает задача прогнозирования состояний такого объекта под действием различных факторов.

Итак, модель нужна для того, чтобы:

• 1) понять, как устроен конкретный объект: какова его структура, основные свойства, законы развития, саморазвития и взаимодействие с окружающей средой;
• 2) научиться управлять объектом или процессом, определять наилучшие способы управления при заданных целях и критериях;
• 3) прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект.

Модель — это инструмент, ориентированный в первую очередь на исследование поведения и свойств конкретного объекта в целях управления этим объектом или предсказания его свойств.

Теория — более абстрактное, чем модель, средство, основной целью которого является объяснение поведения или свойств не конкретного объекта, а некоторого класса объектов.

Теория содержит конечную или даже бесконечную совокупность конкретных моделей.

Ричард Фейнман:

«У нас всегда есть возможность опровергнуть теорию, но, обратите внимание, мы никогда не можем доказать, что она правильна. Предположим, что Вы выдвинули удачную гипотезу, рассчитали, к чему это ведет, и выяснили, что все ее следствия подтверждаются экспериментально. Значит ли это, что Ваша теория правильна? Нет, просто-напросто это значит, что Вам не удалось ее опровергнуть».

Моделирование физических задач Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений.

Задача о баскетболисте Разработать модель, позволяющую описать полет баскетбольного мяча, брошенного игроком в баскетбольную корзину.

Модель должна позволять:

вычислять положение мяча в любой момент времени;

определять точность попадания мяча в корзину после броска при различных начальных параметрах.

Исходные данные:

• — масса и радиус мяча ;
• — начальные координаты (x0, y0), начальная скорость и угол броска мяча a0;
• — координаты центра (x, y) и радиус R корзины.

Примем следующие гипотезы:

• — мяч будем считать материальной точкой массой, положение которой совпадает с центром масс мяча;
• — движение происходит в поле сил тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона;
• — движение мяча происходит в одной плоскости, перпендикулярной поверхности Земли и проходящей через точку броска и центр корзины;
• — пренебрегаем сопротивлением воздуха и возмущениями, вызванными собственным вращением мяча вокруг центра масс.

С учетом вышеизложенного, можно сформулировать постановку задачи о баскетболисте в следующем виде:

Определить закон движения материальной точки массой под действием силы тяжести, если известны начальные координаты точки и, ее начальная скорость и угол бросания. Центр корзины имеет координаты и. Вычислить точность броска, где определяется из условий:, , .

Таким образом, поиск решения задачи сводится к отысканию некоторых зависимостей искомых величин от исходных параметров модели.

Математическая постановка А) Векторная форма.

Найти зависимости от времени векторных параметров и из решения системы обыкновенных дифференциальных уравнений:

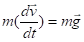
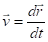
(2.1).

при следующих начальных условиях:

(2.2).

Вычислить параметр как.

(2.3).

где определить из следующих условий.

, .

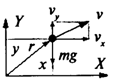
Б) Координатная форма Найти зависимости, и, из решения системы дифференциальных уравнений:

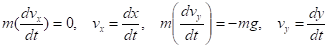
(2.5).

при следующих начальных условиях:

(2.6).

Вычислить параметр как.

(2.7).

где определить из следующих условий.

(2.8).

Из соотношений (2.5) получим.

(2.9).

Константы интегрирования найдем из начальных условий (2.6). Тогда решение задачи можно записать следующим образом.

(2.10).

Примем для простоты, что в момент броска мяч находится в начале координат и на одном уровне с корзиной т. е.

. (2.11).

Под дальностью броска будем понимать расстояние, которое пролетит мяч от точки броска до пересечения с горизонтальной плоскостью, проходящей через кольцо корзины.

Из соотношений (2.10) для координат, с учетом условий (2.11), дальность броска выразится следующим образом:

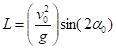
(2.12).

Тогда точность броска с учетом (2.7) будет равна.

(2.13).

Например, при броске мяча со штрафной линии можно принять следующие исходные данные:

Тогда из (2.12) и (2.13) имеем L = 4,225 м; = 0 м.

Реализация модели на компьютере.

1) Название задачи описать полет баскетбольного мяча, брошенного игроком в баскетбольную корзину.

Название программы Basketball.

Язык программирования Fortran.

Компьютер IBM PC Pentium.

2) Описание Приводится математическая постановка задачи и описание метода ее решения.

3) Входные данные Входными данными являются радиус и масса мяча, его начальные координаты и скорость, угол бросания, координаты корзины.

4) Выходные данные.

Траектория центра мяча, расчетная величина дальности и точность броска.

5) Ошибки.

При вводе исходных данных предусмотреть контроль:

все вводимые значения должны быть положительны;

угол бросания лежит в пределах от 5 до 85 градусов;

начальная скорость мяча лежит в пределах от 0 до 30 м/с;

горизонтальная координата центра корзины больше начальной горизонтальной координаты мяча.

6) Тестовые примеры.

При получаем:

Под адекватностью модели будет пониматься степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи.

Задача № 2. Оформить самостоятельно аналогично задаче 1.

Модель движения лодки Лодку оттолкнули от берега и, разогнав, отпустили при некоторой начальной скорости. Необходимо исследовать движение лодки. Полученные результаты представить в графическом виде.

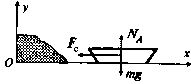
Рассматривается движение лодки в воде с начальной горизонтальной скоростью под действием силы тяжести, архимедовой выталкивающей силы и силы сопротивления движению, приложенных к центру масс. Так как лодка держится на плаву (движение по вертикали отсутствует), то архимедова выталкивающая сила уравновешивает силу тяжести .

Разработку модели будем выполнять при следующих предположениях:

• 1. Объектом исследования является лодка, совершающая поступательное движение в горизонтальной плоскости.
• 2. Лодку принимаем за материальную точку массы, положение которой совпадает с центром масс.
• 3. Движение лодки под действием приложенной системы сил подчиняется основному уравнению динамики (второму закону Ньютона).
• 4. Величина силы сопротивления воды прямо пропорциональна скорости лодки и противоположна по направлению:, где — коэффициент пропорциональности (величина постоянная).

Требуется определить скорость лодки как функцию времени и графически отобразить эту зависимость.

Задача № 3 Движение точки под действием центральных сил.

Требуется исследовать параметры движения космического корабля вблизи планеты. Масса, начальное положение и начальная скорость корабля известны.

Постановка задачи для моделирования Космический корабль массой движется из положения с координатами с начальной скоростью под действием силы притяжения, направленной к неподвижному центру. Требуется определить координаты и компоненты вектора скорости космического корабля как функции времени, а также траекторию его движения.

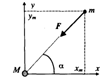
Построение модели выполняем при следующих допущениях:

объектом исследования является космический корабль, принимаемый за материальную точку;

параметрами модели являются координаты и скорость корабля;

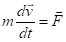
движение корабля происходит в одной плоскости и подчиняется основному уравнению динамики (второму закону Ньютона): ;

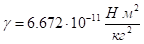
величина (модуль) силы притяжения к центру определяется законом всемирного тяготения, где — гравитационная постоянная, — расстояние между точкой массой и центром притяжения, имеющим массу .

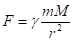
Математическая постановка Найти решение задачи Коши для следующей системы уравнений.

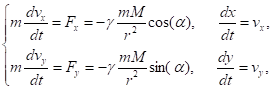
(1).

при начальных условиях.

.

Решение задачи.

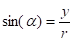
Принимая во внимание, что, и сокращая в (1) массу корабля, получаем.

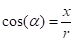
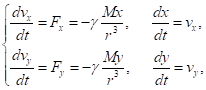
Решение задачи будем искать с использованием метода конечных разностей.

Метод конечных разностей — широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на разностные коэффициенты, что позволяет свести решение дифференциального уравнения к решению его разностного аналога, т. е. построить его конечно-разностную схему.

Так, заменив производную в обыкновенном дифференциальном уравнении на конечную разность.

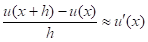
получаем аппроксимированную форму (конечно-разностную схему) Последнее выражение носит название конечно-разностного уравнения, а его решение соответствует приближённому решению первоначального дифференциального уравнения.

Заменим производные их разностными аналогами:

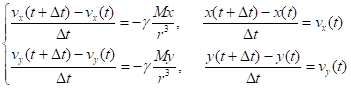
(2).

Из полученной системы разностных уравнений можно выразить скорости и перемещения:

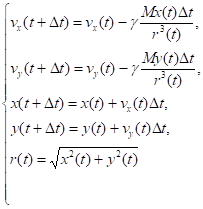
(3).

Анализ результатов На рис. 2 показаны траектории движения космического аппарата, полученные решением системы уравнений (3) при различных начальных скоростях.

При проведении расчетов принято: (масса Земли), космический корабль находится в начальной точке с координатами.

Начальная скорость направлена по горизонтали вправо. Шаг интегрирования выбран равным 0,01 с.

Поскольку радиус Земли R равен, ускорение свободного падения оценивается величиной 9,81 м/с2 (приближенные значения); для орбиты, находящейся над поверхностью планеты на высоте, первая и вторая космические скорости соответственно равны:

.

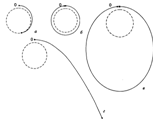
Рис 2. Траектории движения космического корабля при разных начальных скоростях: (a), (б), (в) и (г); во всех вариантах; пунктиром обозначена поверхность планеты.

Задача № 4.

Исследовать движение планеты в системе двух звезд. Массы планеты, звезд, их начальное положение и скорости известны.

Концептуальная постановка Планета массой движется из положения с координатами с начальной скоростью под действием сил притяжения и звезд неподвижной двойной системы. Положения и массы звезд определяются величинами, и соответственно. Требуется определить координаты и скорость планеты как функции времени, а также траекторию ее движения.

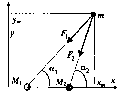
Построение модели выполняем при следующих допущениях:

объектом исследования является планета, принимаемая за материальную точку;

параметрами модели являются координаты и скорость планеты;

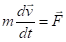
движение планеты происходит в одной плоскости и подчиняется основному уравнению динамики (второму закону Ньютона): ;

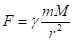
величина (модуль) силы притяжения к центру звезды определяется законом всемирного тяготения, где — гравитационная постоянная, r — расстояние между центром планеты и центром звезды.

Математическая постановка Найти решение задачи Коши для следующей системы уравнений:

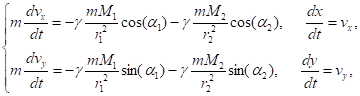
(1).

где.

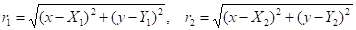
При начальных условиях.

(2).

Решение Для решения задачи используем численный метод. Заменяем производные разностным аналогом и получаем следующую систему разностных уравнений:

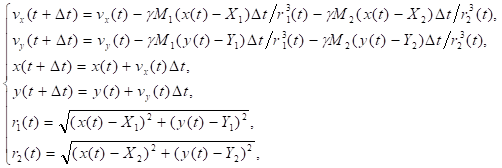
(3).

Анализ результатов Траектории движения планеты в системе двух неподвижных звезд при различных исходных данных приведены на рис. 4. Значения исходных данных выбраны произвольно и не соответствуют параметрам реальных систем. При проведении расчетов по формулам (3) принято, что первый центр притяжения, находится в начале системы координат, второй центр притяжения расположен в точке, планета находится в начальной точке с координатами и имеет начальную скорость, направленную по горизонтали вправо. Шаг интегрирования по времени во всех вариантах принят равным .

Рассмотрены следующие варианты движения планеты:

М1 = 2 * 1023 кг, М2 = 2 * 1023 кг, vx0 = 1,2 * 103 м/с (рис. 4а);

М1 = 5 * 1022 кг, М2 = 2,5 * 1023 кг, vx0 = 1,25 * 103 м/с (рис. 4б);

М1 = 2 * 1024 кг, М2 = 2 * 1024 кг, vx0 = 6 * 103 м/с (рис. 4в);

М1 = 2 * 1024 кг, М2 = 2 * 1024 кг, vx0 = 5 * 103 м/с (рис. 4г).

Приведенные результаты показывают, что движение планеты под действием двух центральных сил оказывается в значительной степени неустойчивым. Сравнительно небольшие изменения исходных данных приводят к качественному изменению характера движения планеты (сравните рис. 4а и 4б, 4 В и 4г).

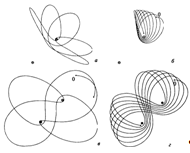
Рис. 4. Некоторые траектории движения планеты в поле действия двух центральных сил.

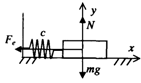
Задача № 5. Гармонический осциллятор Тело, лежащее на гладкой горизонтальной плоскости, прикреплено к неподвижной стене пружиной. Исследовать колебательные движения тела. Масса тела и жесткость пружины известны.

Примем следующие предположения:

• 1) объектом исследования является поступательно движущееся тело массой, принимаемое за материальную точку;
• 2) движение тела подчиняется второму закону Ньютона;
• 3) тело находится под действием трех сил: силы тяжести, реакции поверхности и силы упругости пружины. Так как поверхность гладкая, то силой трения пренебрегаем;
• 4) тело совершает прямолинейные колебательные движения, так как сила тяжести уравновешивается силой реакцией поверхности ;
• 5) в уравновешенном состоянии центр масс тела находится в положении с координатами ;
• 6) при малом растяжении пружины величину возникающей в ней силы упругости можно представить линейной зависимостью (закон Гука), где — растяжение пружины (отклонение тела от положения равновесия), — жесткость пружины. Направлена сила в сторону положения равновесия;
• 7) принимая, что в некоторый момент пружину растянули на величину и сообщили телу скорость, требуется определить координату и скорость тела как функции времени.

Математическая постановка С математической точки зрения имеем задачу Коши с начальными условиями:

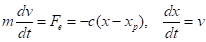
(19).

(20).

Требуется найти решение данной задачи.

Решение.

Введем обозначение для производных по времени:

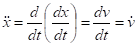
Тогда, принимая, обыкновенное дифференциальное уравнение (19) можно переписать в виде:

(21).

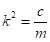
где — квадрат частоты свободных колебаний тела около положения равновесия. Период свободных колебаний выражается через циклическую частоту .

Уравнение (21) называется дифференциальным уравнением свободных колебаний материальной точки. Точка совершает гармонические колебания. Решение данного однородного линейного уравнения с постоянными коэффициентами можно представить в виде:

где — амплитуда свободных колебаний, — начальная фаза колебаний, определяемые из начальных условий.

Из этих выражений найдем и :

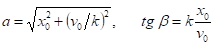
Решение рассматриваемой задачи можно получить численно, заменяя производные их приближенными разностными аналогами и переходя к системе разностных уравнений:

Анализ результатов.

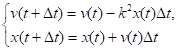
Принимая при выполнении расчетов.

получаем:

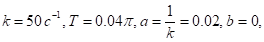
На рис. 8 приведены численные результаты определения положения материальной точки при разных шагах интегрирования. Видно, что с уменьшением величины значения, полученные при численных расчетах, стремятся к точному решению.

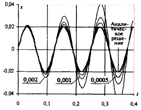
Рис. 8. Влияние величины шага по времени на точность решения.

Изложенный численный способ решения задач позволяет включить в уравнение движения нелинейную зависимость силы упругости пружины от величины растяжения. На рис. 9 представлены результаты численного решения рассмотренной задачи для нелинейных зависимостей силы от растяжения, приводящих к следующим системам разностных уравнений:

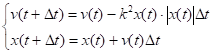
(знак модуля использован для учета направления действия силы в зависимости от положения тела) при и.

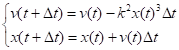
при. Жесткость пружины принималась равной .

Результаты, приведенные на рис. 9, свидетельствуют о незатухающих гармонических колебаниях тела во всех рассмотренных случаях. При этом с увеличением показателя степени при величине растяжения пружины происходит увеличение амплитуды и уменьшение частоты колебаний.

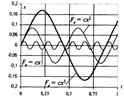
Рис. 9 Влияние вида зависимости силы от растяжения пружины на колебания тела.

Определенный интерес представляет анализ зависимости между положением тела и его скоростью, называемой фазовой траекторией. Для этого используют графическое представление процесса в системе координат «положение точки — скорость точки». Для этого представим точное решение в виде:

Исключение времени с помощью тригонометрических формул (сложение полученных соотношений) приводит к уравнению эллипса в системе координат .

На рис. 10 показаны найденные численно фазовые траектории для трех рассмотренных выше задач, имеющих разные зависимости сил упругости от удлинения пружин.

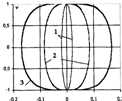
Рис. 10. Фазовые траектории точки при различных законах упругости

(1:; 2: 3:).

Усложним задачу введением дополнительной силы сопротивления движению. Такая ситуация возможна, если тело погружено в жидкость (рис. 11а) или если в рассматриваемую схему добавлен масляный демпфер, гасящий колебания (рис.11б). В последнем случае вязкое масло при перетекании внутри цилиндра создает дополнительное сопротивление движению.

Наличие сил вязкого трения приводит к необходимости добавления новой гипотезы при постановке задачи. Подобную гипотезу можно сформулировать следующим образом.

Сила вязкого трения прямо пропорциональна скорости тела и направлена против направления его движения: (- коэффициент сопротивления, величина постоянная).

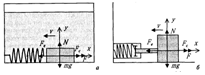
Рис. 11. Схемы конструкций с вязкими средами: жидкостью (а); масляным демпфером (б).

С учетом данной гипотезы, соотношения (19) в математической постановке следует заменить уравнениями следующего вида:

.

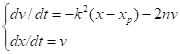
где ,.

Систему разностных уравнений в этом случае можно представить следующим образом:

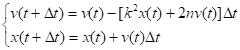
На рис. 12 показаны изменения координаты и скорости тела, полученные для условий (большое значение коэффициента сопротивления выбрано для наглядности результатов), шаг интегрирования t = 10−5 с.

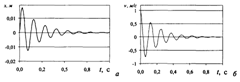
Рис. 12. Координата (а) и скорость (б) центра масс тела в вязкой среде.

На рис. 13 представлена фазовая траектория для тела, совершающего колебания в вязкой среде. В отличие от предыдущей задачи, наличие сопротивления (диссипации механической энергии) приводит к тому, что фазовая траектория оказывается спиралью с уменьшающимся радиусом, стремящимся к нулю. Это соответствует полной остановке механической системы.

Рис. 13. Фазовая траектория движения точки в вязкой среде.

Вынуждающие колебания Рассмотрим ситуацию, когда к телу (рис.11) приложена горизонтальная гармоническая сила, величина которой изменяется по закону с амплитудой и циклической частотой. Система уравнений преобразуется в этом случае к виду:

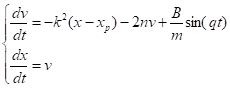
Система разностных уравнений может быть представлена следующим образом:

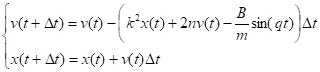
На рис. 14 представлена координата тела при вынужденных колебаниях как функция времени. При выполнении вычислений принято: (без учета вязкости), .

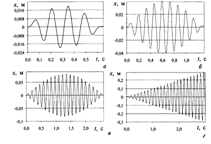
Рис. 14. Координата тела как функции времени при вынужденных колебаниях с частотами (a), (б), (в) и .

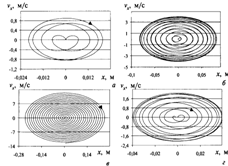
Рис. 15. Фазовые траектории при вынужденных колебаниях тела с частотой (a), (б), (в) и (г).

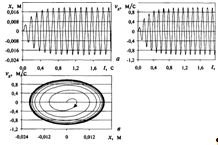
Рис. 16. Координата (а) и скорость (б) как функция времени, фазовая траектория (в) движения тела при вынужденных колебаниях в вязкой среде.

Задача № 6 об остывании кофе Природа переноса тепла от кофе к окружающему пространству сложна и в общем случае включает в себя механизмы конвекции, излучения, испарения и теплопроводности. В том случае, когда разность температур между объектом и окружающей средой не очень велика, скорость изменения температуры объекта можно считать пропорциональной этой разности температур.

Это утверждение более строго можно сформулировать на языке дифференциального уравнения:

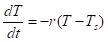
— закон теплопроводности Ньютона где — температура тела, — температура окружающей среды, r — «коэффициент остывания».

«Коэффициент остывания» зависит от механизма передачи, площади тела, находящегося в контакте со средой и тепловых свойств самого тела.

Множество процессов, происходящих в природе, описываются дифференциальными уравнениями, важно уметь решать эти уравнения.

Рассмотрим уравнение первого порядка вида.

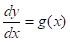
В общем виде аналитического решения уравнения не существует.

Алгоритм Эйлера Типичный метод численного решения дифференциальных уравнений включает в себя преобразование дифференциального уравнения в конечно-разностное.

Проанализируем уравнение Положим, что при функция принимает значение. Поскольку уравнение описывает изменение функции в точке, то можно найти приближенное значение функции в близлежащей точке, если приращение аргумента мало.

В первом приближении предполагается, что функция или скорость изменения, постоянна на отрезке от до .

В этом случае приближенное значение функции в точке определяется выражением Повторим процедуру еще раз и найдем значение y в точке.

Это правило можно обобщить и вычислить приближенное значение функции в любой точке по итерационной формуле — метод касательных (метод Эйлера).

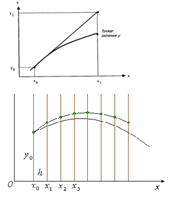
В методе Эйлера предполагается, что скорость изменения функции на отрезке от до постоянна, а наклон касательной вычисляется в начальной точке отрезка.

Графическая интерпретация метода Эйлера.

Пример:

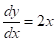
c начальным условием в точке. Находим приближенное значение функции в точке .

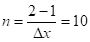
Выбираем, тогда число шагов равно .

Если после проведенных вычислений окажется, что выбранная величина приращения слишком велика, нам придется повторить вычисления с меньшим значением .

ПАДЕНИЕ ТЕЛ.

Опыты Галилея с падающими телами Галилей впервые выяснил, что тяжелые предметы падают вниз так же быстро, как и легкие. Чтобы проверить это предположение Галилео Галилей сбрасывал с Пизанской башни в один и тот же момент пушечное ядро массой 80 кг и значительно более легкую мушкетную пулю массой 200 г. Оба тела имели примерно одинаковую обтекаемую форму и достигли земли одновременно. До него господствовала точка зрения Аристотеля, который утверждал, что легкие тела падают с высоты медленнее тяжелых.

Рассмотрим одномерное движение, для описания которого нужна только одна пространственная координата.

Известно, что мгновенные координаты, скорость и ускорение материальной точки можно определить как:

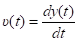
(1).

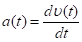
(2).

Второй закон движения Ньютона:

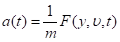
(3).

где — равнодействующая сила, — инертная масса.

В общем случае сила зависит от координаты, скорости и времени.

Для описания движения материальной точки необходимо решить систему двух дифференциальных уравнений первого порядка (1) и (2).

Уравнения (1) и (2) объединяют в одно дифференциальное уравнение второго порядка относительно координаты:

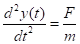
В отсутствие сопротивления воздуха все тела независимо от их массы, размеров и состава на одинаковом расстоянии от земной поверхности имеют одинаковое ускорение. Такое идеализированное движение, при котором сопротивлением воздуха пренебрегают, называется «свободным падением».

g = 9.8 м/с2 .

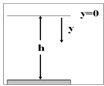
(4).

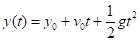
(5).

В соответствии с законом тяготения, сила Ньютона, действующая на тело массой равна:

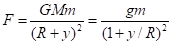
(6),.

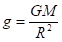
где — расстояние от поверхности Земли, — радиус Земли, — постоянная всемирного тяготения, — масса Земли, .

Другой важной модификацией задачи о свободном падении является учет тормозящей силы, обусловленной сопротивлением воздуха. Направление этой тормозящей силы должно быть противоположно скорости движения тела.

Рассмотрим сначала падение материальной точки. Тормозящая сила направлена вверх, как показано на рисунке. Полную силу, действующую на материальную точку, можно записать в виде.

(7).

В общем случае зависимость от скорости необходимо определять эмпирически, проводя конечную серию наблюдений положения тела.

• 1 способ: измерение координаты как функции и получении зависимости скорости и ускорения от времени.
• 2 способ: для функции предполагается определенный вид зависимости от скорости, и эта формула используется для нахождения функции. Если значения функции согласуются с экспериментальными, то предложенная зависимость считается экспериментально подтвержденной.

Наиболее общими зависимостями силы сопротивления от скорости являются.

(8а).

(8б).

и зависят от свойств среды и геометрии тела.

Ввиду того, что функция возрастающая, существует предельная, или установившаяся скорость, соответствующая условию и нулевому ускорению. Эту скорость можно найти из (7) и (8).

В результате получим:

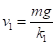
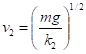
(9).

соответственно для линейного и квадратичного случаев.

Используя (8) и (9), выпишем для линейного и квадратичного случаев:

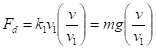
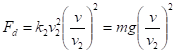
Отсюда равнодействующую силу, действующую на падающее тело, можно записать в виде.

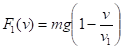
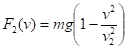
Поскольку аналитически решить уравнения движения (10).

(10).

с равнодействующей силой, определяемой выражением.

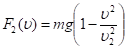
не просто, мы вынуждены прибегнуть к численным методам.

Метод Эйлера просто обобщается на случай решения дифференциального уравнения второго порядка.

• 1. переписываем уравнение (10) в виде системы двух дифференциальных уравнений первого порядка.
• 2. Обозначим через? t шаг по времени, тогда момент времени tn, соответствующий n-му шагу, равен

(11).

3. Обозначим также через, и значения ускорения, скорости и координаты на n-ном шаге,.

.

Прямое обобщение метода Эйлера принимает вид.

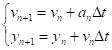
(12).

где — скорость в конечной точке интервала вычисляется через — производную скорости в начальной точке этого интервала.

Аналогично — координата в конечной точке интервала вычисляется через — производную координаты в начальной точке интервала.

Использованный алгоритм численного решения дифференциального уравнения не является единственным.

Например, одно простое изменение выражений (12) состоит в том, чтобы определять через — скорость в конечной точке интервала, а не в начальной точке. Запишем такой модифицированный метод Эйлера в следующем виде:

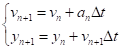
(13).

Численное интегрирование уравнений Ньютона Существует несколько конечно-разностных методов решения уравнений движения Ньютона с непрерывными силами.

!!! Важно помнить о том, что успешное использование численного метода определяется не только тем, насколько хорошо он приближает производную на каждом шаге, но и тем, насколько хорошо он аппроксимирует интегралы движения, например полную энергию.

Множество алгоритмов, используемых в настоящее время, свидетельствует о том, что ни один метод не превосходит по всем параметрам все остальные.

Рассмотрим одномерное движение частицы и запишем уравнения Ньютона в виде.

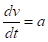
(1).

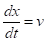
(2).

Целью всех конечно-разностных методов является вычисление значений и (точка в «фазовом пространстве») в момент времени .

!!! Величину шага надо выбирать таким образом, чтобы метод интегрирования порождал устойчивое решение.

Один из способов проверки устойчивости метода заключается в контроле величины полной энергии и обеспечении того, чтобы она не отклонялась от начального значения в случае, когда полная энергия сохраняется.

Достаточно большое значение шага приводит к не сохранению полной энергии и неустойчивым решениям для и, т. е. к таким численным решениям, которые все больше отклоняются с течением времени от истинного решения.

Суть многих алгоритмов можно понять, разлагая.

и в ряд Тейлора.

Запишем.

(3).

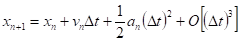
и (4).

Хорошо известный метод Эйлера эквивалентен сохранению в (3)-(4) членов :

(5) и.

(6).

Поскольку мы удержали в формулах (5)-(6) члены порядка, то «локальная» погрешность (погрешность на шаге) составляет величину. Однако от шага к шагу погрешности накапливаются, поэтому можно предполагать, что «глобальная» погрешность, представляющая собой суммарную погрешность за рассматриваемый промежуток времени, будет величиной .

Эта оценка погрешности вполне правдоподобна, поскольку число шагов, на которое разбивается временной интервал, пропорционально .

Следовательно, порядок глобальной погрешности увеличивается в раз по отношению к локальной погрешности. Метод Эйлера является асимметричным, поскольку он продвигает решение на один временной шаг, а использует при этом информацию о производной только в начальной точке интервала!

Для полноты изложения повторим алгоритм Эйлера-Кромера или приближение по «последней точке»:

(7).

(8).

Пожалуй, самый очевидный путь улучшения метода Эйлера состоит в использовании для вычисления нового значения координаты средней на отрезке скорости.

Соответствующий метод средней точки можно записать в виде.

(9).

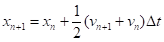
(10).

Заметим, что если подставить выражение (9) для в (10), то получим.

.

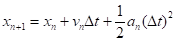
Следовательно, метод средней точки — метод второго порядка точности по координате и первого порядка точности по скорости. Хотя приближение по средней точке дает точные результаты для случая постоянного ускорения, в общем случае оно не приводит к значительно лучшим результатам, чем метод Эйлера.

На самом деле оба метода одинаково плохие, поскольку с каждым шагом погрешности увеличиваются.

Метод полушага относится к методам более высокого порядка точности с ограниченной погрешностью. Принимается, что средняя скорость на отрезке равна значению скорости в середине отрезка.

Метод полушага можно записать в виде.

(12а).

(12б) Заметим, что метод полушага не является «самостартующим», т. е. формулы (12) не позволяют вычислить. Это неудобство можно преодолеть, положив.

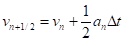
(12в) Метод полушага получил широкое распространение в учебной литературе.

Один из наиболее известных алгоритмов высокого порядка приписывается Верле.

По аналогии с (3−4) запишем разложение в ряд Тейлора для :

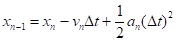
Если сложить (3)-(4) и (12) соответственно, то получим.

(14).

Или (15).

Аналогично вычитание разложений в ряд Тейлора для и дает.

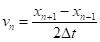
(15б) При этом связанная с алгоритмом Верле (15) глобальная погрешность имеет третий порядок для координаты и второй порядок для скорости.

Однако скорость не участвует в интегрировании уравнений движения.

В литературе по численному анализу алгоритм Верле называется «неявной симметричной разностной схемой».

Другой полезный алгоритм, в котором нет накопления погрешности округления, присущей алгоритму Верле, Бимана и Шофилда.

Запишем алгоритм Бимана в следующем виде:

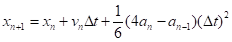
(21а).

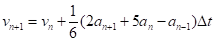
(21б) Заметим, что точность расчета траекторий по схеме (21) не выше, чем в алгоритме Верле. Ее преимущество заключается, пожалуй, в том, что обычно она лучше сохраняет энергию.

Методы Рунге — Кутта второго порядка Пусть дано дифференциальное уравнение первого порядка:

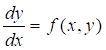
с начальным условием, .

В окрестности точки x0 функцию разложим в ряд Тейлора:

.

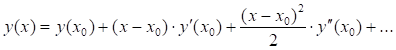
который можно применить для приближенного определения искомой функции. Для уменьшения погрешности метода интегрирования дифференциального уравнения необходимо учитывать большее количество членов ряда. Однако при этом возникает необходимость аппроксимации производных от правых частей дифференциального уравнения. Основная идея методов Рунге-Кутта заключается в том, что производные аппроксимируются через значения функции в точках на интервале [x0, x0+h], которые выбираются из условия наибольшей близости алгоритма к ряду Тейлора. В зависимости от старшей степени, с которой учитываются члены ряда, построены вычислительные схемы Рунге-Кутта разных порядков точности.

Так, например, общая форма записи метода Рунге — Кутта второго порядка следующая:

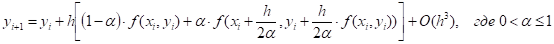
(8.19).

Решение ОДУ, полученное по этой схеме имеет погрешность .

Для параметра наиболее часто используют значения.

и.

Рассмотрим первый вариант метода Рунге — Кутта второго порядка.

При формула (8.19) примет вид:

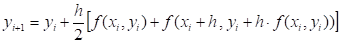
(8.20).

Формулу (8.20) можно представить в виде следующей схемы:

.

.

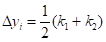
где ,.

Это метод Рунге — Кутта второго порядка (1-ый вариант).

В случае второго варианта метода Рунге — Кутта второго порядка принимают Тогда формула (8.19) примет вид:

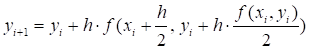
(8.21).

Представим формулу (8.21) в виде схемы:

.

.

где ,.

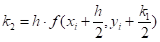
Это метод Рунге — Кутта второго порядка (2-ой вариант).

Метод Рунге — Кутта четвертого порядка Методы Рунге — Кутта третьего и четвертого порядков можно вывести аналогично тому, как это делалось при выводе методов первого и второго порядков.

Не будем воспроизводить эти выкладки, а приведем формулы, описывающие метод четвертого порядка, один из самых применимых методов интегрирования ОДУ. Этот метод применяется настолько широко, что в литературе просто называется «методом Рунге — Кутта» без указаний на тип и порядок. Этот классический метод Рунге — Кутта описывается системой следующих соотношений, приведенных на блок-схеме:

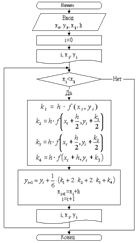
Рис. 8.8 Блок-схема метода Рунге-Кутта

Пример для тренировки.

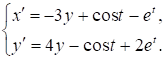
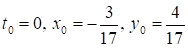
Решить систему при данных начальных условиях методом Рунге-Кутта.

t1=10, N=1000.

z1=-3*y+cos (t)-exp (t).

z1=F1(t, x, y).

z2=4*y-cos (t)+2*exp (t).

z2=F2(t, x, y).

dt=(t1-t0)/N.

do i=0:N.

t (i+1)=t (i)+dt*i.

kx1=dt*F1(t (i), x (i), y (i)).

ky1=dt*F2(t (i), x (i), y (i)).

kx2=dt*F1(t (i)+dt/2,x (i)+kx½, y (i)+ky½).

ky2=dt*F2(t (i)+dt/2,x (i)+kx½, y (i)+ky½).

kx3=dt*F1(t (i)+dt/2,x (i)+kx2/2,y (i)+ky2/2).

ky3=dt*F2(t (i)+dt/2,x (i)+kx2/2,y (i)+ky2/2).

kx4=dt*F1(t (i)+dt, x (i)+kx3,y (i)+ky3).

ky4=dt*F2(t (i)+dt, x (i)+kx3,y (i)+ky3).

x (i+1)=x (i)+1/6*(kx1+2*kx2+2*kx3+kx4).

y (i+1)=y (i)+1/6*(ky1+2*ky2+2*ky3+ky4).

end do.

ПРИМЕНЕНИЕ МЕТОДА РУНГЕ-КУТТА К ЗАДАЧЕ О ПАДЕНИИ ТЕЛ.

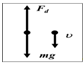
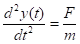
Задача: вычислить, в момент времени .

Решение:

Перепишем полученное дифференциальное уравнение второго порядка.

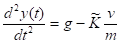
в виде системы дифференциальных уравнений первого порядка.

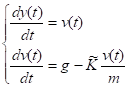
н.у.: ,.

Алгоритм:

Обозначим.

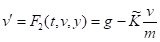
запишем начальные условия.

.

Определим шаг по времени .

Запишем коэффициенты метода Рунге_Кутта:

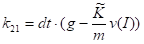
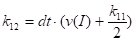
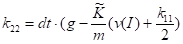
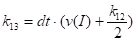
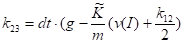
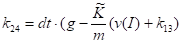
Выразим искомые значения скорости и координаты через коэффициенты:

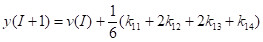
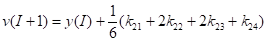
Изобразим на графике, .

Движение тел в поле тяжести Земли.

Предположим, что на снаряд действует только сила тяжести, равная. Если пушка расположена в точке с координатами (0, 0, 0), то снаряд будет двигаться по траектории, которая описывается следующими уравнениями:

где — скорость снаряда вдоль ствола пушки, — угол между стволом пушки и горизонтом (ось X), — время, — ускорение свободного падения в поле тяжести Земли.

Подставляя из первого уравнения во второе, находим уравнение траектории движения снаряда:

Из этого уравнения находим максимальную дальность стрельбы (при этом) и максимальную высоту полёта (первая производная по координате равна нулю):

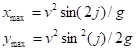
Из первого уравнения видно, что максимальная дальность полёта снаряда достигается при стрельбе под углом .

Учтем силу сопротивления движению Рассмотрим ядро массой с начальной скоростью, направленной под углом к горизонту (рис а). На него действуют сила тяжести и тормозящая сила, равные соответственно и, а направление последней противоположно скорости (рис. б).

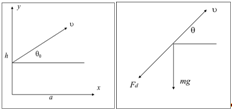
Запишем уравнение движения Ньютона для компонент и :

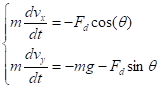
(15).

Определим максимальное расстояние от точки бросания, на которое улетит пушечное ядро радиусом 4 см.

Предположим, что для тела такого размера и характерной скорости .

Поскольку, а, уравнения (15) можно переписать в виде.

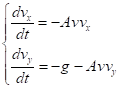
(16).

где. Заметим, что уравнения (16), описывающие изменения и, содержат модуль скорости: .

Следовательно, в случае силы квадратичной зависимости силы сопротивления от скорости, невозможно найти вертикальную составляющую движения падающего тела, не зная горизонтальную.

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ Пример

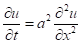
Используя метод сеток, решить уравнение теплопроводности (уравнение параболического типа): при заданных начальных условиях: и граничных условиях:, , где. Решение найти при, для c четырьмя десятичными знаками, считая .

Решение.

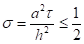
Будем пользоваться явной конечно-разностной схемой, т. е. решение на верхнем временном слое получается сразу по значениям сеточных функций на нижнем временном слое, где решение известно. Она является условно устойчивой. Условие, накладываемое на сеточные характеристики и, состоит в том, что .

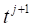
Алгоритм перехода на новый временной слой с использованием явной схемы можно представить в виде.

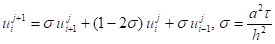
nx=6.

sig=1/6.

delx=0.6 разность конечного и начального значений.

h=delx/nx число узлов координатной сетки.

tau=h²*sig шаг по времени, определенный из условия устойчивости.

delt=0.01 разность конечного и начального значений.

Nt=ceil (delt/tau) число шагов по времени.

d0 11 i=0, Nx задание пространственно-временной сетки.

x (i)=i*h.

11 continue.

d0 12 i=0, Nt.

t (i)=i*tau.

12 continue.

>> do 111 i=0, Nx задание начальных условий.

tab (0,i)=(3*x (i)*(1-x (i)))+0.12.

111 continue.

>> do 112 j=0, Nt матрица граничных условий.

tab (j, 0)=2*(t (j)+0.06).

tab (j, Nx)=0.84.

112 continue.

tab =.

• 0.1200 0.3900 0.6000 0.7500 0.8400 0.8700 0.8400
• 0.1233 0 0 0 0 0 0.8400
• 0.1267 0 0 0 0 0 0.8400
• 0.1300 0 0 0 0 0 0.8400
• 0.1333 0 0 0 0 0 0.8400
• 0.1367 0 0 0 0 0 0.8400
• 0.1400 0 0 0 0 0 0.8400

% заполнение оставшейся части матрицы.

do 114 j=1, Nt.

do 115 i=1, Nx-1.

tab (j, i)=1/6*(tab (j-1,i-1)+4*tab (j-1,i)+tab (j-1,i+1));

• 115 continue;
• 114 continue

tab =.

• 0.1200 0.3900 0.6000 0.7500 0.8400 0.8700 0.8400
• 0.1233 0.3800 0.5900 0.7400 0.8300 0.8600 0.8400
• 0.1267 0.3722 0.5800 0.7300 0.8200 0.8517 0.8400
• 0.1300 0.3659 0.5704 0.7200 0.8103 0.8444 0.8400
• 0.1333 0.3607 0.5612 0.7101 0.8009 0.8380 0.8400
• 0.1367 0.3562 0.5526 0.7004 0.7920 0.8322 0.8400
• 0.1400 0.3524 0.5445 0.6911 0.7834 0.8268 0.8400

% визуализация численного решения (рис 16.1).

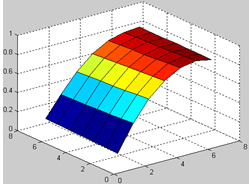
Рис. 16.1. Графическое решение уравнения теплопроводности

Аппроксимация экспериментальных данных Метод наименьших квадратов Идея метода наименьших квадратов (МНК) принадлежит А. Лежандру, а теоретическое обоснование К.Гауссу. В соответствии с этим методом, оценки параметров определяют из условия минимума суммы квадратов отклонений измеренных значений от соответствующей ординаты рассмотренной кривой.

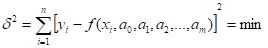
При обработке результатов измерений часто возникает необходимость построить эмпирическую формулу, дающую аналитическое выражение функциональной зависимости, заданной таблицей.

Общепринятым и весьма эффективным при решении подобных задач является так называемый метод наименьших квадратов, при котором требование наилучшего согласования искомой кривой и экспериментальных точек сводится к тому, чтобы «сумма квадратов отклонений» экспериментальных точек от искомой функции обращалась в минимум.

Постановка задачи.

Пусть результаты измерений представлены таблицей.

Если каждое из измеряется несколько раз, то в таблице заменяется средним арифметическим значением данной величины.

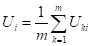
(1).

Далее выбираем общий вид функции, зависящей от нескольких числовых параметров, , именно эти параметры и требуется выбрать согласно методу наименьших квадратов так, чтобы сумма квадратов отклонений от была минимальна. Запишем как функцию не только аргумента, но и параметров, , :

(2).

Требуется выбрать, , так, чтобы выполнялось условие.

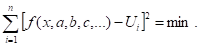
(3).

Замечание:

Следует заметить, что на практике не редко встречаются случаи, когда экспериментальные данные при различных значениях аргумента вследствие каких-либо причин обладают различной точностью. Это имеет место тогда, когда дисперсии неоднородны.

В этом случае необходимо минимизировать взвешенную сумму квадратов отклонений экспериментальных и вычисленных значений функции.

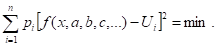
Здесь — веса наблюдений.

Найдем значения, , обращающие левую часть выражения в минимум.

Для этого продифференцируем ее по, , и приравняем производные к нулю:

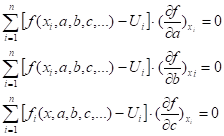
(4).

где.

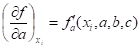
— значение частной производной функции по параметру в точке ,.

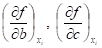
— частные производные по параметрам и искомого функционала.

Решить систему (4) в общем виде нельзя, для этого необходимо задаться конкретным видом функции .

Рассмотрим наиболее часто встречающийся на практике случай, когда является степенным полиномом, т. е.

(5).

Подбор параметров линейной функции методом наименьших квадратов В опыте зарегистрирована совокупность значений, .

Требуется подобрать по методу наименьших квадратов параметры линейной функции,.

(6).

описывающей полученную экспериментальную зависимость.

Для отклонений имеем выражения:

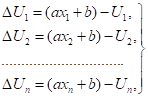
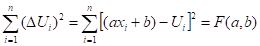
Таким образом, для случая линейного приближения сформулированная в предыдущем параграфе задача сводится к исследованию на экстремум функции двух переменных .

Согласно системе (4), необходимые условия экстремума дают.

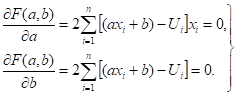
(9).

Поскольку.

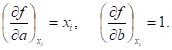
Сокращая на 2, получим систему (9) в виде (4). Далее преобразуем уравнения (9) к виду.

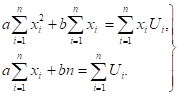
(11).

Решая систему (11), получим.

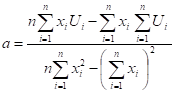
(12).

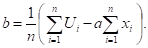
(13).

Определив из выражений (12) и (13) искомые и, мы найдем тем самым искомую эмпирическую формулу в виде (6).

(6).

Теория дает возможность определить также дисперсию отклонения точек от прямой и дисперсию коэффициентов и. Если — дисперсия точек, и — дисперсия коэффициентов и, тогда.

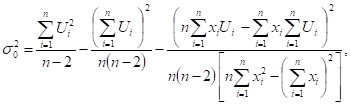
(14).

(15).

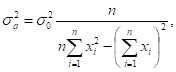
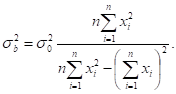
(16).

Примечание:

Далеко не всякая зависимость описывается уравнением прямой линии. Однако в ряде случаев можно путем несложных преобразований привести к линейной более сложную зависимость.

Степенная функция (геометрическая регрессия) Найдем теперь приближающую функцию в виде.

(9).

Предполагая, что в исходной таблице значения аргумента и значения функции положительны, прологарифмируем равенство (9) при условии.

(10).

Так как функция является приближающей для функции, функция будет приближающей для функции. Введем новую переменную, тогда, как следует из (10), будет функцией от: .

Обозначим.

(11).

Теперь равенство (10) принимает вид.

(12),.

т.е. задача свелась к отысканию приближающей функции в виде линейной. Практически для нахождения искомой приближающей функции в виде степенной (при сделанных выше предположениях) необходимо проделать следующее:

• 1) по данной таблице (1) составить новую таблицу, прологарифмировав значения и в исходной таблице;
• 2) по новой таблице найти параметры и приближающей функции вида (12);
• 3) используя обозначения (11), найти значения параметров и и подставить их в выражение (9).

Показательная функция Пусть исходная таблица такова, что приближающую функцию целесообразно искать в виде показательной функции:

(13).

Прологарифмируем равенство (13):

(14).

Приняв обозначения (11), перепишем (14) в виде:

(15).

Таким образом, для нахождения приближающей функции в виде (13) нужно прологарифмировать значения функции в исходной таблице и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы приближающую функцию вида (15). Вслед за этим в соответствии с обозначениями (11) остается получить значения искомых параметров и и подставить их в формулу (13).

Логарифмическая функция Пусть приближающая функция имеет вид:

(16).

Легко видеть, что для перехода к линейной функции достаточно сделать подстановку. Отсюда следует, что для нахождения значений и нужно прологарифмировать значения аргумента в исходной таблице и, рассматривая полученные значения в совокупности с исходными значениями функции, найти для полученной таким образом новой таблицы приближающую функцию в виде линейной. Коэффициенты и найденной функции подставить в формулу (16).

Гипербола Если точечный график, построенный по таблице экспериментальных значений, дает ветвь гиперболы, приближающую функцию можно искать в виде:

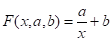
(17).

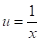
Для перехода к линейной функции сделаем подстановку .

(18).

Практически перед нахождением приближающей функции вида (17) значения аргумента в исходной таблице следует заменить обратными числами и найти для новой таблицы приближающую функцию в виде линейной (18). Полученные значения параметров и подставить в формулу (17).

Подбор параметров параболы второго порядка методом наименьших квадратов В опыте зарегистрированы значения, сведенные в таблицу. Требуется методом наименьших квадратов подобрать параметры квадратичной функции-параболы второго порядка.

(17),.

сoответствующей наблюдаемой экспериментальной зависимости.

Итак, эмпирическую формулу ищем в виде.

(18).

Для отклонений имеем выражения.

(19).

отсюда.

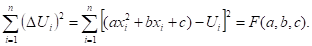
(20).

Необходимые условия экстремума дают.

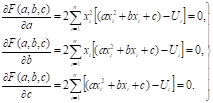
(21).

Систему (21) можно непосредственно записать, исходя из общей системы (4), с учетом того, что.

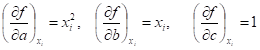
(22).

Аналогично тому, как это сделано в предыдущем параграфе, получим систему нормальных уравнений:

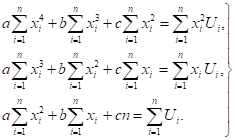
(23).

Решая систему (23), находим искомые коэффициенты и тем самым определяем искомую эмпирическую функцию.

Пример 1. Приближение функции по методу наименьших квадратов.

Пусть функция задана таблицей своих значений:

Приблизим функцию многочленом 2-ой степени. Для этого вычислим коэффициенты нормальной системы уравнений:

Составим нормальную систему наименьших квадратов, которая имеет вид:

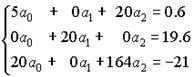
Решение системы легко находится:

Таким образом, многочлен 2-ой степени найден:

Способ наименьших квадратов не может дать ответа на вопрос о том, какого вида функция лучше всего аппроксимирует данные экспериментальные точки.

Вид функции должен быть задан на основании каких-то физических соображений. Метод наименьших квадратов позволяет нам лишь выбрать, какая из прямых, экспонент или парабол является лучшей прямой, лучшей экспонентой или лучшей параболой.

Можно предложить лишь методику определения степени приближающего полинома вида Предположим, что функцию можно с высокой точностью аппроксимировать многочленом некоторой степени. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные содержат случайные ошибки.

Отметим, что широко используемая при полиномиальной аппроксимации система функций.

.

приводящая к классическим алгебраическим многочленам, применяется лишь при. Если, то, как правило, нормальная система уравнений настолько плохо обусловлена, что вычисленные на ее основе параметры оказываются полностью искаженными ошибками округления.

Хорошее сглаживание ошибок эксперимента при среднеквадратичной аппроксимации наблюдается когда. Но если слишком мало, то для описания сложной нелинейной зависимости коэффициентов многочлена может не хватить. Ясно, что в каждом конкретном случае должно существовать какое-то оптимальное число коэффициентов. Определяется оно следующим образом.

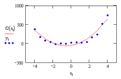
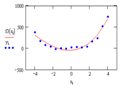
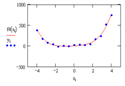
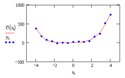
Задавшись некоторым числом и определив согласно (5) соответствующие коэффициенты, вычислим остаточную дисперсию.

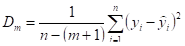
(6).

и сравним ее с известной точностью эксперимента по критерию Фишера.

Применение критерия Фишера Пусть имеются две выборки объемом и соответственно случайных величин и, имеющих нормальное распределение. Необходимо проверить равенство их дисперсий. Статистика теста.

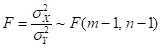
где — дисперсия.

Если вычисленное значение критерия больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными.

Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости и степеней свободы числителя и знаменателя .

Fkp = finv (,) — специальная функция в Матлаб, вызов которой возвращает критическое значение критерия Фишера.

Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n1=32), а для менеджеров 4,41 (n2=33). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05.

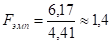
Для ответа на поставленный вопрос определим эмпирическое значение критерия:. При этом критическое значение критерия .

Таким образом,, поэтому гипотеза о равенстве дисперсий на уровне значимости 0,05 принимается.

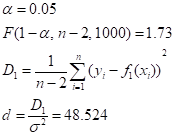
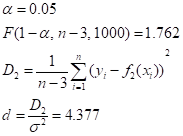
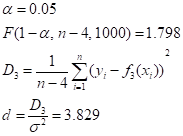
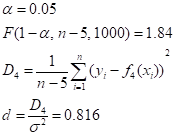
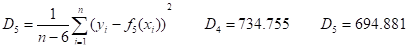
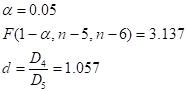
Возвращаясь к нашей задаче, имеем, если.

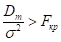
(7).

то математическая погрешность аппроксимации (значимо) больше физической погрешности исходных данных, и формула (5) нуждается в уточнении. Поэтому увеличиваем на единицу, вычисляем по формуле (5) коэффициенты и повторяем проверку качества аппроксимации согласно (6), (7).

Обычно расчет начинают с, когда (при нелинейной зависимости) неравенство (7) заведомо выполнено, и…

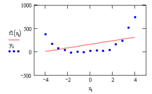
Для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения, с осью абсцисс. Например, пусть есть уравнение Преобразуем его в и определим, что График функции имеет вид.

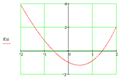
Таким образом, можно приблизительно определять область локализации корней уравнения. Так, видно, что данное уравнение имеет два действительных корня — один на отрезке [-1, 0], а второй — [1, 2].

Пример 1.

Отделить корни трансцендентного уравнения графически.

Решение.

1. Создайте файл Func. m, содержащий описание функции.

Файл Func.m.

function z=Func (x).

z=x.^2-sin (x)-1;

2. Постройте график функции в промежутке [-2; 2], выполнив в командном окне пакета MATLAB следующую последовательность операторов:

>> x= -2:0.1:2;

>> plot (x, Func (x)); grid on.

3. Из рисунка видно, что функция имеет два корня:

х1[-1; 0] и х2 [1; 2].

Пример 2.

Методом половинного деления уменьшить промежуток изоляции корня х2 [1; 2] уравнения до промежутка длиной 0,1.

Метод дихотомии (половинного деления) основан на последовательном делении отрезка локализации корня пополам.

Теорема: Если непрерывная и строго монотонная на отрезке функция на концах его имеет противоположные знаки, т. е., то на интервале имеется один и только один корень.

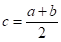
Для реализации этого метода выбирается начальное приближение к отрезку такое, что, затем определяется знак функции в точке — середине отрезка. Если он противоположен знаку функции в точке, то корень локализован на отрезке, если же нет — то на отрезке .

Решение.

1. Создайте файл ChislOtd. m, содержащий описание функции, уменьшающий промежуток изоляции корня методом дихотомии.

Файл ChislOtd.m.

function ChislOtd (f, x1, x2,h);

% f — имя m-файла, содержащего описание функции.

% x1 — левая граница отрезка, на котором производится поиск решения.

% x2 — правая граница отрезка, на котором производится поиск решения.

% h — длина промежутка изоляции корня.

a=x1;

b=x1+h;

while b<=x2.

if feval (f, a)*feval (f, b)<=0.

% feval (f, c) — оператор вычисления в точке х=с значения.

% функции, описание которой находится в соответствующем файле.

% Имя файла хранится в строковой переменной f.

a.

b.

end;

a=b;

b=b+h;

end;

2. Найдите новый промежуток изоляции корня:

>> ChislOtd ('Func', 1,2,0.1).

a =.

1.4000.

b =.

1.5000.

Таким образом, мы получили промежуток изоляции корня.

[1,4; 1,5], который имеет длину 0,1.

ОПРЕДЕЛЕНИЕ КОРНЕЙ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ ЦЕЛЬ РАБОТЫ Привить студентам знания об основных этапах решения уравнения, выработать навыки использования различных методов для уточнения корня уравнения.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ.

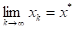
Все численные методы решения уравнений представляют собой алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню и затем с помощью формулы генерируется последовательность сходящаяся к корню уравнения .

Пример 1.

Решить уравнение методом половинного деления с точностью 0,001 (промежуток изоляции корня [1,4; 1,5]).

Решение.

1. Создайте файл Func. m, содержащий описание функции.

Файл Func.m.

function z=Func (x).

z=x.^2-sin (x)-1;

2. Создайте файл Div2. m, содержащий описание функции, возвращающей значение корня уравнения методом половинного деления.

Файл Div2.m.

function Div2(f, x1, x2,esp);

% f — имя m-файла, содержащего описание функции.

% x1 — левая граница отрезка, на котором производится поиск решения.

% x2 — правая граница отрезка, на котором производится поиск решения.

% eps — точность решения.

L=x2-x1;

k=0;

% k — счетчик количества шагов приближения к корню.

while L>esp.

c=(x2+x1)/2;

k=k+1;

if feval (f, c)*feval (f, x1)<0.

% feval (f, c) — оператор вычисления в точке х=с значения.

% функции, описание которой находится в соответствующем файле.

% Имя файла хранится в строковой переменной f.

x2=c;

else.

x1=c;

end;

L=x2-x1;

end;

x=c.

k.

fx=feval (f, c).

% fx — значение невязки.

3. Вычислите значение корня уравнения.

>> Div2('Func', 1.4,1.5,0.001).

x =.

1.4102.

k =.

fx =.

0.0014.

Ответ: решение х=1,4102 мы получили с точностью 0,001 за семь итераций.

При этом значение невязки fx = 0,0014.

Пример 2. Решить уравнение методом итераций с точностью 0,001 (промежуток изоляции корня [1,4; 1,5]).

Метод простой итерации Это простейший из методов нахождения корней. В качестве итерационной формулы используется выражение независимой переменной из исходного уравнения:

Исходное уравнение — путем арифметических преобразований приводится к виду, который может использоваться в качестве итерационной формулы.

Данное преобразование, как правило, не однозначно и совершенно отдельной задачей является оценка применимости и эффективности того или иного способа преобразования.

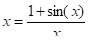
Например, уравнение можно преобразовать, например, так или так или так и т. д.

Задавшись начальным приближением к корню (например, из анализа графика функции или априорных соображений физически реальной модели) можно найти решение:, затем ,…,.

Ниже приведена таблица вычислений для представленных выражений, начиная с одного и того же начального приближения.

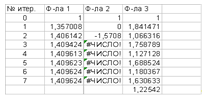
Точность до семи значащих цифр достигается при данном выборе начального приближения для первой итерационной формулы уже на шестом шаге итерационной процедуры, для третьей — на 115-м (в таблице не показано). А вот для второй формулы уже на третьем итерационном шаге вычисления прекращаются, так как под знаком арксинуса оказывается число, большее единицы (нарушается область определения функции).

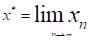
Теорема 3. Пусть функция g (x) определена и дифференцируема на отрезке, причем все ее значения, и существует такое вещественное число q, что, x, то итерационная последовательность сходится независимо от начального приближения и предельное значение является единственным корнем уравнения на отрезке .

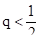
Чем меньше значение q, тем «быстрее» сходится итерационная последовательность. Сходимость будет достаточно «быстрой», если .

Решение.

1. Создайте файл Func. m, содержащий описание функции.

Файл Func.m.

function z=Func (x).

z=x.^2-sin (x)-1;

2. Создайте файл Func1. m, содержащий описание итерационной формулы .

Файл Func1.m.

function y=Func1(x).

y=sqrt (1+sin (x)).

3. Создайте файл Iter. m, содержащий описание функции, возвращающей значение корня уравнения методом итераций.

Файл Iter.m.

function Iter (f, x0, esp).

x1=Func1(x0);

k=1;

while abs (x1-x0)>esp.

x0=x1;

x1=Func1(x0);

k=k+1;

end;

x=x1.

k.

fx=feval (f, x1).

4. Вычислите значение корня уравнения:

>> Iter ('Func', 1.4,0.001).

x =.

1.4076.

k =.

fx =.

— 0.0055.

Ответ: решением уравнения будет число х=1,4076, полученное на 5 шаге. Значение невязки fx = -0.0055.

Решение алгебраических и трансцендентных уравнений в среде MATLAB осуществляется с помощью следующих встроенной функции: fzero ().

Функция fzero () имеет следующую реализацию:

[x, f, e_flag, inform] = fzero ('f (x)', x0).

где:

x — искомое неизвестное;

f — значение невязки;

e_flag — переменная, знак которой свидетельствует о наличии корня на данном интервале (например, e_flag=1 — корень существует);

inform — содержит три поля с именами iterations (количество итераций), funcCount (количество обращений к функции f (x)), и algorithm (наименование алгоритма, использованного для нахождения корня;

'f (x)' - решаемое уравнение, записанное в одиночных кавычках;

x0 — начальное приближение или интервал поиска решения.

Пример 3.

Необходимо найти корни уравнения.

.

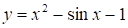
если известно, что корни находятся в промежутках [-1, 0] и [1, 2].

Решение:

>> [x, f, e_flag, inform]=fzero ('x²-sin (x)-1',[-1, 0]).

x =.

— 0.6367.

f =.

e_flag =.

inform =.

iterations: 8.

funcCount: 8.

algorithm: 'bisection, interpolation'.

>> [x, f, e_flag, inform]=fzero ('x²-sin (x)-1',[1, 2]).

x =.

1.4096.

f =.

— 1.1102e-016.

e_flag =.

inform =.

iterations: 10.

funcCount: 10.

algorithm: 'bisection, interpolation'.