Решение треугольника. 
Решение треугольника

Задание

Необходимо решить один сфероидический (сферический) треугольник двумя способами:

• — по теореме Лежандра;
• — способом аддитаментов.

Решение треугольника.

1. По теореме Лежандра

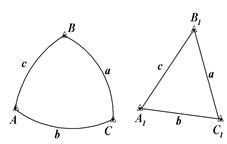
Рис. 1 Схема сферического и прямоугольного треугольников

Исходные данные.

Величину f принимаем по таблице, исходя из заданной средней широте Вm. При вычислении сферического избытка е, длины сторон треугольника выражаются в километрах.

Таблица величины f.

Широта Bm	X, км.
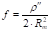40°.	4 430.	0,0025 383.
	4 652.	0,0025 369.
	4 874.	0,0025 357.
	5 096.	0,0025 345.
	5 319.	0,0025 333.
	5 541.	0,0025 322.
	5 763.	0,0025 310.
	5 986.	0,0025 299.
	6 209.	0,0025 287.
	6 431.	0,0025 277.
	6 654.	0,0025 266.
	6 877.	0,0025 256.
	7 100.	0,0025 246.
66°.	7 323.	0,0025 237.

Вычисление сферического избытка.

Решение треугольника.

щ = У — (е + 180°) — угловая невязка треугольника.

Стороны сферического треугольника.

2. Способ аддитаментов

Идея способа аддитаментов заключается в том, что стороны сферического треугольника a, b, c исправляют поправками, в результате чего получают стороны плоского треугольника a', b', c' и неизвестные стороны сферического треугольника.

При этом в логарифмическом варианте, аддитаментами называют поправки в логарифмы сторон A_a, A_b, A_c. В случае нелогарифмического решения, аддитаментами являются величины.

;; ,.

где , — средний радиус кривизны эллипсоида для района расположения треугольника. Значение величины kможно считать постоянной для территории России и равной.

.

при этой размерности k стороны треугольников должны быть выражены в километрах.

Последовательность решения сферического треугольника:

• 1. Из исходной стороны b вычитают её аддитаментA_b и получают сторону плоского треугольника b'.
• 2. По известным углам сферического треугольника и стороне b' решают треугольник как плоский, используя теорему синусов, и находят остальные стороны плоского треугольника a', c'.
• 3. Полученные значения сторон исправляют их аддитаментамиA_a, иA_c и вычисляют искомые стороны a, c сферического треугольника АВС.

Способ аддитаментов применяется как контрольныйпри решении треугольника по теореме Лежандра.

Рабочие формулы.

.

; ;

; ;

; .

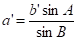
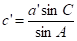
Решение треугольника.

Вывод: В проделанной работе мы решили один сфероидический (сферический) треугольник двумя методами:

• — по теореме Лежандра
• — способом аддитаментов.

В обоих случаях длины сторон сошлись Вычисление длины дуги меридиана Пусть точкаА (рис. 20) на меридианном эллипсе имеет широту В. Возьмём на бесконечно малом расстоянии dX от точки А точку А₁, имеющую широту B + dB; таким образом, разность широт точек А и А_1, соответствующая длине дуги меридиана dX будет dB.

Меридиан представляет собой полуэллипс, концы которого совпадают с полюсами эллипсоида. Экватор делит меридиан на две симметричные части. Рассматривая элементарную дугу dXкак дугу окружности с радиусом М, получаем.

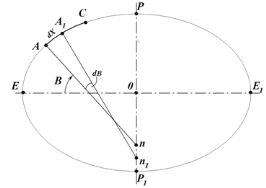
Длина дуги меридиана Следовательно, для вычисления длины дуги меридиана в пределах широт 0 доВ° необходимо найти интеграл:

Этот интеграл является эллиптическим и не выражается в элементарных функциях. Для того чтобы привести его к виду, пригодному для вычисления, необходимо найти его приближённое выражение. С этой целью подынтегральную функцию разложим в ряд, а затем проинтегрируем этот ряд почленно.

С коэффициентами, вычисленными по элементам эллипсоида Красовского, окончательно получим:

По этой формуле длина дуги меридиана вычисляется с ошибкой менее.

0, 0001 м.

С ошибкой не более 0,2 м длину дуги меридиана вычисляют по формуле:

Вычислить длины дуги меридиана между двумя точками с широтами В₂ = 6°40'17,364''и B₁ = 3°20'08,619'', пользуясь формулой Симпсона:

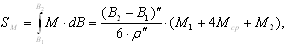
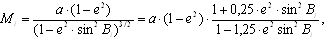
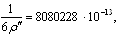
В₁ и В₂ — широты концов дуги меридиана; М₁, М₂, М_ср — значения радиусов кривизны меридиана в точках с данными широтами и с широтой.

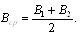
Для контроля вычислений длину дуги меридиана S_М следует вычислить как сумму длин дуг Х₁ и Х₂ меридиана от точки с широтой В_ср до точек с широтами В₁ и В₂. На основании (93) будем иметь (рис. 21).

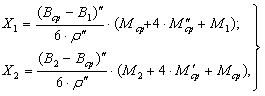
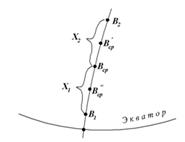
Вычисление длины дуги меридиана где M'_сриM''_ср — значения радиусов кривизны меридиана в точках с широтами.

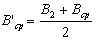
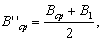
и которые определяются по формуле (94).

Вычисление длины дуги меридиана Схема решения, а = 6 378 245,0 м; e2 = 0,006 69 342.

Таблица 1.

аддитамент сферический треугольник меридиан Контрольное вычисление длины дуги меридиана Схема решения, а =6 378 245,0 м; e2 = 0,006 69 342.