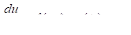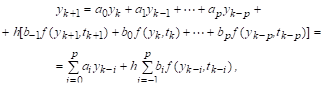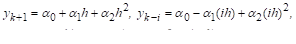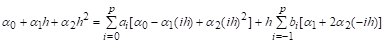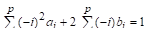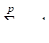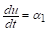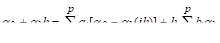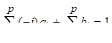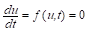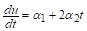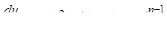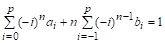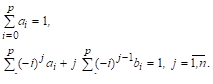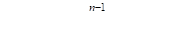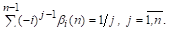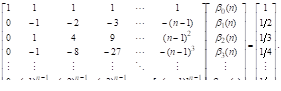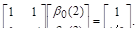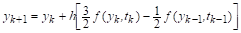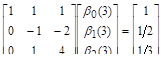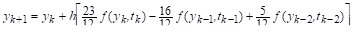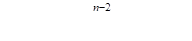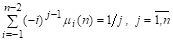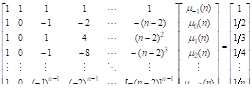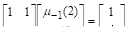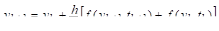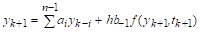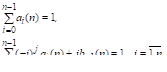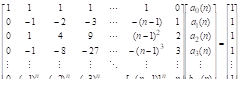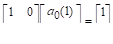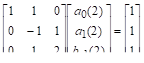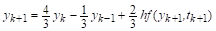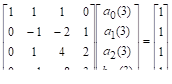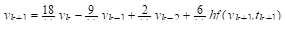Линейные многошаговые методы
Предположим, что построены приближенные значения решения и его первой производной в моменты времени, т. е. Приведем в заключение оценку локальной погрешности (без вывода) метода Гираго порядка: Где константа зависит от порядка метода и для приведенных схем соответственно равна: Общий вид разностной схемы рассматриваемых здесь многошаговых методов имеет вид. Подставив эти значения в разностную… Читать ещё >
Линейные многошаговые методы (реферат, курсовая, диплом, контрольная)
Пусть требуется найти решение на отрезке задачи Коши.
.
Предположим, что построены приближенные значения решения и его первой производной в моменты времени, т. е.
.
Общий вид разностной схемы рассматриваемых здесь многошаговых методов имеет вид.
где — коэффициенты (их всего), которые должны быть определены при получении конкретного многошагового метода, — шаг интегрирования.
Значения этих коэффициентов выбирают так, что если решение является полиномом степени, то разностная схема многошагового метода дает точное значение, т. е.. Поскольку полином степени.
имеет параметр, то разностная схема должна иметь по крайней мере коэффициент. В большинстве практических многошаговых методов и лишние коэффициенты могут быть выбраны произвольно.
Получим соотношения, которым должны удовлетворять все коэффициента разностной схемы в предположении, что метод дает точное решение для задачи Коши, точным решением которой является полином степени. Поскольку полиномй степени включает в себя все полиномы степени ниже, то разностная схема должна также давать точное решение для всех задач Коши, имеющих полиномиальное решение степени меньшей, чем. В частности:
. Класс задач с таким решением задается уравнением.
.
Поэтому.
.
.
.
Подставив эти значения в разностную схему, получим первое ус…
Приведем в заключение оценку локальной погрешности (без вывода) метода Гираго порядка:
.
где константа зависит от порядка метода и для приведенных схем соответственно равна:
.