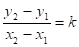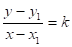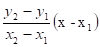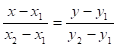Линии первого порядка. 
Прямые на плоскости

Пусть задана декартова система координат и некоторая прямая; б — угол наклона прямой к оси Ох.

Определение: Тангенс угла б наклона прямой к оси Ох называется угловым коэффициентом этой прямой: k = tgб.

= (1).

Формула (1) — определение углового коэффициента по известным двум точкам прямой.

Пусть прямая, неперпендикулярная оси Ох, имеет угловой коэффициент k и отсекает на оси Оу отрезок ОВ= b.

1). Пусть М (х, у) — точка с переменными координатами (переменная точка). Рассмотрим точку В (0, b). По формуле (1) угловой коэффициент равен.

(2).

Преобразуем формулу (2) к виду.

или.

(3).

Если точка М не принадлежит данной прямой, то уравнение (3) не выполнится, следовательно, (3) — это уравнение прямой (по определению).

Уравнение (3) определяет прямую, имеющую угловой коэффициент k, и отсекающую на оси Oу отрезок b, и называется уравнением прямой с угловым коэффициентом.

2). Пусть известна одна точка М₁ (х₁, у₁) и угловой коэффициент k:

По формуле (1), если М (х, у) — переменная точка,.

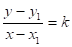
(4).

или.

(5).

Уравнение (5) — это уравнение прямой с угловым коэффициентом k, проходящей через точку М_{1 .}

3) Пусть известны точки М₁ (х₁, у₁) и М₂ (х₂, у₂), принадлежащие прямой. Найти уравнение этой прямой.

По формуле (1) —. Отсюда, с учетом (5), получим.

=.

или, поделив обе части равенства на ,.

. (6).

Уравнение (6) — это уравнение прямой, проходящей через две заданные точки.